Hmm.
Jag håller nog inte riktigt med om Grafpros beskrivning av panel B. Det brukar bli väldigt rörigt om man blandar ihop tids- och frekvensdomänerna.
Jag skulle i stället vilja göra den här beskrivningen:
Att mäta tonkurva är att mäta hur starkt varje frekvens tar sig igenom ett system. Det klassiska sättet att mäta det är med ett sinussvep à la Tombstone. Sinussvepet vandrar ju igenom alla frekvenser och det är bara att se vilken amplitud som signalen får när den har passerat systemet. Man måste dock låta svepet gå långsamt så att det i varje litet ögonblick ser ut som en statisk sinus, så att systemet hinner "svänga in", så att de transienta delarna av svaret hinner klinga av.
Ett annat alternativ är att använda sig av spektrumanalys. Om man matar systemet med en signal som innehåller alla frekvenser (lika starkt), tex vitt brus, så kan man göra en mätning av spektrum på utsignalen och den kommer då att visa tonkurvan. Man kan också mata systemet med en impuls (en väldigt kort och stark "spik") och mäta spektrum på utsignalen på samma sätt. En impuls innehåller likt det vita bruset alla frekvenser och alla frekvenser är lika starka. Skillnaden mellan brus och impuls är att i bruset är fasläget på frekvenserna slumpmässigt, i impulsen är det endast cosinusar med 0 graders fasförskjutning. Det som vill kan prova att lägga ihop 100 cosinusar i excel och se att det blir rätt impulslikt.
Problemet med brusmätning är att bruset är slumpmässigt, och man kommer att behöva medelvärdesbilda över flera perioder om man ska få en stabil tonkurva. LTAS brukar det kallas, och det funkar rätt bra.
Problemet med direkt impulssvarsmätning är att det är väldigt svårt att få någon större energi i en impuls; all energi ligger ju koncentrerad till ett väldigt kort ögonblick.
Då föds tanken att man kan ta en signal, vilken som helst och göra spektralanalys (FFT) både på insignal och utsignal. Då kommer man ju att se för varje frekvens hur den har ändrats i amplitudled och fasled också faktiskt. Och det funkar med vilken signal som helst som innehåller alla frekvenser med en rimligt stor amplitud.
Och om man gör en invers spektralanalys (IFFT) så kan man räkna ut hur impulssvaret (i tidsdomänen) skulle ha sett ut om man hade mätt med en impuls. Det fina med det är att man kan pytsa ut massor med energi över tid, men att den koncentreras i beräkningarna till ett enda ögonblick. SNR ökar dramatiskt.
Det är detta impulssvar som syns i panel B (och delar i panelerna C). I panel A syns "vilkensomhelstsignalen" (som är ett logsvep i Sirp).
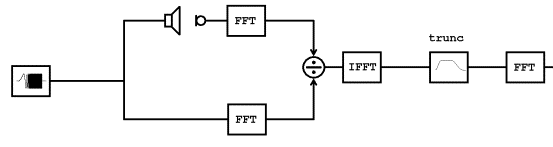
Speciellt intressant som mätsignal är det logaritmiska sinussvepet eftersom det möjliggör mätning av harmonisk distorsion. Detta beror på att distorsionen kommer att följa ett identiskt exponentiellt växande förlopp som grundonen gör. Andratonen kommer att ligga på dubbla frekvensen, eller om man så vill
vara förskjutet till en tidigare tidpunkt. Det är just den exponentiella tillväxten för frekvensen gör att detta inträffar, alltså att man kan se det antingen som en multiplikation i frekvensled eller en förskjutning i tidsled. Resultatet blir, att om det finns dist i systemet så kommer distenergin att koncentreras till en tidpunkt på samma sätt som nyttoenergin, men
tidpunkten ligger tidigare. Detta gör att man kan klippa ut de tidiga delarna av impulssvaret (röd, blå etc i Sirp) och få reda på hur disten beter sig.
Eftersom Sirp vet hur fort svepet går räcker det med att markera huvudimpulsen så kan Sirp beräkna vilka delar som hör till distorsionen.
Dessa delar kan därefter spektralanalyseras (FFT) igen och man får tonkurvan för systemet och distorsionens frekvensberoende. Dessa syns i panelerna D.
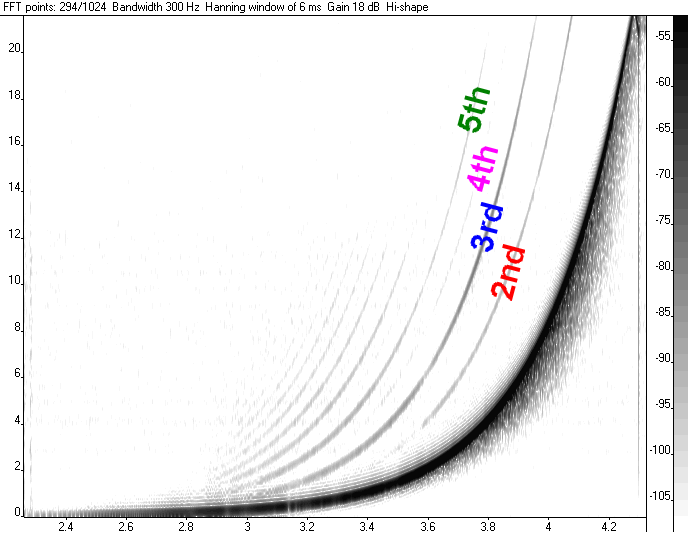
Så, typ, funkar det.
Så länge har jag längat efter att loudness war skulle vara över. Nu börjar jag tro att vi faktiskt är där. Kruxet är att vi förlorade.


