Effekttålighet i basen slutet kontra basreflex

[BPM]

Finns någon skillnad i hur mycket effekt (inte i ljudtrycksnivå nu, där jag begriper att basreflex i är överlägsen till en gräns i basen) mina toppar (2xAura NS3 i 10L) tål innan de slår igenom i sin nuvarande basreflexform jämfört med om jag sluter portarna?

[Nattlorden]

De har inte med effekt att göra som enskilt parameter, det gäller för basreflex var effekten ligger i förhållande till lådans avstämning. Slutna lådor har inte det problemet, men så får de heller inte någon extra boost. Så det är bara att välja...

[BPM]

Avstämningen ligger vid 50Hz (simulerat, ej mätt) och mycket av musiken jag spelar innehåller en hel del information som ligger lägre i frekvens än så.. Har den slutna lådan en fördel under avstämningsfrekvensen? Har för mig jag har hört något sådant nånstans..men vet alltså inte.
Frågan kommer av att jag vill kunna spela musik på hyfsad nivå utan att ha möjlighet att dela dem neråt ett tag..men även se lite film (kommer använda aktiva xtz-subbar i botten via en ofiltrerad pre-out men delade vid antingen 50Hz (med BR-alternativet) eller 80Hz (med slutna alternativet) men alltså utan att dela sidosystemet.. Obs, en nödlösning under en begränsad tid. Jag vet att det inte är optimalt men kommer alltså med den drivningen inte kunna dela sidosystemet så är tvungen) och funderar på vilket av alternativen som bäst klarar en plötslig explosion i en film eller liknande. Med subbarna under så blir det lite svårt att höra när det säger ifrån.

Effekttåligheten borde väl vara densamma så jag lurar mest på konutslagen. Slår elementen i en sluten låda mindre vid, säg 30Hz, än vad de skulle göra i samma låda avstämd till 50Hz?

[Svante]

Finns någon skillnad i hur mycket effekt (inte i ljudtrycksnivå nu, där jag begriper att basreflex i är överlägsen till en gräns i basen) mina toppar (2xAura NS3 i 10L) tål innan de slår igenom i sin nuvarande basreflexform jämfört med om jag sluter portarna?

Jag tror att frågan är krångligare än du tror. Det finns flera olika begränsningar för hur stark signal man kan skicka till en högtalare, en av dem är att det blir varmt i talspolen. En annan är att konamplituden inte får bli för stor. Det är framför allt den senare som basreflexsystemet hanterar; konamplituden blir lägre för sammma utnivå.

Den termiska effekten är dock knepigare. Det är i allt väsentligt strömmen genom talspolen som alstrar värme. Effekten P=I²*Re. Hur stor strömmen blir beror på förstärkarens utspänning och högtalarsystemets impedans Z. Z är frekvenseberoende och olika för slutet resp. basreflex. Effekten som utvecklas i talspolen är för många frekvenser mycket mindre än förstärkarens maximala uteffekt. En förstärkare på 500 W (8 ohm) lämnar bara maximalt 100 W om högtalaren har en impedanstopp på 40 ohm. Förstärkare har ju typiskt en maximal spänning U, som det är brukligt att räkna om till "åttaohmswatt". Och tillsammans med den frekvensberoende impedansen och I=U/Z blir det otrivialt.

Men jag undrar om din fråga inte egentligen är vilket av de två systemen som tål kraftigast förstärkare, alltså egentligen vilket som tål mest spänning.

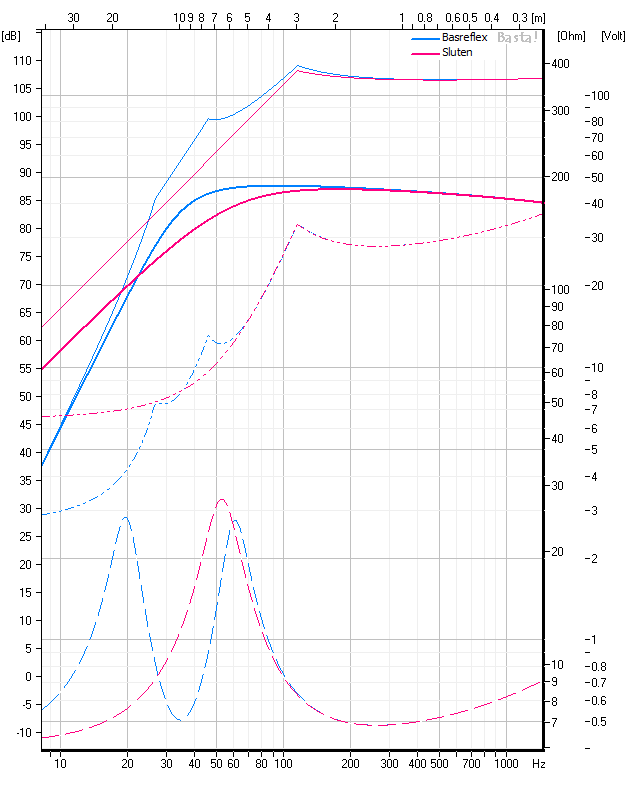
Svaret är att det beror på frekvens. Jag gjorde en liten simulering med Basta!s defaultsystem, där jag pluggade porten. Kurvorna som visas är, nerifrån: Impedans, spänning vid max utnivå, tonkurva och max utnivå. För det slutna systemet begränsas den maximala utnivån av konutslaget under c:a 110 Hz och av värmeutvecklingen däröver. Basreflexen är likadan med skillnaden att den begränsas också termiskt mellan 25 och 45 Hz. Den har ju betydligt lägre konamplitud runt helmholtsresonansen. Maximal spänning blir lite högre för basreflexen över 35 Hz (där helmholtzresonansen ligger), men lägre under.

Ovanstående innehåller en hel del "förståelseapproximationer".

[BPM]

Tack för hjälpen! Mycket intressant, och jag tror att basreflex ändå är vägen att gå då. Skillnaden förefaller så stor med basreflex att den lilla skillnaden under runt 35Hz knappast är värd att offra den större kapaciteten vid en basreflexlösning. Jag kör BR.

[Nattlorden]

Tack för hjälpen! Mycket intressant, och jag tror att basreflex ändå är vägen att gå då. Skillnaden förefaller så stor med basreflex att den lilla skillnaden under runt 35Hz knappast är värd att offra den större kapaciteten vid en basreflexlösning. Jag kör BR.

Det är det ena tankesättet. Det andra är att eftersom slutet är överlägset under 23Hz, så är det slutet som gäller, men man får skaffa fler om nivån inte räcker till.

[Kronkan]

Svante intressanta diagram!

Åsså kommer min standardkommentar. Rummet ger ju också en respons. Min resa för att få till en bas som var möjlig att leva med startade med att jag pluggade portarna på mina ML Purity. Efter en flyttning så blev basen bumlig och ovacker. Första mätningen visade kraftigt höjda nivåer i basområdet. Men minskad nivå under 30 Hz.

Så då pluggade jag portarna. Vill minnas att det blev 3 dB bättre (lägre) i det bumliga området. Detta var för 5 år sedan. Därefter stegvis olika typer av åtgärder. Eftersom jag har en öppen planlösning blev det fler rumsåtgärder för att minska energin i området över 30 Hz som ledde till en ökning av nivån under 30 Hz. Så jag rättade ut kurvan. Ett extremt exempel och lite tjatigt att jag nämner det igen.

Efter att ökat absortionen så provade jag i veckan att ta bort pluggarna men det blev inte bra utifrån en ren subjektiv bedömning.

[BPM]

Tack för hjälpen! Mycket intressant, och jag tror att basreflex ändå är vägen att gå då. Skillnaden förefaller så stor med basreflex att den lilla skillnaden under runt 35Hz knappast är värd att offra den större kapaciteten vid en basreflexlösning. Jag kör BR.

Det är det ena tankesättet. Det andra är att eftersom slutet är överlägset under 23Hz, så är det slutet som gäller, men man får skaffa fler om nivån inte räcker till.

Jag får väl helt enkelt testa lite.. Nu, under den knappa månad det handlar om, så kommer alltså subwoofers (inga värstingar.. "köpesubbar"..huga..) att spela den djupa basen och vid närmare eftertanke tror jag att jag får en snyggare samverkan med topparna slutna och även ett mer kraftfullt totalljud om jag kör slutet och släpper upp delningen mot 70-80Hz jämfört med att köra BR och tvingas dela vid 50Hz (skulle i det läget helst dela djupare men 50Hz är lägsta möjliga på de inbyggda sub-stegen..) då jag vill ha så lite överlapp som möjligt.
Kanske tål de små Aura-elementen mer än jag tror ofiltrerade. Slaglängden är ju minst sagt extrem för storleken..