Fördröjningar i rör

[Svante]

Ja nu tror jag att jag får utfärda en teknikvarning, trots att detta är i teknikforum .

Kanske är det inte ens lämpligt i ett hififorum, men det gäller i alla fall akustik, det har med rör och resonanser att göra så jag tar mig friheten att prova.

Jag har länge brottats med ett problem, som jag tycker att jag förstår på två olika sätt. Det knepiga är att resultatet av de två olika sätten är olika.

Jag har ställt frågan på andra fora och stämde till och med träff med en riktig filterexpert på KTH, men jag har ändå inte lyckats få en förklaring till var jag tänker fel. Så här:

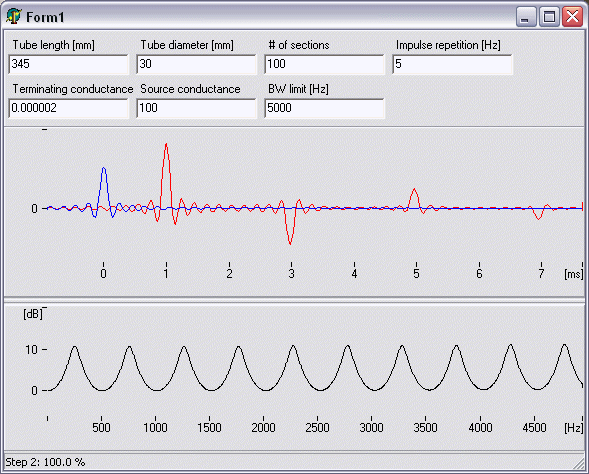
Om man tar sig en rörstump med en källa i ena ändan, kan man modellera den med en LCLCLCL-länk. Ju fler sektioner man tar, desto högre upp i frekvens ger den riktiga resultat.



Överföringsfunktionen för en sådan länk är H(s)=1/Pn(s), dvs ett genom ett n-tegradpolynom i Laplace-s:et, vilket betyder att systemet bara har poler. Överföringsfunktionen kommer snyggt och prydligt att få toppar vid rörresonanserna, om källändan av röret betraktas som sluten och den andra öppen hamnar de vid de frekvenser som motsvarar 1/4, 3/4, 5/4, 7/4 etc våglängder längs rörets längd.
Detta säger mig att modellen är utmärkt på att simulera röret, inklusive löptiden för vågen, eftersom resonansfrekvenserna blir rätt. Man kan också välja att avsluta röret med en resistans om man vill, men det blir fortfarande bara poler i överföringsfunktionen.

Nå, om nu systemet innehåller bara poler, då kan man välan konstruera ett inversfilter som innehåller bara nollställen? Typ I(s)=Pn(s). Kopplar man dessa filter efter varandra borde man få tillbaka signalen som man stoppade in i röret? Hela överföringsfunktionen blir ju nu G(s)=H(s)*I(s)=Pn(s)/Pn(s)=1. Det här är ett vanligt trick man använder inom röstforskning, när man vill se hur luftflödet mellan stämbanden ser ut. Man inversar bort effkten av talröret.

Men...

I verkliga livet är signalen ut från inversfiltret fördröjd med motsvarande löptiden i talröret. Kopplar man på inversfiltret på filtermodellen, blir överföringsfunktionen 1, dvs utan fördröjning. Men modellen var ju bra och modellerade ju fördröjningen OK!

Till att börja med: Förstår ni motsättningen?
Och: har någon en lösning?

[Isidor]

Ja, detta är en närmast klassisk paradox. Kausalitet inom signalanalys kan vara ganska knepigt och vid all filteranalys får man se upp med matematiken eftersom man annars lätt får icke-kausala system. Verkan före orsak känns ju en aning skumt i detta universum åtminstone...

Till att börja med finns det ingenting att invända mot den metod du använder för att simulera vågutbredningen i röret. Det är en form av finit elementmodell och ger som sådan korrekta resultat både i tids- och frekvensplanet så länge som den spatiella upplösningen är tillräckligt hög och vi bara tittar på plana vågor (under den s.k. cut-on-frekvensen där tvärgående moder uppstår i röret). Eftersom jag har en mer mekanisk bakgrund skulle jag i och för sig hellre kunna tänka mig massor, fjädrar och dämpare istället för de elektriska analogierna, men som bekant spelar ju detta ingen roll i slutänden.

Sedan kommer vi till detta med invers filtrering. Egentligen inför man här bara en invers fördröjning som komplementerar fördröjningen i röret så att den totala fördröjningen blir konstant (frekvensoberoende) och ungefär lika med den maximala fördröjningen i röret. Systemfördröjningen efter inversfiltrering blir alltså naturligtvis inte noll, vilket en direkt matematisk analys ger vid handen när man multiplicerar överföringsfunktionerna, utan ökar alltså markant i nästan hela det aktuella frekvensområdet.

Det är alltså tillåtet att titta på systemegenskaperna när det gäller frekvensplanet, men när det gäller tidsplanet och fördröjning måste man titta på delsystemen separat och summera respektive bidrag för att beräkna den totala fördröjningen.

[Svante]

Tack Isidor jag hoppades på svar från dig.

Men... Nu rycker du undan fötterna för mig... Eller kanske är det mitt problem som redan gjort det.

Nog är väl "att titta" i frekvens- respektive tidsdomänen bara två synsätt, det ändrar ingenting i den fysiska verkligheten, väl? Så länge man har med både amplitud och fas i frekvensdomänen så säger de väl samma sak som i tidsdomänen?

Om man skriver överföringsfunktionen som ett polynom á la Laplace, kan man ju tänka i tidsdomänen, med transienta förlopp och allt också, eller hur? Och att multiplicera med inversfunktionen, är det inte OK???

I annat fall skulle ju inte analogin (med tillräckligt många länkar) fånga allt i verkligheten? I såna fall skulle självaste härledningen till vågekvationen var i fara...

Jag inser att det är svårt att tala om fördröjning i fallet när inte vågformen bibehålls (som efter röret med öppen ände), det närmaste är väl grupplöptid, men den är inte hemskt användbar. Om man däremot avslutar röret rätt (så att det inte blir någon reflexion vid mynningen), blir det lättare, för då blir röret just en fördröjning. Fortfarande är modellen minimum-fas (eftersom den bara har poler) och inversen blir därmed stabil och kausal. Där hör jag mig själv säga en motsägelse, inversen till en fördröjning skulle vara kausal... Men eftersom röret kan modelleras med ett all-pol-nät så måste det ju gå. Arrghh...

Förlåt om jag är svårövertygad, men jag måste förstå för att bli övertygad

[Wolfie]

Tidsfördröjningar inom polynom kan ibland ge upphov till en väldans massa funderingar...
Gör man samtidigt en multiplikation (i frekvensdomän) med en inversfunktion så måste man verkligen se upp om/när man bryter loss tidsfördröjningarna...

[Svante]

Tidsfördröjningar inom polynom kan ibland ge upphov till en väldans massa funderingar...
Gör man samtidigt en multiplikation (i frekvensdomän) med en inversfunktion så måste man verkligen se upp om/när man bryter loss tidsfördröjningarna...

Jo... Det är väl kanske det jag råkat ut för. Nu kan jag tycka att jag inte bundit upp mig till frekvensdomänen någonstans. Visserligen använder jag laplacetransform för att förstå att inversfiltret borde "ta ut" röret, men ändå. Tar de ut varann i frekvensdomänen borde de ju göra det i tidsdomänen också.

Just nu lutar jag åt att diskretiseringen av röret i stumpar med längd>0 bara funkar för låga frekvenser, och att impulsen man skickar in därmed måste vara bandbegränsad. En bandbegränsad impuls ripplar innan huvudpulsen kommer och det kunde vara tillräckligt för att ett inversfilter skulle kunna åstadkomma en utpuls innan inpulsen (-s huvudpuls) kommer. Det knepiga med det är att min praktiska erfarenhet av (tal-)rör och inversfilter säger mig att fördröjningen blir kvar.

Jag gjorde en simulering av ett rör med 100 stumpar, och det förefaller tydligt för mig att LCLCLCL-modellen verkligen simulerar fördröjningen. Men det behövs att cutoff-frekvensen ligger en rätt bra bit över bandbegränsningen för att utpulsen ska se ut som inpulsen. Kul att se är också att om inte röret är "riktigt" terminerat får man sekundära pulser, som vandrat tillbaka och reflekterats vid källan.

[Morello]

Svante,

Problemet är ju att det inte går att implementera filter där täljarpolynomet är av högre ordning än nämnarpolynomet.
Ett sådant filter skulle ha oändlig bandbredd, vilket intuitivt är orimligt. Dessutom måste man våldföra sig på Paley-Wieners teorem för att realisera ett sådant filter (med högre ordning i täljare är nämnare).

[Svante]

Svante,

Problemet är ju att det inte går att implementera filter där täljarpolynomet är av högre ordning än nämnarpolynomet.
Ett sådant filter skulle ha oändlig bandbredd, vilket intuitivt är orimligt. Dessutom måste man våldföra sig på Paley-Wieners teorem för att realisera ett sådant filter (med högre ordning i täljare är nämnare).

Jo, jag har tänkt på det, men det "löser" man genom att slänga dit ett nytt nämnarpolynom i inversen, med samma ordning som täljarpolynomet. Detta kan få representera ett system med kortare fördröjning än det ursprungliga. Netto blir då det nya polynomet, som man är fri att välja till vad som helst, tex en rörstump på 0,001 mm.

Så frågan kvarstår.