Jag har en tonkurva som kommer från en FFT. Frekvensaxeln är alltså linjär.
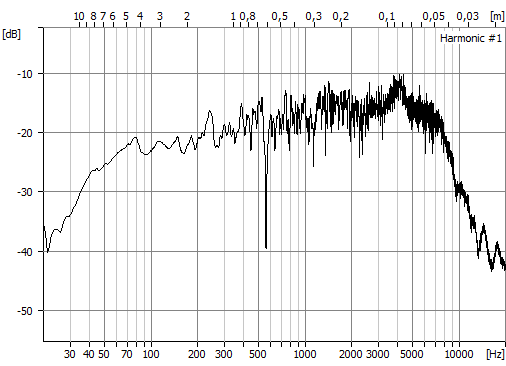
Typiskt blir då kurvan ganska snäll vid låga frekvenser men fladdrar väldigt mycket upp och ner vid höga frekvenser. På gamla kurvskrivarnas tid var detta inget problem, man begränsade ju skrivhastigheten och eftersom man hade logsvep så blev kurvan mer utjämnad vid höga frekvenser än vid låga.
Lösningen som jag har just nu består av ett glättningsfilter med variabel fönsterbredd. För varje mätpunkt lägger jag ett hanningfönster ("raised cosine") på ett område som är tex 1/12 oktav brett kring mätpunkten. Därefter medelvärdesbildar jag över fönstret och får på så sätt ett nytt glättat värde för varje mätpunkt. Resultatet blir så här:
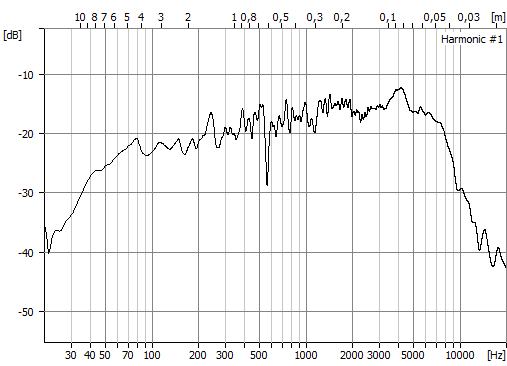
Ganska snyggt, men just den här medelvärdesbildningen, med en 65536-punkters FFT tog 17 sekunder att göra. Det är på tok för långsamt. Man kan iofs förstå att det tar lång tid, jag beräknar ju ett nytt fönster för varje punkt, dvs uppe i diskanten blir det massor med cosinusar och summeringar att göra för varje mätpunkt.
Att försöka sig på 1/3 eller 1/1-oktavbredd är inte att tänka på.
Så: Min fråga är om det finns nåt sätt att snabba upp det här. Det som är knepigt är att filtret behöver innesluta olika många punkter vid olika frekvenser, så jag kommer inte på nåt.
Förslag?
