silverminken skrev:Innebär massan i porten luftens massa i porten? I så fall borde ju resonansfrekvensen sjunka vid ökad rördimater vilket inte är fallet? Så jag antar att massan definieras på annat sätt...
Det är den akustiska massan som avses. Om man utgår från att massan ska lagra rörelseenergi så är det lättare att inse relationerna.
Minskad diameter (area) ökar flödeshastigheten (vid konstant luftpumpning) portionellt.
Aport~1/Vport (där A är portarea och V är hastigheten i porten)
Nu är det rörelseenergin vi är ute efter och den är proportionell mot kvadraten på hastigheten. Då får vi
Wk~1/Aport^2 (Wk är kinetiska energin)
Dessutom är luftmassan direkt proportionell mot längden på röret.
Wk~lp/Aport^2 (lp är längden på porten)
Det är här vi får grunden till den formel som anger den ekvivalenta akustiska massan för porten (som jag tyvärr inte har i huvudet).
Ma~lp/Aport^2 (Ma är den akustiska massan)
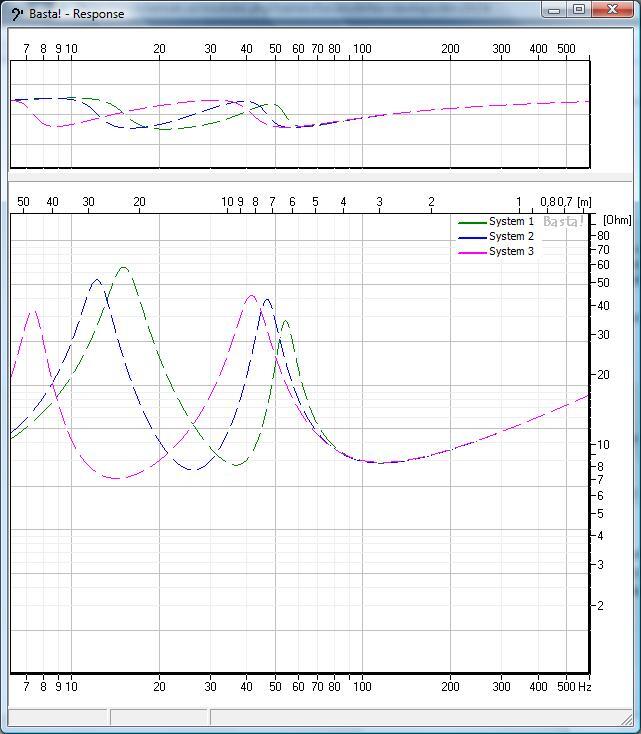
silverminken skrev:Så vid övre toppen har elementet ett rörelsemaxima och luften i porten står ganska still. Vid den undre har porten och elementet tillsammans ett rörelsemaxima? Innebär det att elementet och porten spelar 180 grader ur fas vid den nedre toppen och hyfsat i fas vid helmholzresonansen, eller är jag ute och cyklar?
Element och port spelar bara ur fas vid helholtzresonansen. Vid de övriga resonanserna så får man kolla på fasläget i simuleringsprogrammet.
Man kan därför enkelt se på en impedanskurva hur väl anpassad avstämningen är till elementet.
Tänker du med avseende på elementets slaglängd? Du får gärna utveckla resonemanget om du har tid.
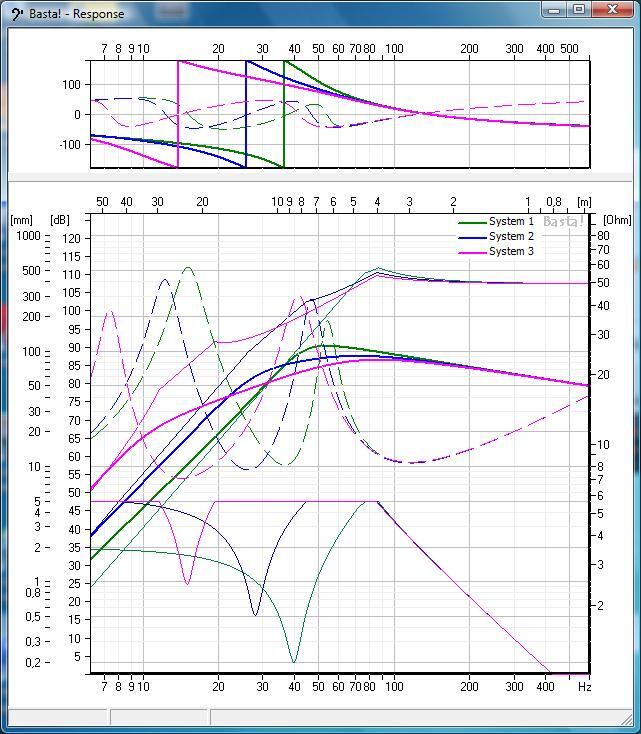
Nja jag tänker mer tt man kan se om man har lite inoptimalt använt realtivt slaglängdsområde. Avstämmer man exempelvis lite för långt ner så dämpas den nedre impedanstoppen och den övre kan öka i förhållande till hur mycket ljudtryck som alstras. Det gör att man kan få genomslag lättare. Men detta ser man lätt i Svantes program Basta! Bara att labba lite.