Okej - filter utan svår matematik, med avsikt att ge läsarna någon sorts
förståelse för vad som händer...
Jag skall göra ett försök, även om jag nog tycker att det som redan sagts
av Almen, Svante och några till om värdet av att lära sig på riktigt, är stort,
och att mitt huvudråd till de jag ser (flera) som slår ifrån sig och antyder
att det är ettpedagogiskt problem att det inte finns en enkel förklaring

är att lära sig på riktigt istället för att lära sig förenklade bilder.
Men härnedan skall jag alltså försöka skiva saker som inte är förenklade till
felaktighet - även om det är strippat på praktiskt taget all matematik.
- - -
För samtidigt som en mera komplett bild förstås är en mycket bättre väg
att gå så är det ju lite av en utmaning att förklara något som är väldigt
komplicerat utan att använde något matematik eller några formler...
Det får mig osökt att tänka på boken 'A Brief History of Time' av Stephen
Hawking, där han går igenom saker som självaste Big Bang, lite om rumtid
och svarta hål. Tunga ämnen onekligen.
Men, egentligen går han inte speciellt djupt alls, och dessutom inkluderar
han faktiskt en ekvation i boken!

Frågan är om en förståelse så ytlig som den som förmedlas i boken, fast
nu då om delningsfilter, skulle vara av värde alls?
Delningsfilter är ju inte mera komplexa än svarta hål, men de är mycket
mera komplicerade saker, än det som
förmedlas om svarta hål, i boken.
Och dessutom tänker jag ju inte skriva någon bok utan bara göra ett litet
inlägg här på faktiskt. Det gör det ännu svårare att åstadkomma en på
något sätt meningsfull text.
Nåja, om det jag skriver härnedan är till någon mening eller nytta för er,
det får ni avgöra själv. Nu vet ni begränsningarna i varje fall.
Jag kommer hur som helt att kopiera ännu en sak ur boken, nämligen att
inkludera en (säger en) ekvation - för den är så grundläggande att man
utan att förstå den på i varje fall basal nivå alls, inte rimligen kan förstå
knappt något som är sant och relevant om delningsfilter sätt att arbeta
alls.
Ohms lag.
- - -
Jag börjar dock med att ta avstånd ifrån en väldigt dålig modell:
En dålig men vanlig förklaring säger att kondensatorer är snabba, och släp-
per igen snabba förlopp - läs höga frekvenser. Spolar däremot sägs vara
långsamma och släpper igenom långsamma förlopp...
Om man utgår ifrån detta men rättar till tossigheten om "snabbhet" till
något med fysikalisk förankring, och sedan adderar ohms lag - den mest
fundamentala för att man alls skall kunna förstå en spänningsdelare (och i
det här fallet även en sådan som inkluderar ett frekvensberoende), så kan
det bli något i den här stilen:
- - -
KAPITEL 1 - ohms lag:
U = I*R
U är spänning, vilket är en sorts elektrisk kraft som vill driva en ström fram-
åt. R är en sorts strömbroms. Ju mera R man har, desto svårare är det att
driva fram en givet ström, eller med andra ord; desto mera spänning (U)
behövs för att driva en given ström. Man kan även från samma ekvation
konstatera att om det går en given ström i en kabel och man ligger ett
motstånd i vägen för strömmen, så kommer att spänning (ungefär som en
tryckskillnad) att falla över motståndet.
Ekvationen kan stuvas om på flera olika sätt utan att vara en ny ekvation.
Exempelvis kan man se att I = U/R. Det vill säga den ström som går genom
en resistans är proportionell mot den spänning som ligger över den, men
även omvänt proportionell mot resistansens storlek. En större resistans/
/ett större motstånd betyder att mindre ström rinner igenom det.
Det tredje sättet att stuva ekvationen är: R = U/I. När den är stuvas så
så berättar den vilket motstånd som föreligger när det uppstår ett visst
spänningsfall av en viss ström.
KAPITEL 2 - Spänningsdelaren.
Nästa steg för förståelsen av filter är att tänka sig en ström som passerar
två motstånd kopplade i serie med varandra. Vi kan för enkelhetens skull
säga att de är lika stora de två motstånden, låt oss säga att de är på 42
ohm vardera. Då kommer "trycket", alltså spänningen som faller över dem
tilsammans att vara U = I*R = I*84, medan den spänning som faller över
bara ett av motstånden blir I*42, hälften så mycket. Så om det ligger 1
volt över dem, som ligger det en halv volt över vart och ett av motstånden.
Vi ar gjort en spänningsdelare med delningstalet 1/2 eller 0,5! Man kan
även kalla det 42/(42'42).
- - -
KAPTIEL 3 - Trögheterna.
Som jag inledde med så är inte spolar tröga och kondensatorer snabba.
De är båda tröga!


Så hur skall man då kunna skilja mellan höga och låga frekvenser?
Jo saken är den, att spolar är strömtröga och kondensatorer är spännings-
tröga. Och det finns förstås fysikaliska orsaker till att det är så. Jag hade
från början tänkt att skippa dem, men jag tror att det kanske är enklare
att bilda sig en rimlig känsla för vad som händer i komponenterna om man
vet lite om de inre mekanismerna, så jag ångrade mig och tänker säga
några ord om saken.
- - -
3A - Spolen.
För att förstå en spole måste man nog börja med att säga några ord om
ett fysikaliskt fenomen som är viktigt för att man skall förstå sig på ladd-
ningar i rörelse.
Jag misstänker att alla har sett bilder av kollisionsprodukter från världens
alla stora partikelacceleratorer. Det är lite klotterliknande streck, som kan
vara oändligt eller ändligt långa raka och krokiga streck med konstant eller
avtagande radier:
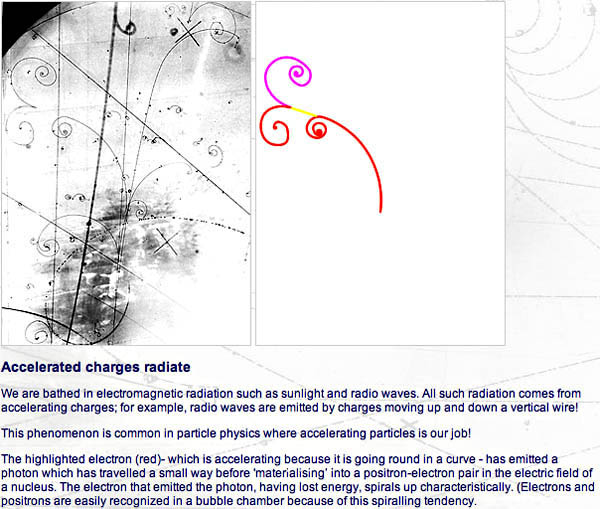
De spår som beskriver raka linjer visar oladdade partiklar eller kluster av
partiklar. Det som går i böjda banor är laddat. krökens riktning (med/mot-
urs) beror på laddningens polaritet. Ju större radie desto tyngre partikel
eller kluster, eller lägre laddning, eller lägre rörelseenergi. Om kröken blir
snävare så visar det att det förloras energi. Och vad beror nu allt detta
på?
Jo, när en laddning rör sig så bildas ett magnetfält runt laddningen (axeln
är i rörelseriktningen) och om det även finns ett statiskt magnetfält till-
städes, tvärs den linje längs vilken laddningen flyger fram så adderas de
på en sida men subtraheras på den andra - det blir ju det en magnetener-
giförtätning på den ena sidan av den, och en förtunning på den andra.
Förtätningen bildar ett "magnetiskt tryck" som vill accelerera laddningen
åt sidan. Flyger laddningen fritt så kommer den att börja svänga med en
radie som beror på dess massa och på dess rörelseenergi. Om rörelse-
energi förloras så blir den en krympande spiral.
Om en laddning rör sig i en tråd så är ofta möjligheten till rörelse dock
oftast begränsad, men "viljan" att röra sig finns kvar - och det finns ett
namn för den fysikaliska tendensen att vilja röra sig - kraft.

Men läxan idag är inte att sätta sig in i denna dynamik (som däremot är av
stor vikt att förstå för den som vill konstruera även högtalarelement). Men
nu är det bara en sak som ni behöver ta fasta på - att en laddning som rör
sig bildar ett cirkulerande magnetfält runt sig. Detta gäller både för fria
laddningar och sådana som är instängda i en ledning, och det är ett linjärt
fenomen - ett magnetfält som blir dubbelt så stort om en dubbelt så stor
ström passerar ledningen.
Så om även då två ledningar löper parallellt med strömmen X genom varje,
kommer magnetfältet som roterar kring dem båda att bli samma som om
strömmen 2*X passerat en ensam ledning.
Innan jag skriver något mera om hur magnetfälten adderas när ledningar går
parallellt vill jag dock belysa en viktigare sak - att energi är oförstörbar,
och att ingen energi kan skapas utan energiskuld. Så den magnetiska energi
som uppehåller sig runt en ledning igenom vilken det går en given ström
(DC, nota bene) måste komma någonstans ifrån. Den "stals" i själva verket
från den yttre energikälla som driver strömmen, i strömmens allra tidigaste
skede - det vill säga när man slöt kretsen.
Även om spolen har mycket låg resistans således att det behövs väldigt
lite spänning för att driva en ström genom den, så behövs mera spänning
för att ÖKA strömmen genom ledningen, ty att öka strömmen betyder
även att man ökar på den energi som fångats i magnetfältet.
Detta fenomen att det går åt energi för att
ändra strömmen genom
en ledning, kan även beskrivas som att en ledning är strömtrög.
(Om man har en ledning helt utan resistans (supraledande) gör strömtrög-
heten att man får en evigt gående ström om man i ett givet ögonblick
sluter en ledning (gör en loop) som det går ström igenom. Och av ström-
men så bildas även evigt "fastlåsta magnetlinjer". Evig så länge som som
vi har supraledning vill säga. Det är därför en supraledande magnetiskt
material kan hållas "flytande" i ett magnetfält. Normala ledningsmaterial
man bara bromsas av kraftiga megnetfält.)
Så - för att ändra strömmen genom en ledning så går det åt elektromot-
orisk kraft (EMK, mäts i volt) Mer och mer ju större induktansen för led-
ningen är. Och om man lindar en ledning (obs; en ledning, inte en kabel
med två poler) många varv så blir ledningen "parallell med sig själv", och
effekten av magnetfältet runt ledningen ökar då varje varv förstärker det
samlade magnetfältet.
Eftersom återverkan från det magnetfält som omger EN ledning (EMK från
uppbrytning eller uppbyggnad av fältet*) nu verkar på alla spolens varv så
växer en kabels induktans med kvadraten på antalet varv. Dubblar man
antalet varv så blir både längden av tråden med fält runt sig dubblad, men
fältet runt varje punkt av ledningen dubblas också. Så spolen växer med
kvadraten på antalat varv (allt annat lika) - ju fler varv man lindar en
spole med en givet storlek, desto större (mätt i Henry) blir spolen, om
växten sker kvadratiskt.
Jo, det skall väl sägas en sak till - att ström ger magnetfält och ändrad
ström betyder ett energiutbyte med magnetfältet (det kan både ta och
ge) är bara halva sanningen. Ändrat magnetfält ger en strömändringskraft
också, och det är så det hela hänger samman, och för att inte komplicera
saken i onödan så skal jag väl säga att det finns en massa olika tänkbara
versioner av det hela (som representerar olika elektriska och elektromekan-
iska system) där saker beter sig en del olika om krafterna tillåts skapa rör-
elser - och om de inte tillåts göra det**.
Spolens induktans berättar om dess strömtröghet - alltså lite förenklat hur
länge en spänning behöver ligga över den för att ändra strömmen genom
den 1 ampere. (Eller om hur stor spänningen behöver vara, lång tid eller
en stor spänning går lika bra - det handlar om produkten mellan de tu.)
- - -
3B - Kondensatorn.
Kondensator är också trög, påstod jag. Men spänningströg. Och vad beror
nu det på då?
För att kunna förstå det måste man nog börja med att titta på ett annat
fysikaliskt fenomen än magnetism och magnetiska krafter, nämligen elektro-
statiska krafter. Laddningar påverkar inte bara varandra när de är i rörelse
(som spolen) utan också när de är i vila. Men då utan att några magnet-
iska fenomen är inblandade.
En sak till man kanske skall nämna är hur en kondensator är uppbyggd.
Svaret på den frågan är att en kondensator är två ledande folier (eller
liknande) kopplade till varsin pol, åtskilda av ett isolerande skikt. Ju större
ytor folierna har, desto mera laddning behövs för att fylla kondensatorn till
en viss spänning, och detsamma gäller för när folierna åtskilj av ett väldigt
tunt isolerande skikt.
Ju tunnare desto mera behöver man fylla kondensatorn med laddningar
för att en given spännining skall finnas mellan plattorna (= benen på kon-
densatorn, för de är kopplade till varandra, men en ledning som förhopp-
ningsvis inte har för stor induktans***)
Men åter till den elektrostatiska krafterna.
Den enkla lagen om detta, säger att motsatser attraherar varandra. Positiva
laddningar vill vara nära negativa laddningar. Men här kommer det viktig-
aste:
Ju mera man drar isär en positiv laddning från en negativ - desto större
spänning uppstår. Inte kraft, men spänning. Det kanske kan vara svårt att
förstå varför och hålla isär dem, men nu var det ju en förenklad beskrivning
som efterlystes, så...

Men en liten parallell skall jag ändå erbjuda. Om man tänker sig en bil som
man puttar upp för en väldigt brant backe så tror jag de flesta förstår att
det är jobbigt att putta upp bilen när backen är som brantast, men att blir
lättare att putta ju närmare kullens krön man kommer. Så även om kraften
(med mekaniska kraften alltså) minskar när man närmar sig kullens topp så
fortsätter man ändå att ge bilen mera och mera lägesenergi ju närmare
toppen den hamnar. Så när den är nästan på toppen så är den lättare att
putta än när det var långt kvar till toppen och backen var brantare.
Nu kanske någon tycker att det är ett flagrant slöseri på ord att säga en
massa om krafterna som råder mellan laddningar, när inte krafterna som
sådana är något man låter "flytta på något" i en kondensator, utan det
blir en mera lokal angelägenhet, men krafterna är faktiskt av betydelse
för att man skall kunna förstå energiriktningarna. När man drar i något
som svarar med en motkraft så inför man energi i systemet. När man låter
en förefintlig systemkrafts skapa rörelse så får man energi från det. Och
strömmar ÄR rörelser, en sorts rörelser - laddningsrörelser.
Och vad betyder då allt detta för kondensatorn?
Jo för att få en viss spänning att uppstå mellan de två i varandras närhet
befinnande folierna så behöver man få in en massa laddningar i kondensa-
torn "plus på ena sida och minus på den andra" kan man kanske tro¤, men
här nöjer oss med att tala om den relativa laddningen. Kondensatorns
ena pol jämfört med den andra.
Så vad gäller då? Jo det behövs fler och fler laddningar ju närmare varan-
dra de två folierna befinner sig för att det skall bli en viss spänning mellan
dem. Och ju större de är (yta mot varandra) desto fler laddningar behövs
även där. Seriekopplar man två kondensatorer så är det samma sak som
att dubbla avståndet mellan plattorna i en kondensator, och om man paral-
lellkopplar två kondensatorer så är det samma sak som att dubbla folieytan
på en kondensator. Det förstnämnda ger en halverad kapacitans (mängd
laddning so behöver fyllas på för att nå en viss spänning) medan det sist-
nämnda ger en dubblerad kapacitans.
Så en dubbelt så stor kondensator (t ex 2 farad) är det alltså dubbelt så
trögt att ändra laddningsspänningen på. Med detta menar jag att man
behöver hälla i dubbelt så mycket laddning (köra ström genom) för att få
samma spänningsförändring. Alltså dubbelt så hög ström in i den under
samma tid, eller samma ström men dubbelt så länge.
Kondensatorns induktans berättar om dess spänningströghet - alltså lite
förenklat om hur LÄNGE en ström behöver gå in i över den för att ändra
spänningen över den 1 volt. (Eller om hur stor strömmen behöver vara, en
lång tid eller en stor ström går lika bra - det handlar om produkten mellan
de tu.)
- - -
KAPITEL 4 - Enkelt filter = en frekvensberoende spänningsdelare!
Minns ni fortfarande kapitlet om spänningsdelaren? Om så, tänk er nu
att vi stället för det övre motståndet i spänningsdelaren använder en
spole eller en kondensator, vad händer då?
Ja, jag har ju lovat att inte komplicera med flera ekvationer, så det får
blir den där ohms lag igen: U = I*R (eller I = U/R eller R = U/I, alla är ju
samma ekvation, bara lite omstuvade).
Använder man den så vet man direkt att strömmen genom två motstånd
(R1 och R2) blir I = U/R = U/(R1+R2). Och man vet att spänningen över
den ena, t ex den som ligger "underst" (mot jord om det finns någon jord i
systemet) blir U = I*R, men I visst vi ju, så vi byter I mot U/(R1+R2).
De två ihopgyttrade versionerna av ohms lag är nu lagen för spännings-
delning! U = U*R/(R1+R2)
- - -
KAPITEN 4B - Spänningsdelning med reaktiva komponenter!
Den just visare ekvationen - som alltså är ohms lag i två versioner, ihop-
gyttrade, är sann inte bara för motstånd som är reella (vanliga motstånd),
utan även för "motstånd" som är reaktiva! Både kondensatorer och spolar
"gör ju motstånd" - de kan läggas i vägen för strömmen, således att man
förlorar lite spänning i processen, men deras impedans (det heter inte resi-
stans när man talar om vilket motstånd de gör mot en växelström) är reak-
tiv. Den kan lagra energi (magnetisk respektive elektrostatisk) men den
kan inte som en resistor omvandla elektrisk energi till värme.
Nu börjar jag närma mig slutet på denna ultraförenklade version av hur ett
(enkelt) delningsfilter fungerar och varför det fungerar så.
Och det som jag hade tänkt avsluta med är att FÖRST säga några ord om
hur stor impedans en kondensator eller en spole har, och eftersom jag ju
lovat att inte krångla till med några flera ekvationer så tänkte jag bara
skriva att en spole har ett spänningsfall per ström (ni minns väl att resis-
tans enligt ohms lag kunde beskrivas som U/I

, alltså "spänningsfall per
ström") som är proportionellt mot frekvensen och mot spolens värde****.
En kondensator har en impedans om är omvänt proportionell mot både
vinkelfrekvensen och mot sitt eget värde.
Och SEN tänkte jag säga en sak till - att den enkla version av spänning-
delare som jag beskrev har de två spänningarna (den över R2 och den över
R1) liksom staplade på varandra. Då blir spänningen över dem båda lika
stor som summan av R1s och R2s spänning. Detta gäller ju oavsett om
insignalen är en DC-spänning eller en växelspänning. I varje ögonblick är
spänningen över de två motståndet summan av det som ligger över vart
och ett av dem.
Så är inte längre fallet är man gör spänningsdelare med reaktiva kompo-
nenter...
För som ni kanske minns det jag skrev om att en kondensator laddas upp
och att det är ett fenomen med en viss tröghet. Och då minns ni kanske
också att jag beskrev att spänningen växer när strömmen gör in i konden-
satorn? Så - den maximala spänningen över den, får man när strömmen
har gått maximal tid - vilket är just när den slutat gå! Då har man max
spänning, eftersom man har maximal strömtid-produkt. Strömmen är alltså
noll vid max spänning. Tittar man över en längre tid och sinusström genom
komponenten så kan man även se att spänningen är noll (går från negativ
til postiv med maximal positiv derivata) när strömmen är maximal.
I spolfallet så råder motsatt förhållande. När spänning av obruten polaritet
ligger över den så ökar ju strömmen (strömmen är trög och växer med
tiden vid en fast spänning över spolen) och strömmen blir konstant (den
slutar ändras/får nollderivata) och maximal (given en sinussignal) när spän-
ningen över spolen är noll.
Som ni kan sluta er till, så är alltså spänning och ström fasförskjutna 90
grader (1/4 cykel) i förhållande till varandra i både kondensatorer och spol-
ar, men åt varsitt håll! Detta eftersom strömtröghet och spänningströghet
ju är varandras sanna motsatser (snarare än "långsam spole och snabb
kondensator").
Så när man adderar impedanserna från t ex en kondensator i serie med ett
motstånd för att man vill räkna ut strömmen genom dem, så måste man
tänka sig det två spänningarna som två som är staplade på varandra så
det bildas ett 90 (rätvinkligt) hörn dem emellan. Summan räknar man t ex
ut med pythagoras sats, för en rätvinklig triangel blir det ju och man ritar
de tre spänningarna. Total/in-spänningen blir hypotenusan.
De två ihopgyttrade versionerna av ohms lag är nu lagen för spännings-
delning med en reaktiv seriekomponent, och såhär blir det när R1 byts mot
C1 (vars reaktiva impedans kallas X1, eftersom X är impedansen för en
reaktiv komponent):
U = U*R/(X1+R2),#
Nöjer man sig med första ordningens filter, beloppet på utsignalen och har
turen att ha hittat högtalarelement som är rent resistiva (jovisst...) så är
det faktiskt inte svårare än så.
Vill man sedan ha utsignalens fas med så får man den från samma triangel.
Bara att titta på vinkeln mellan hypotenusan och den katet som är utspän-
ningen.
- - -
Och därmed tänkte jag att jag skulle nöja mig, bortsett ifrån en kortfattad
resumme:
Kondensatorer är spänningströga, så kopplar man dem i serie med ett hög-
talerelement så kommer de höga frekvenserna att passera fram till elemen-
tet - eftersom den tröga kondensatorn inte hinner laddas om när period-
tiden för tonen är kort. Då kondensatorn beter sig som en kortslutning för
höga frekvenser. Spelas (tillräckligt) låga frekvenser så kommer dock kon-
densatorn att hinna laddas om, och den stjäl då huvuddelen av spänningen
för elementet.
Spolar är strömtröga, så kopplar man dem i serie med ett högtalarelement
så kommer bara de låga frekvenserna att passera fram till elementet. Den
strömtröga spolen får ju vid låga frekvenser tillräckligt lång tid på sig att
bygga upp och bryta ned magnetfältet såsom krävs för att strömmen skall
slippa fram. Så den beter sig som en kortslutning för låga frekvenser. Om
det spelas (tillräckligt) höga frekvenser så kommer dock inte den magnet-
iska energin som krävs för att ström skall kunna passera, att byggas upp,
och den stjäl då huvuddelen av spänningen för elementet.
Vh, iö
- - - - -
*Vilket i själva verket är en effekt där man på likande sätt som gravitation
och tröghetskrafter är oskiljbara för ett objekt som är i acceleration eller i
ett gravitationsfält - inte kan skilja mellan EMK på grund av rörelse i ett
fält eller uppbyggnad/nedbrytning av fältet. Det är för övrigt ett faktum
som jag har som viktig utgångspunkt i min egen magnetfältsteori, där en
viktig utgångspunkt är att det finns en magnetisk eter - och att fältderi-
vata lika gärna kan beskrivas som en rådande etervind. jag skriver detta
väl medveten om att man i den akademiska världen förnekar en eter, men
till mitt försvar vill jag säga att mina ekvationer ger samma samma resultat
som med den klassiska fysikens modeller, men med magnetfältsmodell gör
åtskilliga fenomen väldigt mycket lättare att båda förstå och bolla med
fritt.
**För delningsfilterresonamanget kan vi bortse ifrån fallen där rörelser tillåts
uppstå och kan betrakta krafter inlåsta i systemet - alltså se alla delar
som ingår i systemet som ändligt mekaniskt styva. I verkligheten så är det
förstås inte alls sant att så kommer att vara fallet, men verkligheten är en
helt annat historia än en förenkling som denna - och just nu så är verklig-
heten med all sin komplexitet överkurs, minst sagt.
***Ja, en kondensator har en viss induktans - och en viss resistans dess-
utom. Och spolar har en viss kapacitans dessutom, och en viss resistans!
Jag brukar säga att komponenterna är orena, men det skall inte misstolkas
som att de behöver var dåliga. Orenhet i den här betydelsen betyder inte
distorderande. Bara att deras exakta beskrivning inte är riktigt så enkla
som den enkla matematiska modellen för dem säger. Och motstånd är ju
induktiva också - och kapacitiva!

¤Men mera på riktigt så behöver inte absolutladdningarna skilja sig belopps-
mässigt från varandra, någon absolut potential kan man inte etablera utan
att veta var kondensatorn befinner sig jämfört med jorden - och jorden är
ju till på köpet även den odefinierad i de allra flesta sammanhang, med av-
seende på absolut laddstatus. Bara i sammanhang där någonting har ladd-
ats upp till extrema nivåer och elekro-statisk reppellation av märkbar stor-
lek uppstår inom det laddade objektet, brukar man börja tala om absoluta
laddnivåer,
****Fast om man skall vara noga så brukar man inte räkna med frekvens
(cykel per sekund) när man skall bli lite djupare fysiskt utan då talar man
om radian per sekund, och varför lämnar jag till något annat tillfälle, men
man kan faktiskt påstå att skälet är trigonimetriskt, en radian (en en radie
lång cirkelbåge) är liksom ett mycket enklare mått än ett varv, även om
det kanske inte känns så för den som ännu inte dykt så ofta och djupt in
i fysiken.
#Och X1 har värdet 1/jwC, där w borde ha varit lilla omega, men den är
ju svår att skriva här på faktiskt. Och w i sin tur är 2*pi*f kanske ni minns
att jag berättade. Men eftersom jag hade lovat att bara ha med en ekva-
tion så fick detta bli sagt här efteråt istället.

- - -
PS. Det ovanstående är bara lite skrap på ytan, men förhoppningsvis kan
det vara en start - en lite lättare infallsvinkel för många än att börja med
att ge sig på ekvationerna som anger filtrens överföringsfunktioner.
För att kunna göra vettiga filter så behöver man dock både förstå hur alla
vektorer snurrar och gärna kunna räkna på det också utan hjälp av dator.
Men någonstans måste man ju starta. Hoppas det ovanstående "pladdret"
kan vara en öppning för någon att liksom börja "lära känna" de komponenter
som man använder för att skapa passiva delningsfilter. Bli vän med dem och
liksom förstå hur de är uppbyggda, och från det inse vad de gör och varför
de gör så.
Någon skrev att man kan "börja med passiva filter och sedan gå vidare till
de mera avancerade aktiva filtren", eller något liknande.
Jag tror ingen som satt sig in i de passiva filtrens värld ser det så. Utan
snarare inser man då att praktiska passiva filter faktiskt är oerhört mycket
mera komplexa än aktiva filter.
De senare kan ju kontempleras helt utan hänsyn till laster och olinjäriteter.
Det kan man förstås göra även för passiva filter, men då blir det bara pann-
kaka av alltsammans.

Fd psykoakustikforskare & ordf LTS. Nu akustiker m specialiteten
studiokontrollrum, hemmabiosar & musiklyssnrum. Även Ch. R&D
åt Carlsson och Guru, konsult åt andra + hobbyhögtalartillv (Ino).

