Svante skrev:IngOehman skrev:Svante skrev:IngOehman skrev:Och nej - det väldefinierade (max)värdet som är Gibbs fenomen, gäller INTE i CD-spelarfallet, där överslängen kan bli större än så.
Men det är intressant att du säger att överslängen kan bli större med någon annan signal än en fullt utstyrd fyrkantsvåg. Vilken signal är det?
Maxvärdet för översvängen nås med fyrkantvåg. Och de uppgår till ett högre
värden än det vi ser när vi studerar Gibbs fenomen*.
Vh, iö
- - - - -
*Istället för att studera Gibbs fenomen genom att räkna på limes oändligt
antal övertoner, så kan man studera stegsvaret för ett enskildt steg, upp-
byggt med valfri samplingsfrekvens men med SinX/X som rekonstriktions-
pulssvar (ogillar att många vill kalla detta för ett filter. Det är det inte).
Dock måste SinX/X represeteras av ett oändligt antal termer för att man
skall få en exakt siffra för överslängens storlek om inte, så på så vis är väl
kanske inte vinsten så stor med avseende på beräkningens komplexitet.
Dock är det, för de flesta nog mycket lättare att intuitivt förstå varför det
blir som det blir om man räknar på ett enskildt steg på det viset.
Allt blir ju liksom helt självklart då.
Man kan säga att man på så vis räknar på en oändligt låg frekvens istället
för att räkna med ett oändligt antal övertoner. Men kvoten är i båda fall
oändligheten, så resultatet blir lika.

Ok, nu blev jag förkryllad. Du säger att maxvärdet nås med fyrkantvåg, gärna en sådan med låg frekvens, tex så låg att den bara blir ett enda steg.
Nej det skrev jag inte.
Jag skrev på ett ställe om att överslängen (som inte har med Gibbs fenomen
attgöra) blir större än Gibbs fenomens översläng.
Och sen skrev jag även ett PS som redogjorde för ett alternativs sätt att be-
räkna eller betrakta Gibbs fenomen.
Du verkar blanda ihop dessa texter med varandra.
Men om det fått dig att tänka (och inse att överslängen av en LP-funktion
kan bli större än Gibbs fenomen, så utmärkt! Du skrev ju tidigare att Gibbs
fenomen anger maxvärdet, vilket alltså är fel.
Svante skrev:Så kan det väl inte vara, tänkte jag. Att lågpassa en fyrkantvåg måste ju vara samma sak som att bygga upp en fyrkantvåg med ett ändligt antal sinusar, och de borde därmed få lika stor ringning. Men jag missade en sak.
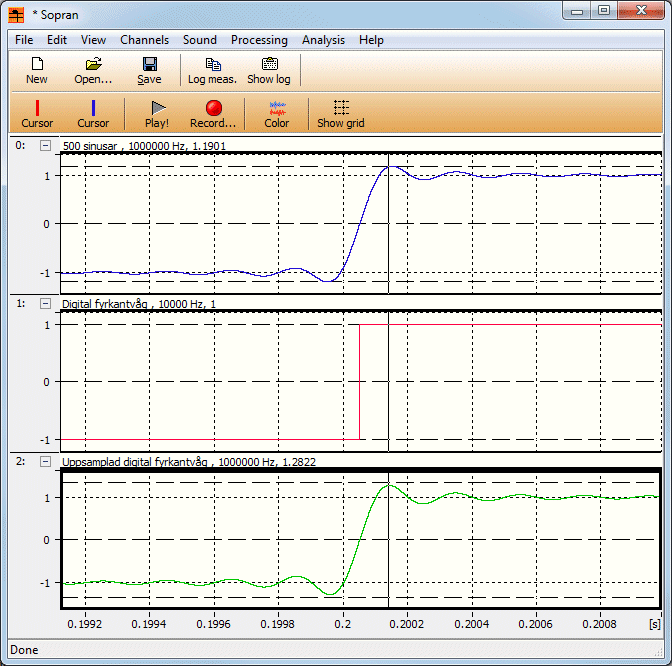
Jag syntetiserade just en 10 Hz "fyrkantvåg" med 500 deltoner och samplingsfrekvensen 100000 Hz. Jag ställde in nivån på sinusarna så att amplituden på fyrkantvågen blev +/- 1 i de plana partierna. Toppvärdet blev då 1,19. Språnget som signalen tar är 2 stort, så här har vi en overshoot på 9,5%. Lite mer än Gibbs konstant, men nära nog.
Sen vände jag på det hela i stället och gjorde en signal samplad med 10000 Hz och laddade den med en digital fyrkantvåg. Sen samplade jag upp den med superduperinställningar på min omsamplare och då fick jag ett största värde på 1,28. Hmm, vad i helvitte.
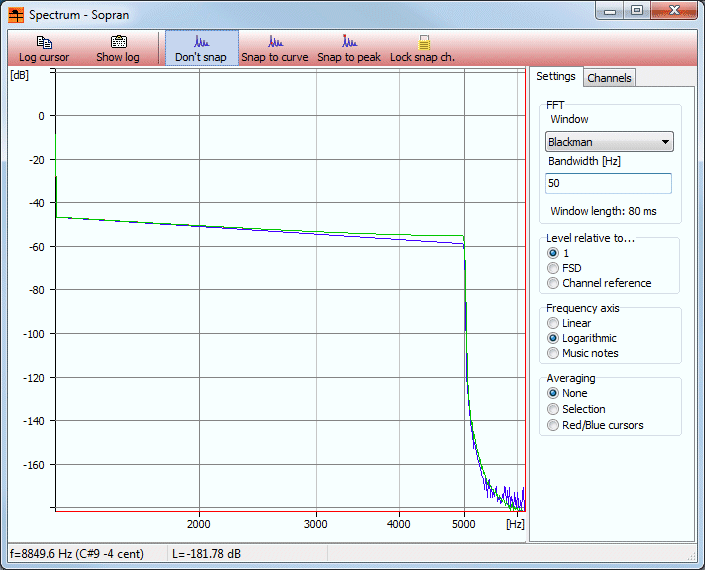
En spektralanalys ger dock förklaringen. Den digitala fyrkantvågens spektrum faller inte med 6 dB/oktav som jag hade väntat mig. Den är i stället drabbad av "vikningsdistorsion" som gör att de högre deltonerna är lite för starka. Det gör att ringningen, som ju "består av frekvenser nära brytfrekvensen" får mer energi, ringningen blir kraftigare.
Intressant. Det verkar alltså som att marginalen man behöver är ungefär 1,28 ggr fyrkantvågens toppvärde, och inte 1,19 ggr toppvärdet som Gibbs fenomen ger.
Igen - Gibbs fenomen ger inget svar på frågan överhuvudtaget. Det är bara
en upptäckt av att en oändlig serie av övertoner skapar en fyrkantvåg med
under och översläng - trots att en sprktralanalys av en ideal fyrkantvåg visar
att den innehåller just dessa spektralkomponenter. Det kan anses vara något
kontraintuitivt, och därför har det fått ett namn - Gibbs fenomen.
Men det är riktigt att marginalen kan behöva vara något annat än 1,19 ggr
toppvärdet. Vilken marginal man behöver beror på vilken rekonstruktion man
valt. Även om man avstår ifrån dumheter som att använda en rekonstruktions-
puls med spektralt innehåll över halva samplingsfrekvensen, så finns det gott
om möjligheter att inom dessa förutsättningar välja olika lösningar som i sig
renderar olika översläng.
I synnerhet när det gäller system med samplingsfrekvenser avsevärt mycket
högre än 40 kHz är jag advokat för att välja en annan och bättre rekonstruk-
tionspuls än sinX/X.
(Inte för att det betyder något får vår hörsel, men för att det kan skapa lite
bättre förutsättningar för apparaterna senare i kedjan.)
Vh, iö
Fd psykoakustikforskare & ordf LTS. Nu akustiker m specialiteten
studiokontrollrum, hemmabiosar & musiklyssnrum. Även Ch. R&D
åt Carlsson och Guru, konsult åt andra + hobbyhögtalartillv (Ino).