Mvh
Peter
Moderator: Redaktörer
Svante skrev:AndreasArvidsson skrev:Typ
Jodå jag vet. Jag bara läste Ingvars inlägg lite fort och hittade mer och mer i det när jag läste om det.
Svante skrev:RogerJoensson skrev:Precis. Bara att hoppas att volymkontrollen inte gör något skumt, men det ska väl mycket till för att misslyckas med detta.
Hur är det med förstärkare? Låter dom vanligen de inbyggda D/A gå på fullt, med volymen i analogdelen eller har man tänkt till där? Det billigaste idag borde i och för sig vara att reglera volymen digitalt före D/A, men då riskerar ju brusgolvet bli hörbart så jag gissar att man inte gör enbart så.
Så länge man har analoga ingångar så har man nog en analog volymkontroll. Ofta är den nog digitalt styrd, men ändå analog.
IngOehman skrev:Svante skrev:AndreasArvidsson skrev:Typ
Jodå jag vet. Jag bara läste Ingvars inlägg lite fort och hittade mer och mer i det när jag läste om det.
Inget problem alls. Tack för svaren.
Är dock fortfarande inte på det klara riktigt med vad det är du testar.
Att det kan bli problem i den apparat som man spelar upp musiken i är ju en sak, och visst kan
tillverkarna ta till lite för dålig marginal därvidlag således att sinc-vindlingarna/vågningen som
uppstår då man översamplar kan rendera klippning. men då är ju ändå de signaler som finns på
fonogrammet icke-nyquist-fientliga. Men det kanske de som du talar om uppfyller också.
Jag är inte säker på att jag helt förstod ditt svar med avseende på just detta.
Är i själva verket inte ens säker på att jag förstår om en signal i den digitala domänen KAN vara
nyquist-fientlig. Fast jag själv resonerade om det.
Hmm... Kan ett antal samples i den lagrade koden vara "omöjlig" i betydelsen att det inte finns
någon analog insignal som kan resultera i den, utan att innehålla energi över Fs/2?
- - -
Jag tycker att jag borde veta svaret på frågan intuitivt, men det är inte så lätt efter all påskmust
som de andra druckit, så jag slapp och fick vin istället. Att fundera går bra, men att komma fram
till något är inte lika lätt.
Får en sorts dejavu (eller hur det stavas) och associerar när jag ser dina fasvingliga fyrkantvågor
till strömförbrukningen som kan uppstå dynamiskt när man har en högtalare med reaktiv impedans.
Det är även där lätt att visa att man kan få toppströmmar mycket större än Uinmax/Zmin, men det
är också svårt att beräkna den teoretiska gränsen för hur stora toppströmmar som kan uppstå med
en insignal som är helt formfri och bara begränsad med avseende på max spänning åt både plus-
och minushållet.
Har en känsla av att det finns släktskap matematiskt, även om det är olika funktioner som "kopplar
samman" orsakande och resulterande signal, nämligen sinX/X respektive högtalarens impedans.
Vh, iö
RogerJoensson skrev:Svante skrev:RogerJoensson skrev:Precis. Bara att hoppas att volymkontrollen inte gör något skumt, men det ska väl mycket till för att misslyckas med detta.
Hur är det med förstärkare? Låter dom vanligen de inbyggda D/A gå på fullt, med volymen i analogdelen eller har man tänkt till där? Det billigaste idag borde i och för sig vara att reglera volymen digitalt före D/A, men då riskerar ju brusgolvet bli hörbart så jag gissar att man inte gör enbart så.
Så länge man har analoga ingångar så har man nog en analog volymkontroll. Ofta är den nog digitalt styrd, men ändå analog.
Jo, naturligtvis, men om man använder de digitala ingångarna... -Det var den egentliga frågan.
Benchmark DAC2 har det. Den har även 3,5dB headroom för digital klippning.Svante skrev:...så tror jag att volymkontrollen är analog om förstärkaren har analoga ingångar. Alltså jag tror inte att man har två olika volymkontroller i en förstärkare.
"HGC" is Benchmark's unique Hybrid Gain Control system. The DAC2 HGC combines active analog gain control, passive low-impedance attenuators, a 32-bit digital gain control, and a servo-driven volume control. All inputs are controlled by the rotary volume control. This volume control moves in response to commands from the remote control. Analog inputs are never converted to digital, and digital inputs never pass through an analog potentiometer.
Alexi skrev:Benchmark DAC2 har det.Svante skrev:...så tror jag att volymkontrollen är analog om förstärkaren har analoga ingångar. Alltså jag tror inte att man har två olika volymkontroller i en förstärkare.
Piotr skrev:Antar att det är knepigt att ta höjd för alla tänkbara rekonstruktionsfilter.
Svante skrev:IngOehman skrev:Inget problem alls. Tack för svaren.Svante skrev:Jodå jag vet. Jag bara läste Ingvars inlägg lite fort och hittade mer och mer i det när jag läste om det.
Är dock fortfarande inte på det klara riktigt med vad det är du testar.
Att det kan bli problem i den apparat som man spelar upp musiken i är ju en sak, och visst kan
tillverkarna ta till lite för dålig marginal därvidlag således att sinc-vindlingarna/vågningen som
uppstår då man översamplar kan rendera klippning. men då är ju ändå de signaler som finns på
fonogrammet icke-nyquist-fientliga. Men det kanske de som du talar om uppfyller också.
Jag är inte säker på att jag helt förstod ditt svar med avseende på just detta.
Är i själva verket inte ens säker på att jag förstår om en signal i den digitala domänen KAN vara
nyquist-fientlig. Fast jag själv resonerade om det.
Hmm... Kan ett antal samples i den lagrade koden vara "omöjlig" i betydelsen att det inte finns
någon analog insignal som kan resultera i den, utan att innehålla energi över Fs/2?
- - -
Jag tycker att jag borde veta svaret på frågan intuitivt, men det är inte så lätt efter all påskmust
som de andra druckit, så jag slapp och fick vin istället. Att fundera går bra, men att komma fram
till något är inte lika lätt.
Får en sorts dejavu (eller hur det stavas) och associerar när jag ser dina fasvingliga fyrkantvågor
till strömförbrukningen som kan uppstå dynamiskt när man har en högtalare med reaktiv impedans.
Det är även där lätt att visa att man kan få toppströmmar mycket större än Uinmax/Zmin, men det
är också svårt att beräkna den teoretiska gränsen för hur stora toppströmmar som kan uppstå med
en insignal som är helt formfri och bara begränsad med avseende på max spänning åt både plus-
och minushållet.
Har en känsla av att det finns släktskap matematiskt, även om det är olika funktioner som "kopplar
samman" orsakande och resulterande signal, nämligen sinX/X respektive högtalarens impedans.
Vh, iö
Hmm, nuskavise om jag kan uttrycka mig bättre.
Alltså jag försöker hitta en digital signal som är sådan att den efter uppsampling ger så högt toppvärde som möjligt. Som du säger kan inte en digital signal vara nyqvistvidrig, signalen innehåller ju per (den vanligaste) definition(en) endast frekvenser under fs/2. Jag tänkte mig närmast att om man klipper en signal i den digitala domänen så bildas det övertoner, men eftersom de inte kan ligga över fs/2 så viks de ner under fs/2.
Så signalen jag har är alltså helt syntetisk, det finns nog en analog signal som man skulle kunna sampla så att den blir som min digitala signal, men det har jag inte brytt mig om.
Svante skrev:Jag känner mig i stället väldigt artistisk och fri och skapar signalen som jag vill i den digitala domänen.
Svante skrev:I varje fall kan signalen rekonstrueras till en analog bandbegränsad signal, möjligen med reservationen att amplutuden måste vara oändlig i en punkt. Hmm...
Svante skrev:...men den digitala signalen är alltså begränsad till +/-1 (=full utstyrning) och efter omsampling blev den mer än 10 dB starkare och jag tror mig ha visat att den kan bli hur stor som helst, givet ett idealt rekonstruktionsfilter.
Svante skrev:Dessutom tar jag mig friheten att leka med rekonstruktionsfiltret, jag har ju skrivit uppsamplaren själv så då går ju det. Det visade sig att den vanliga inställningen, där jag inte har en riktig sinc, utan en som dämpas lite mer i svansarna, och som svänger lite långsammare än sincen ger mindre översläng än den nära ideala* långa trunkerade sincen med 20000 perioder.
IngOehman skrev:Svante skrev:I varje fall kan signalen rekonstrueras till en analog bandbegränsad signal, möjligen med reservationen att amplutuden måste vara oändlig i en punkt. Hmm...
Min känsla är att amplituden inte kan bli oändlig, eftersom sincens vindlingars sammanlagda amplitudtid-
produkt inte går mot oändligheten ens om man integrerar från minus oändligheten till plus oändligheten.
Men jag är inte säker.Svante skrev:...men den digitala signalen är alltså begränsad till +/-1 (=full utstyrning) och efter omsampling blev den mer än 10 dB starkare och jag tror mig ha visat att den kan bli hur stor som helst, givet ett idealt rekonstruktionsfilter.
Det beviset tror jag att jag har missat. Har du lust att repetera eller förtydliga dig? Jag har ju sett att du
genom att fortsätta leta har lyckats hitta högre och högre toppar, men det säger ju inte att limes per de-
finition blir oändligheten, det kan ju lika gärna vara ett ändligt tal, eller?
IngOehman skrev:Jag hinner inte räkna just nu, men jag tycker det ser ut som om du räknar fel. Fast jag kan ha
fel. Måste springa. Återkommer.
Men kontrollfråga: Är du med på att du, om ditt påstående är riktigt, även måste kunna rita en
analog vågform utan spektrala komponenter över halva samplingsfrekvensen, som har en oändlig
peak-amplitud, men som ändå kan samplas med ytterst små samplingsvärden...
IngOehman skrev:Eller kan det vara så att problemet är att du satt luckan till noll? Alltså att du utgår ifrån att man
samplingsteoremet säger att insignalen får innehålla frekvensen Fs/2, snarare än att den inte får
göra det, alltså att hägsta frekvensen som innehålls måste vara <Fs. Att ADCns ingång måste vara
fri från frekvensen ifråga (eftersom den ger spegling till DC)?
Vh, iö
lilltroll skrev:Tror jag kan bräcka det där lite lite till, efter att ha räknat lite komplex-analys kombinerat med vektor-analys med penna och papper.
Jag tror att om din sinc går från sample -m:m, så blir den värsta tänkbara amplituden
summan av n [-m m] av funktionen abs(1/(pi(n-0.5)))
Ett exempel:
>> n=-10000:10000;
>> sum(abs(1./(pi*(n-0.5))))
ans = 7.1135
Den där summan kan omskrivas som en konstant + summan av n [1 m] av 2/(pi*(n-0.5)), och den sista summan har en analytisk lösning vill jag minnas http://en.wikipedia.org/wiki/Harmonic_number
Men innan vi tar den är ju frågan om mitt resultat är rätt
Någon till som vågar sig på ett analytiskt svar här?
Mitt numeriska svar ovan verkar inte helt tokigt jämfört med Svantes helt numeriska test tidigare.
The associated harmonic series grows without limit, albeit very slowly, roughly approaching the natural logarithm function.
Svante skrev:IngOehman skrev:Jag hinner inte räkna just nu, men jag tycker det ser ut som om du räknar fel. Fast jag kan ha
fel. Måste springa. Återkommer.
Men kontrollfråga: Är du med på att du, om ditt påstående är riktigt, även måste kunna rita en
analog vågform utan spektrala komponenter över halva samplingsfrekvensen, som har en oändlig
peak-amplitud, men som ändå kan samplas med ytterst små samplingsvärden...
Ja, det är lite överraskande, men blir det ja. Tror jag.
Är du med på att sum ( 1 +1/3 + 1/5 + 1/7 ...) = inf ?
Svante skrev:IngOehman skrev:Eller kan det vara så att problemet är att du satt luckan till noll? Alltså att du utgår ifrån att man
samplingsteoremet säger att insignalen får innehålla frekvensen Fs/2, snarare än att den inte får
göra det, alltså att hägsta frekvensen som innehålls måste vara <Fs. Att ADCns ingång måste vara
fri från frekvensen ifråga (eftersom den ger spegling till DC)?
Vh, iö
Luckan?
Svante skrev:Jag tänker gärna på sånt här i termer av DFT och går i limes.
När man gör tex en 256-punkters DFT så matar man in 256 komplexa tal och får ut 256 komplexa tal. Enklast blir det om man låter imaginärdelen i indata vara noll, då blir informationen över fs/2 speglad. 1:a och 128:e samplet i utdata motsvarar då hur mycket DC det finns och hur mycket av fs/2 det finns. De innehåller dock ingen info om fasläget på de två. Inget av dem är meningsfullt, man kan visserligen se DC som en sinus som har fastnat med frekvensen noll och fasläget 90 grader, eller något annat fasläge.
Svante skrev:Siffran som kommer ut DFTn motsvarar 90 grader (eller att det är en cosinus och 0 grader). På samma sätt motsvarar siffran i fs/2 amplituden av fs/2 med fasläge 0 (eller om det är 90 grader, jag minns inte vilket).
Så samplingsteoremet innefattar även ett frekvensinnehåll VID fs/2, men utan fasinformation.
När man har tänkt så en stund kan man gå i limes och se att samma sak gäller även då.
IngOehman skrev:Svante skrev:Jag tänker gärna på sånt här i termer av DFT och går i limes.
När man gör tex en 256-punkters DFT så matar man in 256 komplexa tal och får ut 256 komplexa tal. Enklast blir det om man låter imaginärdelen i indata vara noll, då blir informationen över fs/2 speglad. 1:a och 128:e samplet i utdata motsvarar då hur mycket DC det finns och hur mycket av fs/2 det finns. De innehåller dock ingen info om fasläget på de två. Inget av dem är meningsfullt, man kan visserligen se DC som en sinus som har fastnat med frekvensen noll och fasläget 90 grader, eller något annat fasläge.
Ja, och min poäng är att denna DC-signal inte är en ursprungsignal. Det tillåts inte av samplings-
teoremet. Den ursprungliga sinustonen kan inte repreduceras ens med oändligt många termer i
rekonstruktionsfiltret. Därför är den otillåten.
Svante skrev:>> f=fft(p)
f =
Columns 1 through 4
0.0000 + 0.0000i 2.0000 - 4.8284i 0.0000 + 0.0000i 2.0000 - 0.8284i
Columns 5 through 8
0.0000 + 0.0000i 2.0000 + 0.8284i 0.0000 + 0.0000i 2.0000 + 4.8284i
Här får man frekvenskomponenter i f(2) och f(4) (och speglingar vid f(8) och f(6)), vilket motsvarar grundton och tredjeton. Dessa båda frekvenskomponenter är alldeles nödvändiga för att återskapa den ursprungliga digitala vågformen [1 1 1 1 -1 -1 -1 -1].
Svante skrev:IngOehman skrev:Svante skrev:Jag tänker gärna på sånt här i termer av DFT och går i limes.
När man gör tex en 256-punkters DFT så matar man in 256 komplexa tal och får ut 256 komplexa tal. Enklast blir det om man låter imaginärdelen i indata vara noll, då blir informationen över fs/2 speglad. 1:a och 128:e samplet i utdata motsvarar då hur mycket DC det finns och hur mycket av fs/2 det finns. De innehåller dock ingen info om fasläget på de två. Inget av dem är meningsfullt, man kan visserligen se DC som en sinus som har fastnat med frekvensen noll och fasläget 90 grader, eller något annat fasläge.
Ja, och min poäng är att denna DC-signal inte är en ursprungsignal. Det tillåts inte av samplings-
teoremet. Den ursprungliga sinustonen kan inte repreduceras ens med oändligt många termer i
rekonstruktionsfiltret. Därför är den otillåten.
DC-signalen är i allra högsta grad tillåten. Men den har ingenting med signalen vid fs/2 att göra, annat än att de båda beskrivs utan fasläge. Tittar man på vad som händer i fouriertransformen är DC-komponenten helt enkelt medelvärdet av alla sampel. Eller möjligen summan, beroende på vilken variant av FT man använder.
IngOehman skrev:Och vad du menar med att man får någon meningsfull information (amplitud men inte fas) om frek-
vensen F = Fs/2 förstår jag inte. Det får man ju inte. Om samplen hamnar i nollgenomgången så
blir ju sampelvärdena noll. Om nollgenomgångarna inte sammanfaller med samplingsögonblicken
så får man förvisso kodad signal, men kan inte veta hur stor den är i förhållande till insignalens
verkliga amplitud.
Kort sagt - Fin < Fs/2 är ett krav.
IngOehman skrev:Jag kan t ex tycka att sincens brickwallfrekvens skall ligga så många Hz under Fs/2 att periodtiden
för frekvensskillnaden är liten i förhållande till den tid som använd "sinc" är representerad.
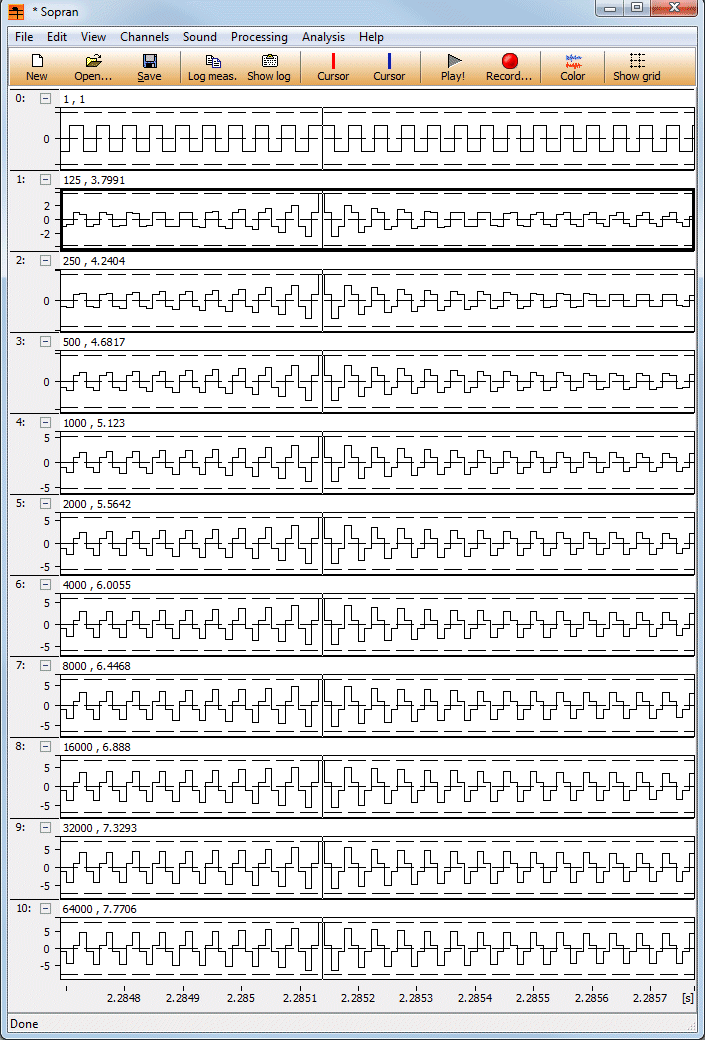
IngOehman skrev:Det betyder ju inte att du inte kan få ha din Fs/2-digitala signal, bara att den i en vettig DAC (med
sitt lika vettiga översamplingsfilter) inte kommer att kunna ställa till det.
Användare som besöker denna kategori: Inga registrerade användare och 8 gäster