Jag kan börja med att tala om svaret redan nu: Om signalen är svag, eller om frekvenserna i signalen korrelerar med samplingsklockan får man kvantiseringsdistorsion, annars blir det kvantiseringsbrus. Lägger man till ditherbrus så blir det bara kvantiseringsbrus och signalberoendet/kvantiseringsdistorsionen är borta.
--------------------------------
Så:
Om vi börjar med det som är lätt att förstå. Om vi tex tar en sinus med frekvensen fs/11 (elva) och samplar den med alldeles för låg upplösning, tex 4 bitar, så kommer signalen att få ett spektrum som i den här figuren:
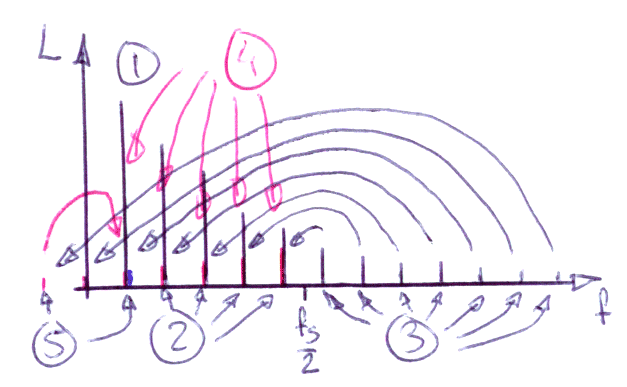
Signalen vi är intresserade av hamnar vid (1) och sedan bildas det övertoner vid (2) och (3). Övertonerna vid (3) viks ner under fs/2 som de röda pinnarna (4). En del av dem ligger över fs (endast en utritad här) och de hamnar under 0 Hz, vilket gör att de viks ytterligare en gång (5). Eftersom signalens frekvens förhåller sig till samplingsfrekvensen som ett heltal (11) så sammanfaller de vikta deltonerna med distorsionskomponenterna under fs/2.
Vi kommer att se effekterna av amplitudkvantiseringen som kvantiseringsdistorsion eftersom det blir diskreta deltoner som i detta fall dessutom är jämna multiplar av grundtonen.
Som det brukar vara med distorsion, så blir de lägre distorsionskomponenterna (2:a- och 3:e-tonsdistorsionen) starkare än de högre.
-------------------------
Om vi ökar upplösningen i samplingen (tex från 4 till 16 bitar) så kommer distorsionskomponenterna att bli svagare, men det händer dessutom något med spektrum på distorsionen. Distorsionskomponenterna får närapå samma amplitud, dvs en större andel av distorsionen förskjuts mot höga frekvenser.
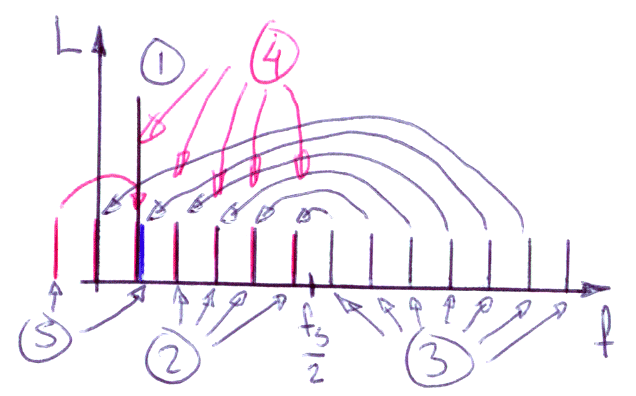
I detta fall spelar det "vitare" distorsionsspektrumet ingen större roll eftersom även dessa distorsionskomponenter kommer att sammanfalla med distorsionskomponeterna under fs/2 (pga heltalsfaktorn 11).
Vi kommer fortfarande att se effekterna av kvantiseringen som kvantiseringsdistorsion, givet att faktorn är exakt ett heltal (tex 11).
-------------------------
Om vi nu i stället tar en signal som inte är synkroniserad med samplingsfrekvensen, utan kanske ligger på fs/11,4 och kvantiserar den med dålig upplösning så blir det så här:
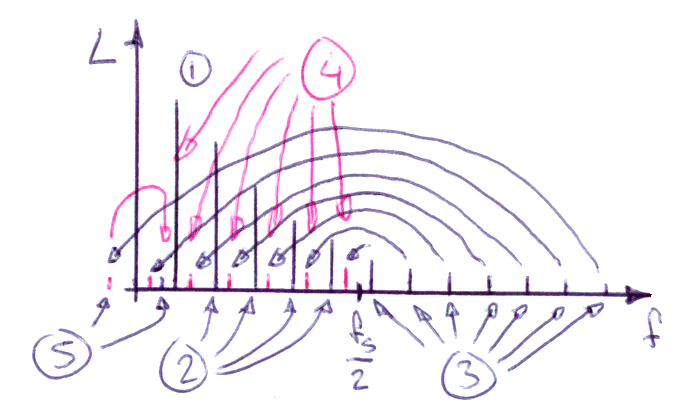
Det bildas som tidigare distorsion, men vikningen av dem kommer att ske till frekvenser mellan distorsionskomponeterna under fs/2. Det blir nu inte som tidigare "ren" harmonisk distorsion, utan en sörja av inharmoniska deltoner. Dock kommer de lägre ordningens komponenter (2:a- och 3-ton) att vara starkast, och de kommer att sticka upp över de övriga och fortsatt vara signalberoende.
Det blir alltså även här distorsion.
-------------------------
Till sist, om signalen kvantiseras med många bitar (tex 16) så kommer spektrum på distorsionen att bli alltmer "vitt", dvs deltonerna får närapå samma amplitud. När de därefter viks ner under fs/2 så blir de så många (även deltoner högt upp över fs är ju tillräckligt starka för att synas efter multipla vikningar) att de tillsammans bildar en brusliknande signal. Och så länge som signalen är stark relativt kvantiseringssteget kommer den att vara ungefär densamma; ett vitt brus.
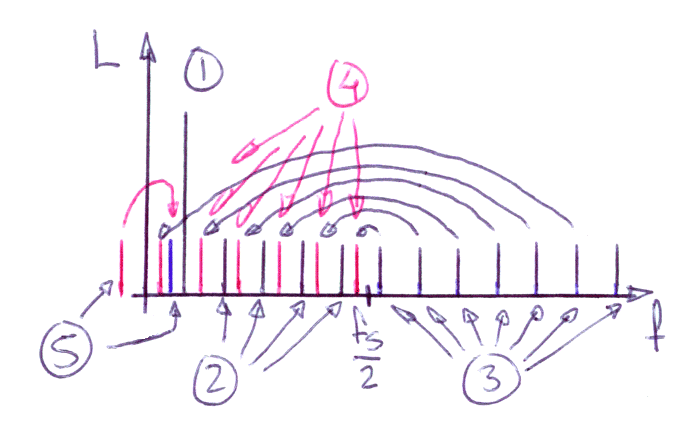
I figuren har jag inte ritat ut tillräckligt många deltoner för att man ska se att det blir ett vitt brus, dock.
-------------------------
Det är alltså bara i fallet när man har ett icke-heltalsförhållande mellan signalfrekvens och samplingsfrekvens och dessutom en stor upplösning som sampling av en enda ton är någorlunda problemfri. Kvantiseringsfelet kommer att bli signalberoende. I de tre första fallen blev det ju kvantiseringsdistorsion och inte kvantiseringsbrus. Det första kravet med osynkad signal och samplingsfrekvens är inte så svårt när det gäller musik (men väl i tankemodeller), det andra däremot är svårt. Man vill ju kunna spela in även svaga ljud.
Lösningen på problemet är enkel. Man lägger till en brussignal som är ungefär lika stark som kvantiseringssteget innan man utför amplitudkvantiseringen. Detta brus kallas för ditherbrus, efter engelskans dither=vackla, tveka. Då blir kvantiseringsfelet inte övertoner till nyttosignalen, utan brus. I stället för pinnarna vid (2) och (3) blir det en matta av brus redan innan vikningen. Om man gör det så är alla problem med distorsion helt borta och kvantiseringsdistorsionen ett minne blott
