Hur ser egentligen en analog ljudsignal ut?

[Loud]

Jag har förstått det som att en analog ljud signal är en mix av en massa sinusvågar av en olika amplituder och frekvenser. Men hur fungerar detta? Kan det gå flera olika signaler i en och samma ledning?
Och isåfall så borde ju högtalaren bara "se" den signal som har störst amplitud och spela den isåfall? Hur "vet" elementet vilken av dessa signaler den ska spela?

Eller är ljudsignalen EN ENDA lång våg som varierar i frekvens och amplitud? Så får respektive element sin beskärda del av denna våg? (det borde ju göra att elementen inte får signal hela tiden).

Läst runt och frågat en massa men är fortfarande sjukt förvirrad

[Almen]

Det är faktiskt en jättebra fråga! Den bör man fundera på så att man får en bra bild av hur det funkar.

Börja med att inte fokusera på att det är en massa olika frekvenser, utan se det som en kontinurligt varierande signal. Börja i orkestern som spelar - visserligen är det en massa instrument med en massa olika frekvenser (både grundtoner och övertoner), men det når dina öron som en komplett ljudvåg.

Denna ljudvåg omvandlas till en endimensionell elektrisk signal i mikrofonen, lagras eventuellt för att sedan förstärkas och skickas ut till högtalarna, fortfarande som en enda kontinuerlig signal. I högtalarna delas signalen upp i oika frekvensband i filtret, beroende på om det är en tvåvägs, trevägs (eller något annat).

Ut ut högtalaren kommer sedan förhoppningsvis något som liknar den ursprungliga ljudvågen.

Sedan kan man, när man analyserar vad som händer, med fördel dela upp signalen i alla sina frekvenskomponenter, men det är mest för att det är enklare att hantera rent matematiskt.

Viktigt är att skilja på om du tittar på signalen i frekvensplanet eller i amplitudplanet. I frekvensplanet tittar du på de enskilda frekvenskomponenterna, i tidsplanet på den kontinuerligt varierande signalen.

Det var mina amatörsynpunkter.

[celef]

bäst är egna experiment

ett oscilloskåp är jättebra, kan nog laddas ned från internet gratis nånstans ifrån

mata in signalen och titta på vågformen


men börja med en frekvens
öka till två
sedan tre
fyra
fem
sen kan man titta på brus

[Slartibartfast]

Ett hårt anslag som klingar ut i den övre. Du ser att själva utklingningen också är vågformad? Där har vi alltså två frekvenser (den ena med frekvenen 1/(2:59.1-2:59.0)=10Hz och sedan har vi bärfrekvensen (den som är den stora mängde sick-sack som kanske har frekvensen 1/(2:59.1-2:59.09)=100Hz - väldigt höftat) som sitter ihop och bilder ett tonspektra för det ljudet. Finns säkert fler frekvenskomponenter, men för att visa vad jag menar behövs bara två.


Så här ser en amplitudmodulerad signal ut, som en ljudsignal kan se ut alltså. Så här funkar också AM bandet på en radio - AmplitudModulerad liksom.

För att sedan alla de här jättemånga olika tonerna ska komma till rätt högtalarelement i högtalaren så använder man sig av ett delningsfilter. Ett delningsfilter är igentligen bara en form av strömdelning/spänningsdelning i enlighet med den grundläggande elläran - en spole får ökad resistans för korta våglängder (höga frekvenser) och en kondensator får ökad resistans för långa (låga frekvenser) våglängder, om man ska se det lite förenklat - och det som bestämmer brytfrekvensen för filtret är då kapacitansen i kondensatorn (hur stor laddning den kan bära givet en given potential - spänning - över sig) och induktansen (fältstyrkan givet en strömstyrka) i spolen. Alltså kommer det bli högt motstånd för frekvenser att gå fel väg, och precis som många människor väljder de frekvenserna den lättare vägen.

Signalen som kommer in till högtalaren är tidskontinuerlig men kan ha amplituden noll - alltså inte ge något utslag alls - och högtalarelementen i sig gör bara sitt bästa för att exakt kopiera den tidskontinuerliga insignalen. Ett dåligt element gör det dåligt - kan man väl säga rent krasst.

Var några år sedan jag lekte i elläran så om jag har fel på benämningar så korrigera gärna. Tror inte jag har några direkta sakfel iaf, inte vad jag kunde se just nu. Hoppas det blev lite klarare iaf!

[slrt]

[Svante]

En vinkling till då:

En analog signal kan se ut hur som helst, tex som de slarti visade. Alltså egentligen ser den ju inte ut, men man brukar rita den så, hur tex en spänning eller lufttrycket varierar som funktion av tiden. Det kallas för funktion, det där när det för varje tidpunkt bara finns ett enda värde.

Det räcker egentligen så. Grafen som visar hur signalen varierar som funktion av tiden innehåller allt som finns i ljudet. Men man kan vrida och vända på det och se den ur andra synvinklar.

Örat inför en del signalprocessning som gör att vågformen inte korrelerar sådär omedelbart med vågformen. Visst, all information finns där, men den tolkas lite olika av ögat och örat.

Det är då man börjar prata om frekvenser. Via fouriertransform=spektralanalys kan man tänka sig att vågformen är uppbyggd av en massa sinusar. Fourier visade just det; att vilken vågform som helst kan ses som en summa av sinusar. Varje sinus har en frekvens och ett fasläge. Ritar man en graf över styrkan på de olika sinusarna, som funktion av frekvensen, så har man ritat upp spektrum för signalen. Gör man det så har man kastat bort hälften av informationen, nämligen fasinformationen, men samtidigt har man fått en graf som korrelerar mycket bättre till hörselintrycket.

Så det där med olika frekvenser är bara ett annat synsätt, det tillför i princip ingen information, men gör det lättare att tolka den information som redan finns i vågformen.

[Loud]

Tack för väldigt intressanta svar! Det här har gjort mig mycket klokare, men nu kommer jag till frågan som jag funderat massa på men inte kunna komma fram till någon slutsats.

Säg att man drar på med både baskagge och symbal samtidigt. Det här bildar ju två olika ljudvågor egentligen, med olika frekvens och amplitud. Att dessa på något sätt summeras i mikrofonen, precis som i örat förstår jag, men hur ser detta ut när ljudsignalen ritas upp som en graf? Och hur "styckas" denna signal sedan när den fördelas i högtalarelementen?

Jag har tittat på lite olika ljudvågor men inte kunnat komma fram till något.
Här mina funderingar.
http://img215.imageshack.us/img215/6875/ljudvgorxo1.jpg

Tanke 1 är att mer högfrekventa ljud lägger sig som en topp på den mer lågfrekventa vågen. Går då toppen på vågen går vidare till diskanten? Vågen kommer ju vara en DC signal och kommer därför inte få membranet i diskanten att röra sig fram och tillbaka?

Jag har sett såna här små vågor ovan på stora vågor på dom grafer jag tittat på men inte kunnat förstå om det är brum, eller om det är en relevant del av signalen? Om det är en DC signal, så borde ju teoretiskt fortfarande elementet kunna förflyttas av det, förutsatt att membranets fjäderkraft är alert. När amplituden hela tiden svänger så borde det göra att vid en topp på grafen så trycks membranet fram lite, för att sedan fjädra tillbaka lite i en dal?

Eller är det bara AC signaler som för elementen att röra sig?

Tanke 2 är att lågfrekventa och högfrekventa vågor "turas om". Då blir det ju så gott som hela tiden en AC signal, men om två ljud spelas in samtidigt borde dom ju synas samtidigt på grafen med?

Eller är det i verkligheten en kombination av allt?

Hoppas jag inte dumförklarat mig för alltid nu Har frågat flera duktiga personer om detta men har inte förstått riktigt.

[Tore]

Säg att man drar på med både baskagge och symbal samtidigt. Det här bildar ju två olika ljudvågor egentligen, med olika frekvens och amplitud. Att dessa på något sätt summeras i mikrofonen, precis som i örat förstår jag, men hur ser detta ut när ljudsignalen ritas upp som en graf? Och hur "styckas" denna signal sedan när den fördelas i högtalarelementen?

Enkelt exempel:



+



=



Sedan kan man köra signalen genom filter som separerar lågfrekvent från högfrekvent igen. Ett sådant filter sitter i högtalaren.

(Det är alltså inte så att det högfrekventa ljudet bara ligger i "topparna" eller att de "turas om" som du föreslog, utan höga och låga frekvenser ligger blandade "hela vägen".)

[SlaitH]

Tore du föregick mig.

Bra exempel!

Patrik

[Loud]

Okej

Men detta innebär att dom högfrekventa signalerna i exemplet blir DC signaler? Eftersom dom högfrekventa vågorna här aldrig korsar X-axeln, förutom mellan varje lågfrekvent våg?

[guldfisk]

Nej. Du får se den lågfrekventa vågen som den högfrekventas X-axel.

[skrutten]

Okej

Men detta innebär att dom högfrekventa signalerna i exemplet blir DC signaler? Eftersom dom högfrekventa vågorna här aldrig korsar X-axeln, förutom mellan varje lågfrekvent våg?

Vad betyder DC i detta fall?

[SlaitH]

För vetskap så är loud praktikant på mitt jobb. (Ifall följande blir lite luddigt)

Vi kan göra en labb på måndag så ska jag visa dig med oscilloskop och två tongeneratorer.

Ps. Det är nog jag som inte är så bra på att förklara när frågan har ställts.

Patrik

[Loud]

Fan va gött

Eller så är det jag som inte kan formulera frågor så folk förstår

[n3mmr]

För vetskap så är loud praktikant på mitt jobb. (Ifall följande blir lite luddigt)

Vi kan göra en labb på måndag så ska jag visa dig med oscilloskop och två tongeneratorer.

Ps. Det är nog jag som inte är så bra på att förklara när frågan har ställts.

Patrik

Glöm inte prov efteråt!

[Max_Headroom]

Okej

Men detta innebär att dom högfrekventa signalerna i exemplet blir DC signaler? Eftersom dom högfrekventa vågorna här aldrig korsar X-axeln, förutom mellan varje lågfrekvent våg?

Det här med frekvenser är inte lätt. Inte blir det lättare av att alla exempel visar hela perioder. Men frekvens kan ses som derivata, dvs hur brant kurvan går uppåt (eller nedåt). Tänk dig bara en liten del av dom kurvor som visats här i tråden. Kurvan lutar ju där också.

En bra (?) förståelse kan man också få genom att laborera med ljudsyntes (helst då någon gamal analogsynth eller motsvarande mjukvarusynt på dator). Då kan man prova olika vågformer och filtrera dom. Ett ljudprorgam på datorn som komplement är också bra, så man kan titta på vågformen där och se vad som händer.

Det tog åratal innan jag började förstå vad frekvens är och vad filter i högtalare gör, egentligen, när dom delar upp frekvenser till olika element. Det var också i den vevan jag insåg hur enormt svårt det är att få till en bra högatalare.

[Tore]

Det här med frekvenser är inte lätt. Inte blir det lättare av att alla exempel visar hela perioder. Men frekvens kan ses som derivata, dvs hur brant kurvan går uppåt (eller nedåt).

Nja, derivatan beror lika mycket på amplituden som på frekvensen och varierar dessutom med fasen. Tror nog fortfarande att det är enklast att förstå frekvens som antalet svängningar per tidsenhet.

[Piotr]

Nja, derivatan beror lika mycket på amplituden som på frekvensen och varierar dessutom med fasen. Tror nog fortfarande att det är enklast att förstå frekvens som antalet svängningar per tidsenhet.

Medhåll!


/Peter

[Max_Headroom]

Det här med frekvenser är inte lätt. Inte blir det lättare av att alla exempel visar hela perioder. Men frekvens kan ses som derivata, dvs hur brant kurvan går uppåt (eller nedåt).

Nja, derivatan beror lika mycket på amplituden som på frekvensen och varierar dessutom med fasen. Tror nog fortfarande att det är enklast att förstå frekvens som antalet svängningar per tidsenhet.

Det beror kanske på vad man har för hjärna... Min tycker det är enklare om man tittar på lutningen. Med svängningar per tidsenhet så ärdet så lätt att man fastna i tänket att man ska passera X-axeln. Och det ska man långt i från alltid om manbara ser på en liten del av vågformen.

Kanske är också synsätten olka bra beroende på vad man studerar?

[Svante]

Det här med frekvenser är inte lätt. Inte blir det lättare av att alla exempel visar hela perioder. Men frekvens kan ses som derivata, dvs hur brant kurvan går uppåt (eller nedåt).

Nja, derivatan beror lika mycket på amplituden som på frekvensen och varierar dessutom med fasen. Tror nog fortfarande att det är enklast att förstå frekvens som antalet svängningar per tidsenhet.

Frekvens betyder just "oftighet", hur många per tidsehet.

Sen blir det ju så att om man spelar upp en signal dubbelt så fort, dvs den får dubbla frekvensen, och om man samtidigt behåller amplituden, ja då blir alla lutningar dubbelt så stora. Ändå är det så att det inte går att utläsa frekvensen eller frekvensinnehållet i en signal bara genom att titta på lutningen.

Titta bara på dessa två signaler, som har samma frekvensinnehåll, men där tredje deltonen byter fasläge. Derivatan blir rätt olika.

[tvett]

Ac och Dc....... Ac är Dc med olika amplitud, hur ofta det växlar tecken åt ett håll är frekvensen

[Tore]

Det beror kanske på vad man har för hjärna... Min tycker det är enklare om man tittar på lutningen. Med svängningar per tidsenhet så ärdet så lätt att man fastna i tänket att man ska passera X-axeln. Och det ska man långt i från alltid om manbara ser på en liten del av vågformen.

Problemet, som jag nämnde, är att lutningen i sig inte säger särskilt mycket om frekvensen, och tittar man bara på en liten del av vågformen kan man inte i allmänhet avgöra vad det är för frekvens.

Hur som helst, inspirerad av Louds fråga slängde jag ihop en liten Java-applet som man kan leka med här. Förhoppningsvis kan den vara till glädje för någon.

[Zzombie]

En annan dimension på analogt ljud är Attack, Sustain, Decay, Release...
Kapar man bort Attack (anslaget) på en ton, är det mycket svårt att avgöra vilket instrument det är frågan om...

[Loud]

Jag lämnade det här ämnet några år men nu medan jag bygger en ljusorgel tog jag upp det igen och fördjupade mig lite. Det är sjukt intressant. Jag bevisade till slut lite samband för mig själv med formler och resonemanget verkar hålla. Förmodligen kan jag nu börja sova om nätterna igen.

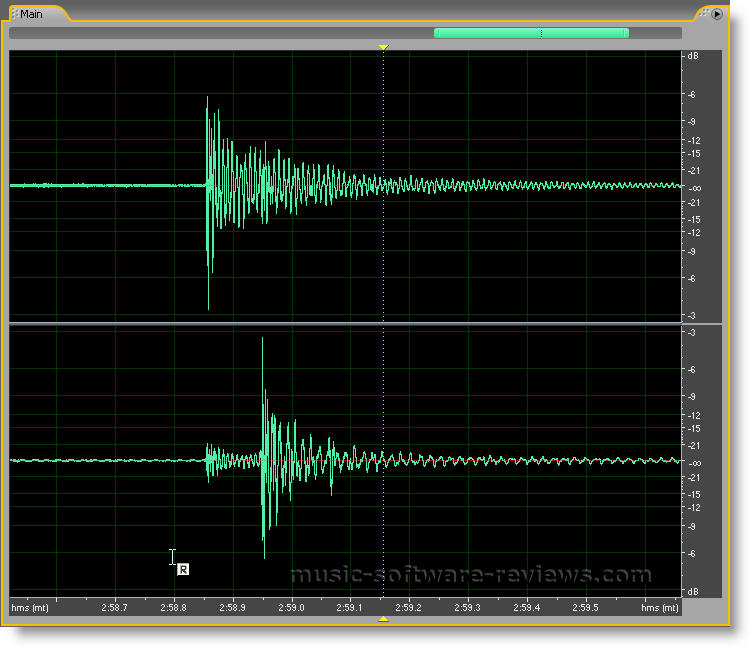
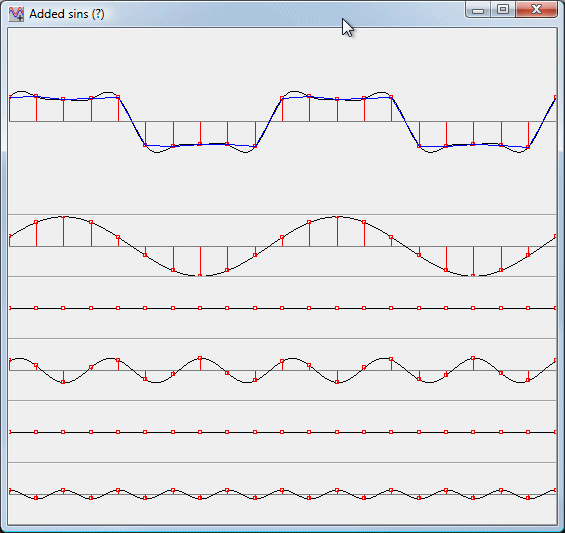
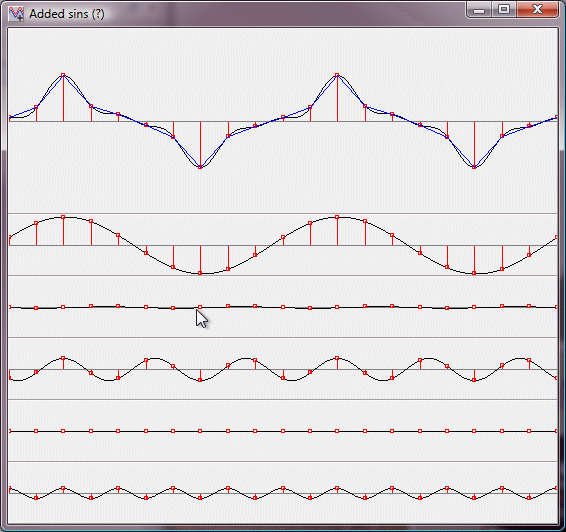
Jag har kommit fram till att det är spänningsderivatan som bestämmer strömmen genom en kondensator. Derivatan är ju en funktion både av frekvensen och amplituden som man enkelt kan se genom att titta på grafer i praktiken med t.ex. denna excellenta applikation:

http://web.comhem.se/~u38201378/sine/SineApp.html

Till beviset!

Definitioner:

C = kapacitans
Q = laddning
U = spänning
I = ström
t = tid
d = prefixet delta, (visar på differens)



Kapacitans är antalet laddningar som ryms i kondensatorn per volt den laddas med.

Kapacitans C=Q/U


Ström definieras som antalet laddningar som passerar i en ledare på en viss tid

Ström: I = Q/t , eller I = d(Q)/d(t) .

Derivatan av spänningen är hur fort spänningen ökar över kondensatorn

Spänningsderivata: U/t, eller d(U) / d(t)

Antalet laddningar som ryms i kondensatorn vid en given spänning uttrycks som Q=C*U . När spänningen över kondensatorn ökar måste antalet laddningar öka i den enligt:

d(Q) =C*d(U)

Ökar antalet laddningar i kondensatorn, måste det gå en ström till kondensatorn enlig I = d(Q) / d (t)

Vi kombinerar d(Q) = C*d(U) med I = d(Q) / d(t) och får:

I= C*d(U)/(d)t, eller I=C*d(U) / d(t)

Här ser vi att ju större derivatan d(U)/d(t) över kondensatorn är desto, större blir också strömmen över den. Det är så kondensatorn i ett spänningsdelarfilter "ser" på studs att frekvensen ökar.

Det här var det bästa sättet för mig att förstå hur ett delningsfilter fungerar. En kondensator "ser" ju inte frekvens, för den har ju givetvis ingen aning om när en ökande sinuskurva ska påbörja sin färd nedåt igen. Det här känns inte som svart magi längre.

Derivatan av en sinuskurva med en viss amplitud är ett kapitel för sig, men fanns i b.la. Matte D gymnasiematteböcker för den som är intresserad.

[n3mmr]

Jag måste erkänna att jag öht inte begriper hur detta kan vara en fråga!

Det betyder antagligen att jag är lite konstig....

[Svante]

Derivatan av en sinuskurva med en viss amplitud är ett kapitel för sig, men fanns i b.la. Matte D gymnasiematteböcker för den som är intresserad.

Ja, d/dt (A*sin(wt))=A*w*cos(wt), dvs ju högre frekvens, desto större amplitud. w hoppar ut ur sinusen eftersom w är den inre derivatan. I detta fall betyder det att det blir mer ström genom kondensatorn om frekvensen är hög.

[Loud]

Jag måste erkänna att jag öht inte begriper hur detta kan vara en fråga!

Det betyder antagligen att jag är lite konstig....

Eller så har du likt dom flesta inte analyserat frågan ordentligt

[conny_a]

... fast egentligen finns ju inte DC. Det finns bara AC.

Tänk ett batteri på 9V. I början har det 0V - innan fabriken "laddat upp det". Sedan kopplar vi in det i en apparat och spänningen sjunker väldigt sakta ... tills det inte förmår hålla spänningen längre. Då sjunker spänningen igen. Långsamt .... en mycket långsam AC som inte hinner med en hel period ens ...

[Svante]

... fast egentligen finns ju inte DC. Det finns bara AC.

Tänk ett batteri på 9V. I början har det 0V - innan fabriken "laddat upp det". Sedan kopplar vi in det i en apparat och spänningen sjunker väldigt sakta ... tills det inte förmår hålla spänningen längre. Då sjunker spänningen igen. Långsamt .... en mycket långsam AC som inte hinner med en hel period ens ...

...fast perioden har en DC-komponent. Den är medelvärdet av spänningen under tiden. Dessutom har den en AC-komponent, som består av flera frekvenser.

DC-komponenten kan fö ses som en cosinus med frekvensen och fasläget noll.

[conny_a]

Över årmiljarderna har medelvärdet av spänningen i all världens utrustningar varit ganska låg, typ "summa spänning över 100 år" / några miljarder.

Men det är klart, i praktiska tillämpningar brukar DC vara ett bra begrepp när man pratar om en spänning som är konstant under den relevanta tiden.

Edit: Bör förtydliga att det är en utrustning i taget ... annars blir man mörkrädd ...