Konjugatlänkar Hur funkar dem?

[Svante]

Summan av två impedanser?!? Men de sitter ju i parallell! Och hur får man in konjugatregeln i resonemanget?

Det är väl snarare summan av överföringsfunktionerna för lågpass- och lågspärrfiltret som är konstant, och lika med Re.

Men, hur är de filter, menar du? Vad är insignal och vad är utsignal (för det har ju alla filter)? Menar du att spänning är insignal och ström i de två grenarna är utsignal?

Jag är helt med på att strömmarna summerar till U/R, och jag begriper helt och fullt hur man beräknar värdena och hur det fungerar. Jag är bara förbryllad över "konjugat", eftersom jag alltid har trott att det har rört sig om att impedanserna är varandras komplexkonjugat.

Hur får man in konjugatregelen i resonemanget?

Den som minns sin matematik inser omedelbart att summan av två impedanser som beskriver varandras konjugat, naturligtvis blir en rent resistiv last (skolexempel på utnyttjande av konjugatregeln ).

(Min fetstil)

Nja, jag trodde nog själv att den skulle vara med någonstans och blev styrkt av IÖ.

[phon]

Men, hur är de filter, menar du? Vad är insignal och vad är utsignal (för det har ju alla filter)? Menar du att spänning är insignal och ström i de två grenarna är utsignal?

Jaaa .... vad är det man skall lägga ihop egentligen? Nu tänker jag, vilket vanligen inte brukar hjälpa särskilt mycket

... men det verkar väl bra att ha strömmen som utsignal, och lägga ihop dom två strömmarna med fasvinkel och allt, så får man en konstant total ström med vinkel 0 som resultat ....


.... å spänning genom ström blir ju .... alltså, man lägger väl då ihop impedanserna istället, så blir resultatet en konstant resistans över frekvensen.



åsså var det den här konjugatregeln då ... den har nog bara lånat sitt namn av conjugare den också, inget att hänga upp sig på.

Dom är troligen kusiner på långt håll, konjugatregeln och konjugatlänken .... det hörs ju på namnet ... IÖ hjälp till nu ...


-

[d_anders]

Om du skriver om uttrycket för impedansen lite så kommer du ju att få (R+jwL)*aX, där X utgör konjugatet till R+jwL. Är det inte därifrån namnet konjugatlänk kommer?

[Svante]

Om du skriver om uttrycket för impedansen lite så kommer du ju att få (R+jwL)*aX, där X utgör konjugatet till R+jwL. Är det inte därifrån namnet konjugatlänk kommer?

Hurdå, kan du inte skriva ut det, pliis? Om X är komplexkonjugatet till (R+jwL) så är det ju (R-jwL). Och om Z ska bli R så måste a vara R/(R^2+(wL)^2).

Så (R+jwL)*a*X = (R+jwL)*(R-jwL)*R/((R^2+(wL)^2)=R

Men jag ser fortfarande inte hur de delarna kommer från kretsen.

När jag bollar formlerna får jag inte (R-jwL) utan (R-j/wC), dvs w står i nämnaren och då är uttrycken inte varandras konjugat vid alla w.

Om Zc=(R-j/wC) och Zl=(R+jwL) så blir ju hela kretsens impedans

Z=Zc Zl/(Zc+Zl) så det finns en multiplikation av impedanserna med där, som ju ger något som är besläktat med konjugatregeln. Närmare än så kommer jag inte.

Jaja, det är kanske dags att inse att min illusion om att det var komplexkonjugaten av impedanserna man avsåg, var just en illusion, och att termen "konjugatlänk" är påhittad på ett mer filosofiskt plan. Fast jag skulle vilja ha en kommentar av IÖ också, han verkade ju så tvärsäker på det där. Jag var också tvärsäker, men klarar inte att förklara det som jag var tvärsäker på. Gnurf!

[d_anders]

Ja alltså, om du skriver om uttrycket för den totala impedansen Z
så kommer du att få (R+jwL)*a*(R-jwL), givetvis förutsatt att du har valt L,C och Ri:na rätt. a blir ett reellt uttryck.

Jag vet inte om mina omskrivningar var onödigt krångliga, men de blev någon meter. Om du vill kan du ju göra ett speciallfall, t ex Ri=1, L=C. Då bör du få Z=(1+jwL)(1-jwL)/(1+w^2*L^2). Att det går är ju ett måste i och med att Z blir reellt.

Jag är fortfarande inte säker på om jag har förstått dig rätt. Om du utgår från Z1=R1+jwL så ska det ju multipliceras med sin konjugat för att bli reellt, dvs Z2/(Z1+Z2) ska vara ett reellt tal multiplicerat med Z1:s konjugat.

[IngOehman]

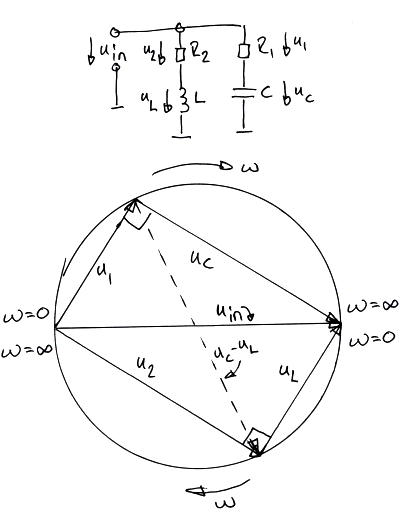
Men, hur är de filter, menar du? Vad är insignal och vad är utsignal (för det har ju alla filter)? Menar du att spänning är insignal och ström i de två grenarna är utsignal?

Jaaa .... vad är det man skall lägga ihop egentligen? Nu tänker jag, vilket vanligen inte brukar hjälpa särskilt mycket

Det är nog jag som uttryckt mig slarvigt redan i det första inägget.

När jag skrev "summan av impedanserna" så borde jag kanske för tydlighetsskull ha skrivit "summan av impedansernas belastning". Då hade det blivit mera lättläst/begripligt. Det är ju den komplexa konduktiviteten (admittanserna) man summerar, inte den komplexa impedansen. Om man skall vara noga. Och det skall man förstås alltid vara, där man inte specifikt reserverar sig för att man inte är det.

Sorry alltså för min slarviga formulering.

åsså var det den här konjugatregeln då ... den har nog bara lånat sitt namn av conjugare den också, inget att hänga upp sig på.

Dom är troligen kusiner på långt håll, konjugatregeln och konjugatlänken .... det hörs ju på namnet ... IÖ hjälp till nu ...

Jo, alltså, allt det där har man kunnat läsa om i detalj i MoLt (där jag, till skillnad från här, tänkt igenom det hela innan jag skrev något...), men en snabbis kommer här:

Konjugatregeln säger att när man multiplicerar ihop två grunkor av formen (A-B) * (A+B) så får man A^2 + AB - AB - B^2, vilket kan förkortas till A^2 - B^2.

[edit: Nu har jag läst igenom förra sidan också, det som skrevs när jag varot borta några timmer... Och jag inser att det alldeles ovanstående är en meninglös repetition av saker som redan sades på förra sidan. Men, jag låter det stå kvar ändå.]

Nu förenklar jag illa mycket: Grejjen med det hela är att de där mellanlänkarna är de reaktiva komponenterna, där den ena är "reaktivt positiv" medan den andra är "reaktivt negativ". Väljer man rätt värden på alltihopa återstår bara den realla delen! Resistansen alltså.

I verkligheten så kan konjugatlänkar (inte leksakskonjugatlänkar då alltså från "högtalarräknestickor") bestå av massor av komponenter, beroende på hur impedansen, vars matematiska konjugat man söker, ser ut.


Vh, iö


Håller verkligen med Svante om att en konjugatlänk inte är ett filter, den har ingen transmissions-överföringsfunktion, bara en belastningsfunktion. Däremot kan konjuatlänkar förstås ingå i filter, och synnerligen påverka filtrets överföringsfunktion. Men i vissa fall påverkar de inga överfföringsfunktioner alls, utan finns där bara för att minska impedansens fasvinkel.

Det kan nämnas att i enfrekvensiga sammanhang (nätspänningssammanhang t ex) finns det betydligt bättre sätt att fixa till fasvinklar än med konjugatlänkar. De senare ställer ju alltid till med en energiomvandlingsprocess, på grund av sin reella komponent. Effektslöseri med andra ord. Det vill man inte ha i nätspänningssammanhang, så där faskompenserar man med fördel rent reaktivt, vilket även i det fallet leder till en rent resistiv last, men bara smalbandigt - alltså vid en enda frekvens.

[Svante]

Jag är fortfarande inte säker på om jag har förstått dig rätt. Om du utgår från Z1=R1+jwL så ska det ju multipliceras med sin konjugat för att bli reellt, dvs Z2/(Z1+Z2) ska vara ett reellt tal multiplicerat med Z1:s konjugat.

Så, du menar att Z2/(Z1+Z2), eller Zc/(Zc+Zl) som jag kallade det är själva konjugatet som har gett namnet? Hmm.

Ja Zc/(Zc+Zl)=(R+1/sC)/(2R+sL+/sC) och C=L/R² som du sa förut, så uttrycket blir (R+R²/sL)/(2R+sL+R²/sL)=(sLR+R²)/(2RsL+s²L²+R²)=R (R+sL)/(R+sL)², vilket multiplicerat med (R+sL) förstår blir R. Så visst måste Zc/(Zc+Zl) vara komplexkonjugatet till Zl.

Visst är det så, men är inte det en lite långsökt tolkning? Bäst hittills dock .

[d_anders]

Jag tänker lite trögt när det är varmt. Om du parallellkopplar Z med dess konjugat Z' så kan man ju direkt beräkna den totala impedansen till Z*Z´(Z+Z´)=|Z|^2/(2*Re(Z)).

[Svante]

Jag tänker lite trögt när det är varmt. Om du parallellkopplar Z med dess konjugat Z' så kan man ju direkt beräkna den totala impedansen till Z*Z´(Z+Z´)=|Z|^2/(2*Re(Z)).

Ja, men nu är det ju inte det man gör. (R+1/sC) är inte konjugatet till (R+sL)

[Morello]

Jag tänker lite trögt när det är varmt. Om du parallellkopplar Z med dess konjugat Z' så kan man ju direkt beräkna den totala impedansen till Z*Z´(Z+Z´)=|Z|^2/(2*Re(Z)).

Ja, men nu är det ju inte det man gör. (R+1/sC) är inte konjugatet till (R+sL)

Exakt.

Kanske kommer benämningen konjugatlänk från det faktum att de tvenne grenarna är varandras konjugat vid exakt en frekvens?

[Svante]

Jag tänker lite trögt när det är varmt. Om du parallellkopplar Z med dess konjugat Z' så kan man ju direkt beräkna den totala impedansen till Z*Z´(Z+Z´)=|Z|^2/(2*Re(Z)).

Ja, men nu är det ju inte det man gör. (R+1/sC) är inte konjugatet till (R+sL)

Exakt.

Kanske kommer benämningen konjugatlänk från det faktum att de tvenne grenarna är varandras konjugat vid exakt en frekvens?

Undrar vad det var för en tossig namnpåhittare då. Det är ju inte intressant. Det är ju för alla frekvenser det ska bli resistivt.

[IngOehman]

Jamen det blir det ju också!

En konjugatlänk är ju en länk som vid varje frekvens uppvisar det matematiska konjugatet till ursprungsimpedansen.

Jag tror man kan säga såhär:
Det finns massor av tänkbara parallellimpedanser (oändligt många faktiskt!) som med hjälp av konjugatregeln kan påvisas eliminera de reaktiva elementen hos ursprungsimpedansen vid en given frekvens (alltså om man utgår ifrån impedansens uttryck vid en given frekvens), men det finns bara en av dessa tänkbara "med konjugatregeln påvisbara" användbara parallellimpedanserna, som "trackar" originalimpedansen, såtillvida att det vid alla frekvenser medelst konjugatregeln kan påvisas eliminera originalimpedansens reaktiva del.

Tricket är att hitta den!
Och när man gjort det så utropar man: Yeah! De' kallar jag en konjugatlänk!

(Jag beskrev det hela mycket bättre i MoLt för en massa år sedan... Har jag för mig. Någon som kan hitta? Jag tror det var i samband med filtergenomgången av antingen den gamla LTS-tvåvägaren, eller den senare trevägaren.)


Vh, iö

[d_anders]

Jo, man kan välja det till det komplexa konjugatet, men det är inte nödvändigt att göra det.

Edit: Nu tänkte jag bara matematiskt, ni har rätt.

[Morello]

En konjugatlänk till

Z=R+sL

är

Zk=R+1/sC

men Zk är konjugatet till Z(dvs Z=Z*) om och endast om sL=-1/sC, dvs endast vid vinkelfrekevensen w=1/rt(LC).

[Svante]

Jamen det blir det ju också!

Nämen, blir det?

En konjugatlänk är ju en länk som vid varje frekvens uppvisar det matematiska konjugatet till ursprungsimpedansen.

Hmm, och vad är det matematiska konjugatet till R+jwL då? Det måste väl vara R-jwL?

Seriekopplar vi dem så blir impedansen 2R, resistivt och fint. Parallellkopplar vi dem blir impedansen visserligen resistiv, men inte konstant (den blir (R²+w²L²)/2R). Dessutom är impedansen R-jwL instabil, så hur vi än vrider och vänder uttrycken för RC-länken så är det inte den vi har för den impedansen är ju stabil.

Eller menar du att det matematiska konjugatet till admittansen för R+jwL ? Admittansen är ju 1/(R+jwL) = (R-jwL)/(R²+w²L²)

Konjugatet till den är (R+jwL)/(R²+w²L²). Kopplar vi dem i parallell så får vi admittansen (R+jwL)/(R²+w²L²)+(R-jwL)/(R²+w²L²)=(2R)/(R²+w²L²). Den är också rent resistiv, men inte frekvensoberoende. Dessutom är även admittansens konjugat instabilt. NoGo.

Så jag skulle vilja att du förklarar det jag inte har förstått med

En konjugatlänk är ju en länk som vid varje frekvens uppvisar det matematiska konjugatet till ursprungsimpedansen.

med formler. Och vad är egentligen ett matematiskt konjugat? Termen "impedanskonjugat" var uppe nyss, jag har pratat om komplexkonjugat, och nu matematiskt konjugat. Är de olika?

[IngOehman]

Me' formler?

Nä, det skall va gött å leva, annars kan det kvetta.


Vh, iö

- - - - -

PS. Jag tror det är bra att bryta sig loss från formlerna och låta de elektriska händelserna flyta omkring liksom lite friare i hjärnan istället.

Då ser man kanske att L bara är en bokstav, förvisso illustrerande en sorts elektrisk förutsättning, men eftersom grundprincipen i mitt resonemang var att titta på en frekvens i taget (därmed behöver vi inte bry oss om frekvensberoendet, bara fasegenkaperna), men å andra sidan: Vi skall bara kalla den sak för konjugatlänk, som funkar vi alla frekvenser!

Då behöver man inte (bör inte) tänka i termer av bokstäver, utan i termer av värden (eller ännu hellre beteenden). Då ser man att det vid en given frekvens inte behöver bry sig om vad som heter L och vad som heter C - bara man byter tecken på imaginäriteten, så får man byta bokstav också!

Gör man inte det (byter tecken och bokstav) så kommer man inte upnå det man vill, nämligen att hitta ett uttryck som "trackar" det man vill göra reellt, alltå... reellisera (heter det så?).

[Svante]

OK, men du kan väl tala om vad du menar med matematiskt konjugat? Är det ett komplexkonjugat, dvs att imaginärdelen har bytt tecken?

[Morello]

En konjugatlänk är ju en länk som vid varje frekvens uppvisar det matematiska konjugatet till ursprungsimpedansen.

Vh, iö

Jag tror det är ovanstående som Svante med emfas menar inte stämmer, vilket jag menar att han har rätt i.

[IngOehman]

OK, men du kan väl tala om vad du menar med matematiskt konjugat? Är det ett komplexkonjugat, dvs att imaginärdelen har bytt tecken?

Nä, egentligen inte.

Jag menar nog att konjugatet är det uttryck som, frekvensoberoende, alltid eliminerar imaginärdelen. Det kanske borde kallas komplettkonjugatet?

Det betyder att det inte går att sätta upp en ekvation där man har med saker som i verkligheten är variabler (typ s). För med sL på plats går ju s åt fel håll i den konjugerade halvan om man ser det så. Byter man L mot 1/C däremot... Fast en korrektion för att R i förekommande fall avviker från 1 ohm måste förstås in också.

Nä, det jag skrev i MoLt var fortfarande MYCKET bättre. Har jag för mig.


Vh, iö

[d_anders]

Jeg håller nog också med, förutsatt att länken ska vara fysiskt realiserbar med endast ett motstånd och en kondensator.

[Svante]

OK, men du kan väl tala om vad du menar med matematiskt konjugat? Är det ett komplexkonjugat, dvs att imaginärdelen har bytt tecken?

Nä, egentligen inte.

Jag menar nog att konjugatet är det uttryck som, frekvensoberoende, alltid eliminerar imaginärdelen. Det kanske borde kallas komplettkonjugatet?

Hmm, undrar om det någonsin, någonstans i hela världen finns någon som har använt den definitionen av "matematiskt konjugat".

Nåja, nu ska jag sova, gonatt!

[IngOehman]

Någon gång skall vara den första!


Å andra sidan är det ju som så, att konjugatregeln inte har något definierat specialfall för stabilisering av ihopmultiplicering av två uttryck där saker skall gå ihop även om man i båda termerna har en variabel ingömd, som skall tillåtas att variera (s)?


Å tredje sidan kanske jag bara försöker luras?

Det kanske varken handlar om komplexkonjugat eller komplettkonjugat, utan om komplottkonjugat!!!


Vh, iö

[phon]

Håller verkligen med Svante om att en konjugatlänk inte är ett filter, den har ingen transmissions-överföringsfunktion, bara en belastningsfunktion. Däremot kan konjuatlänkar förstås ingå i filter, och synnerligen påverka filtrets överföringsfunktion. Men i vissa fall påverkar de inga överfföringsfunktioner alls, utan finns där bara för att minska impedansens fasvinkel.

Håller också med, det är inga filter, men om man ser de två länkarna som filter, tar ut spänningen över C resp L, och sedan adderar de båda graferna, så blir resultatet ett rakt streck vilket jag då tänkte skulle visa att konjugatlänken fungerar oberoende av frekvensen. Förutsatt att den är rätt vald map Le och Re förståss.

[Svante]

Kom just att tänka på en relaterad sak, som jag bara inte kan motstå att lägga upp. Hittills har vi ju faktiskt lyckats hålla oss on-topic, så man får väl göra vad man kan för att ändra på det.

Om man tager sig en RL-länk i parallell med en RC-länk, och ritar upp vektorerna i det komplexa talplanet för spänningarna som finns i schemat så blir de så här:



Inspänningen uin är hela tiden referensen, och därför ligger den vågrätt till höger och är alltid lika lång. Sedan inser man att summan av u1 och uc är just uin. Vidare inser man att u1 och uc ligger 90° ur fas och att uc ligger efter u1. Ritar man upp vektorerna så inser man att knutpunkten i vilken u1- och uc-vektorerna summeras kommer att ligga på en cirkelbåge, eftersom vinkeln mellan dem är rät. För låga frekvenser hamnar nästan hela spänningen över C och för höga hamnar allt över R1. Därför kan vi göra en frekvensskala längs cirkelbågen med 0 längst till vänster och oändligt längst till höger.

För RL-länken gäller nästan samma sak, men eftersom spänningen ul ligger 90° före u2 så kommer den knutpunkten att vandra på den nedre cirkelhalvan, fortfarande med ökande frekvenser medsols.

Effekten som utvecklas i R1 blir u1²/R1 och effekten som utvecklas i R2 blir u2²/R2. Om R1=R2=R så kommer den totala effekten som utvecklas i de två motstånden att vara (u1²+u2²)/R.

Om dessutom de två knutpunkterna rör sig diametralt motsatt kommer u1 och u2 att ligga vinkelrätt mot varandra. När frekvensen ändras kommer sqrt(u1²+u2²) att vara cirkelns diameter, dvs beloppsmässigt lika med uin. Alltså kommer den totala effekten som utvecklas i R1 och R2 alltid att vara (u1²+u2²)/R=uin²/R, vilket får en att ana att lasten som uin ser är just R. Oberoende av frekvens.

En annan intressant sak är spänningen uc-ul, alltså skillnaden mellan spänningarna i mittpunkterna. Sett relativt inspänningen kommer den att ha en allpasskaraktär, vi kan se att den alltid är beloppsmässigt lika stor, men att den vrider sig. Det betyder att uc-ul ligger i fas vid låga frekvenser och ur fas vid höga frekvenser. Ett allpassfilter, mao.

Allt under förutsättning att brytfrekvenserna i RL- och RC-länkarna är lika, dvs w0=1/RC och w0=R/L, dvs R/L=1/RC eller R²C=L.

Fanastiskt vad man kan rita med vektorer ibland... Och attans det blev ju nästan on-topic igen. Det måste ha varit något fundamentalt intressant med frågan...

Men komplexkonjugatet är ju lysande. Med sin frånvaro.

[phon]

Tjusigt! Det är ju mina "filter" som jag tänkte det, fast det här var ju attans mycket bättre beskrivet!

[Svante]

Ska vi titta på konsekvenserna i verkliga (hrrmm, nåja simulerade, men verkligare) fall också?



I simuleringen nedan finns det fem olika system. Det är två olika högtalarelement, ett "blått" och ett"rött". Det blåa elementet är någorlunda verklighetsnära, dvs det har en talspoleinduktans med förluster. Det röda har en skolbokstalspoleinduktans med Z=jwL. Sådana element är ytterst ovanliga i verkligheten, men det är sådana som hela teorin med konjugatlänkar som vi har diskuterat handlar om.

Impedanserna för de två elementen visas dels utan konjugatlänk (heldragen), dels med konjugatlänk (kortstreckad). Sista (långstreckade) impedanskurvan kommer jag till snart.

Om vi räknar ut konjugatlänken riktigt till det röda systemet så blir impedansen helt resistiv och konstant för höga frekvenser. Skolbok.

Kopplar vi samma konjugatlänk till det blåa systemet, så blir det inte lika jämnt, det finns fortfarande en viss ojämnhet i impedanskurvan, även om den är jämnare än utan länk.

Om man pillar lite med R och C i konjugatlänken så kan man komma fram till något som är jämnare, tex den långstreckade kurvan. Det brukar bli R- och C-värden som är större än vad de blir när man bara räknar. Därför brukar ibland tillverkarna föreslå värden på R och C i konjugatlänken och R är då nästan alltid högre än talspoleresistansen (vilket den som just har förstått teorin med konjugatkompensering lätt finner förbryllande). Hursomhelst, helt plan blir kurvan inte.

Vi kan även notera att det bara finns två tonkurvor i bilden. Det beror på att elementet drivs av en ideal förstärkare. I verkliga livet sitter det ju ett delningsfilter mellan förstärkaren och elementet, och eftersom delningsfiltret känner olika last för de olika systemen, så kommer spänningen från filtret att vara olika för systemen. Mao, om det hade varit ett delningsfilter med i bilden, så hade vi haft fem olika tonkurvor.

Eftersom det är enklare att dimensionera ett filter för konstant lastimpedans, så används konjugatlänkar för att "få till" tonkurvan utan alltför mycket provande eller simulerande. Ibland behövs de, ibland klarar man sig utan.

Till sist ser vi också att den enkla RC-konjugatlänken inte kompenserar bort systemresonansen vid 35 Hz. Den tar bara hand om talspoleinduktansens påverkan på impedansen. Systemresonansen behöver sällan kompenseras bort, i varje fall för baselementet, delningsfrekvensen (där det är mest kritiskt med konstant resistiv impedans) ligger ju i ett helt annat frekvensområde.

[Morello]

Vill lite försiktigt påpeka att man ytterst sällan behöver tillgripa länkar som plattar till impedansen. Det finns så att säga inget axiom som säger att det är en fördel. Det är snarast något av en dogm att man först, utan att beakta hela systemet, skall tillse en resistiv last för filtret.

[Svante]

Vill lite försiktigt påpeka att man ytterst sällan behöver tillgripa länkar som plattar till impedansen. Det finns så att säga inget axiom som säger att det är en fördel. Det är snarast något av en dogm att man först, utan att beakta hela systemet, skall tillse en resistiv last för filtret.

Nävisst! Det är ett knep som man kan ta till om det behövs, tex för att få filtret att uppföra sig som man vill. Det kan gå mycket bra på andra sätt också, ofta kan talspoleinduktansen tom ses en del av filtret.

[Flint]

Vill lite försiktigt påpeka att man ytterst sällan behöver tillgripa länkar som plattar till impedansen. Det finns så att säga inget axiom som säger att det är en fördel. Det är snarast något av en dogm att man först, utan att beakta hela systemet, skall tillse en resistiv last för filtret.

Nävisst! Det är ett knep som man kan ta till om det behövs, tex för att få filtret att uppföra sig som man vill. Det kan gå mycket bra på andra sätt också, ofta kan talspoleinduktansen tom ses en del av filtret.

Det ni säger nu tycker jag stämmer om man håller sig till filter med lägre ordningstal men när det gäller 12dB, 18dB och Linkwitz kan det bli himla gropigt utan konjugatlänkar.

[Svante]

Vill lite försiktigt påpeka att man ytterst sällan behöver tillgripa länkar som plattar till impedansen. Det finns så att säga inget axiom som säger att det är en fördel. Det är snarast något av en dogm att man först, utan att beakta hela systemet, skall tillse en resistiv last för filtret.

Nävisst! Det är ett knep som man kan ta till om det behövs, tex för att få filtret att uppföra sig som man vill. Det kan gå mycket bra på andra sätt också, ofta kan talspoleinduktansen tom ses en del av filtret.

Det ni säger nu tycker jag stämmer om man håller sig till filter med lägre ordningstal men när det gäller 12dB, 18dB och Linkwitz kan det bli himla gropigt utan konjugatlänkar.

Jajustdet, man tar till det om det behövs. Och det är troligare att det behövs vid högre ordningar och skolboksdimensionering av filtren. Observera att jag inte lägger något värde i de orden, jag menar inte att konjugatlänkar per definition är vare sig bra eller dåliga eftersom de kan vara bådadera. De är verktyg som man kan ta till just om de behövs.