Bra jobbat
/Johan
Moderator: Redaktörer
Mig själv skrev:Summering av kommande steg:
1: Tillse att diffusorplattan kommer närmre domen (ca 1,2 mm)
2: Borra hål i diffusorplattan.
3: Göra en liten större diffusorplatta och i steg gå från att borra ett litet hål till större hål.
4: Brantare vinkel i innerdel (den övre varianten i bild ovan, fast kanske ännu lite brantare i innerdel och flackare i ytterdel)
5: Lägre profil och mindre diameter (skala ner från 150 mm till 100-120 mm. (Den undre varianten i bild ovan).
Förhoppningsvis räcker dessa steg. Purifis mer avancerade lösning ger fler variabler och är därmed krångligare att få till utan avancerad simulering.
However, in order to have 94dB SPL hitting your ear from, say, 2m distance, we need a much higher SPL locally at the radiator surface. This is where the radiating area matter a lot: it takes a given volume displacement (or rather volume acceleration, to be precise) to reach 94dB at 2m distance...
Now, at such high SPL, the air is noticeably nonlinear. ..
Such a nonlinear relationship creates harmonic distortion, mainly 2nd harmonics but also a little bit of higher harmonics. In fact, most good tweeters have their 2nd harmonic distortion limited by this fundamental mechanism. Comparing same-sized tweeters at the same SPL reveals a shockingly consistent lower floor of the 2nd harmonic distortion. This is to be blamed on our atmosphere rather than the tweeter it self. For some reason, this has remained a well-kept secret.
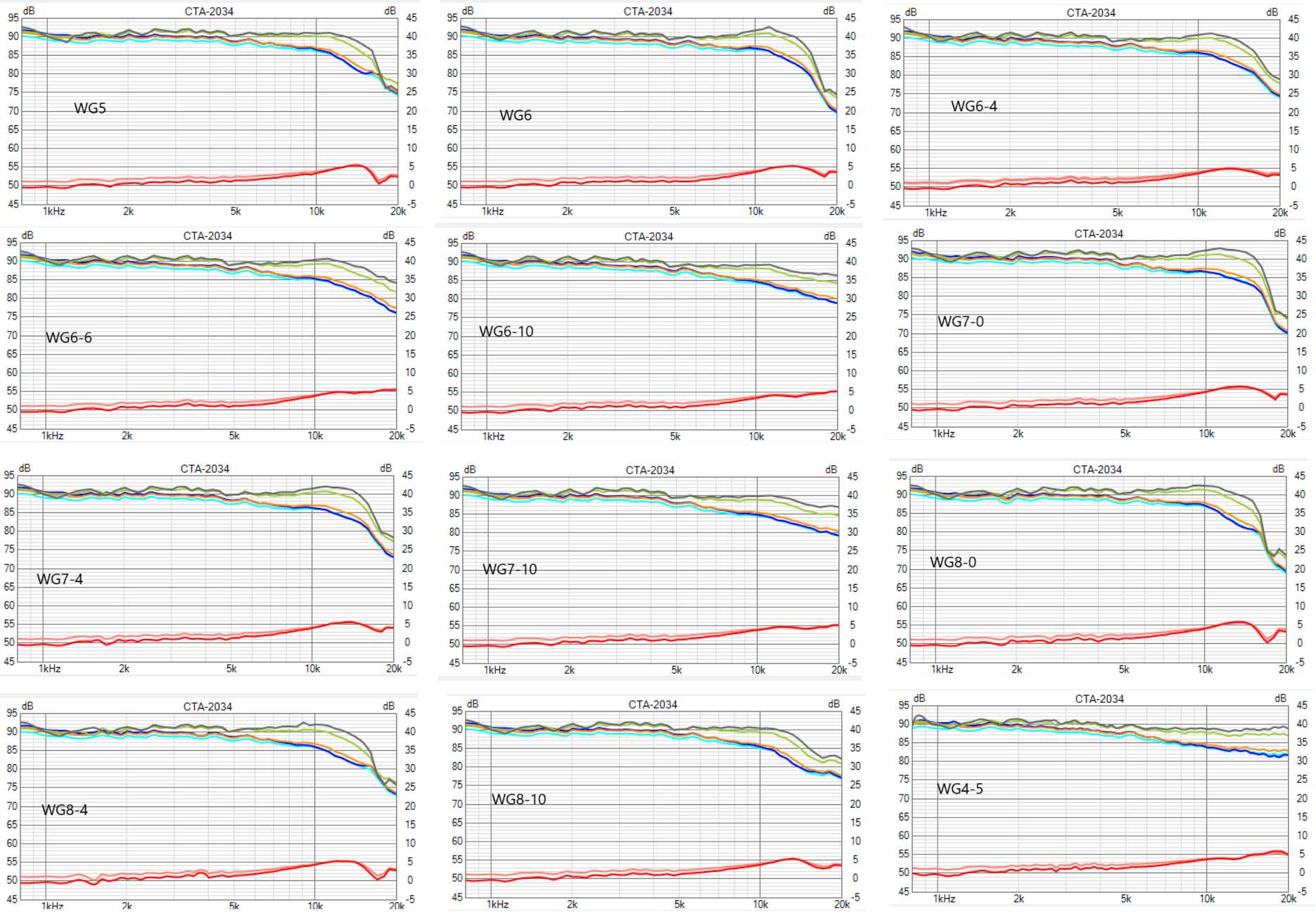
Maarten skrev:Så här ser Johan's senaste mätningar ut jämfört mot den första samt även den djupare TW29 med och utan vågledare:
Alla dessa har DI runt 5 i översta diskanten, vilket nog kommer att motsvara ett DI om 10 när man mäter full Spinorama, dvs hela varvet (360 grader).
Så än så länge ingen vinst där men en stor vinst med hög känslighet och utjämnad frekvensgång. Räv-L-baffel kommer inte att behövas med denna vågledare.
Här är en uppdaterad bild på hur profil och frekvensrespons i referensaxel hänger ihop. Det som inte är med är spridningen och man kan anta att den är inversen av vågledareffekten i referensaxeln (HOR 0), dvs, ju mer lyft vågledaren ger, desto mer riktad och mindre spridning.
...
Uppföljning och fortsättning:Mig själv skrev:Summering av kommande steg:
1: Tillse att diffusorplattan kommer närmre domen (ca 1,2 mm)
2: Borra hål i diffusorplattan.
3: Göra en liten större diffusorplatta och i steg gå från att borra ett litet hål till större hål.
4: Brantare vinkel i innerdel (den övre varianten i bild ovan, fast kanske ännu lite brantare i innerdel och flackare i ytterdel)
5: Lägre profil och mindre diameter (skala ner från 150 mm till 100-120 mm. (Den undre varianten i bild ovan).
Förhoppningsvis räcker dessa steg. Purifis mer avancerade lösning ger fler variabler och är därmed krångligare att få till utan avancerad simulering.
Punkt 1-3 klara och de blev som vi hoppades på. Punkt 4 och 5 modifieras en smula till att innefatta en yttre ring á la Purifi och höja profilen något i mellandelen för att öka på nivån och minska spridningen i registret 1- 6 kHz.
Samt:
6: Minska ner mitthålet från 6 mm till 3-4 mm.
7: Testa med varianter av lite svagare vinkel i innersta delen då vi nu fått upp nivå med mittpluppen.
T ex så här (med varianter):






Menar du såhär? Kladdade på telefonen men jag hoppas du förstår.Chris71 skrev:Fantastiskt bra kämpat, nu har jag inte följt varenda inlägg men har det gjorts någon modell som börjar med 90grader i halsen direkt mot frontplattan eller har alla börjat sprida redan från botten i WG?

johaneriksson skrev:Menar du såhär? Kladdade på telefonen men jag hoppas du förstår.Chris71 skrev:Fantastiskt bra kämpat, nu har jag inte följt varenda inlägg men har det gjorts någon modell som börjar med 90grader i halsen direkt mot frontplattan eller har alla börjat sprida redan från botten i WG?
[ Bild ]
I-or skrev:En smalare hals ger mycket riktigt för höga frekvenser något högre nivå på axeln på bekostnad av mindre spridning.
Mig själv skrev:Summering av kommande steg:
1: Tillse att diffusorplattan kommer närmre domen (ca 1,2 mm)
2: Borra hål i diffusorplattan.
3: Göra en liten större diffusorplatta och i steg gå från att borra ett litet hål till större hål.
4: Brantare vinkel i innerdel (den övre varianten i bild ovan, fast kanske ännu lite brantare i innerdel och flackare i ytterdel)
5: Lägre profil och mindre diameter (skala ner från 150 mm till 100-120 mm. (Den undre varianten i bild ovan).
Punkt 1-3 klara och de blev som vi hoppades på.
Extra ring hjälpte ej: Punkt 4 och 5 modifieras en smula till att innefatta en yttre ring á la Purifi och höja profilen något i mellandelen för att öka på nivån och minska spridningen i registret 1- 6 kHz.
6: Minska ner mitthålet från 6 mm till 3-4 mm.
7: Testa med varianter av lite svagare vinkel i innersta delen då vi nu fått upp nivå med mittpluppen
Användare som besöker denna kategori: supra_jonny och 48 gäster