Tänker på denna
Moderator: Redaktörer

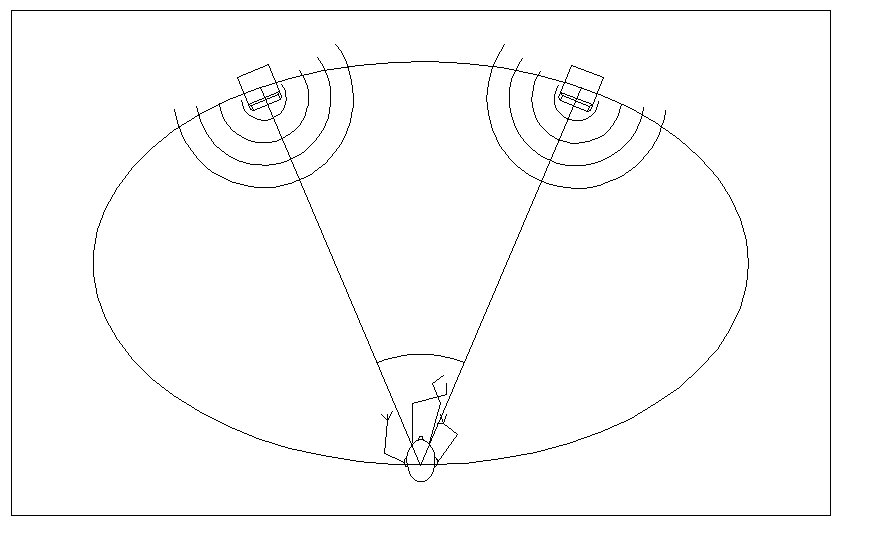
Rydberg skrev:Eftersom jag är lat och inte orkar tänka efter själv (inte idag iaf) så vill jag gärna ha en heltäckande beskrivning av hur man kom fram till avstånden? Hur man ska placera högtalarna och sig själv i förhållande till elipsen? etc. Sökte lite innan men hittade inte det jag sökte
Dahlqvist skrev:Jag vill minnas att Inos högtalare är konstruerade att placeras på rumsellipsen, medan Carlsson placeras utanför densamma.
Svante skrev:Alltså, informationen är inte tillräcklig. Har man tre punkter kan man alltid lägga en ellips igenom dem. Man kan tom lägga en cirkel igenom dem. Vad som saknas är hur ellipsen ligger i förhållande till rummet.
Audix skrev:Sedan bör man egentligen göra likadant med golv & tak. Dvs det blir något eggformat i slutänden.
E skrev:Man kan ta en liten anings mindre än 0,8 om man vill ha ellipsoidens horisontella tvärsnitt (ellipsen) vid den ungefärliga höjd över golvet som öronen råkar befinna sig, vilket ju oftast är under halva takhöjden. De som har högt i tak brukar sitta väsentligt lägre - relativt mitten alltså! Man kan förstås räkna ut det också om man vill vara noga...
Sedan får man ju inte glömma att ellipsen påverkas kraftigt av väggarnas beskaffenhet, ju mjukare väggar desto mer rumsellipsdist. Öppna gluggar vädrar ut basen effektivt.
Mvh E*
IngOehman skrev:E skrev:Man kan ta en liten anings mindre än 0,8 om man vill ha [...] under halva takhöjden. [...]
Det kanske man skulle kunna tro, men det har jag faktiskt tagit hänsyn till redan.Annars (på halvhöjd) skulle det snarare vara 0,9.

zvenzzon skrev:Då fås:
x = cos(r)*Xradie
y = sin(r)*Yradie
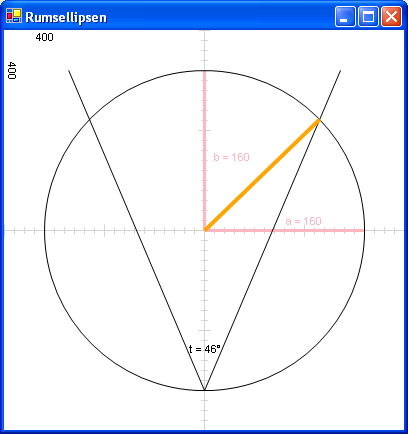
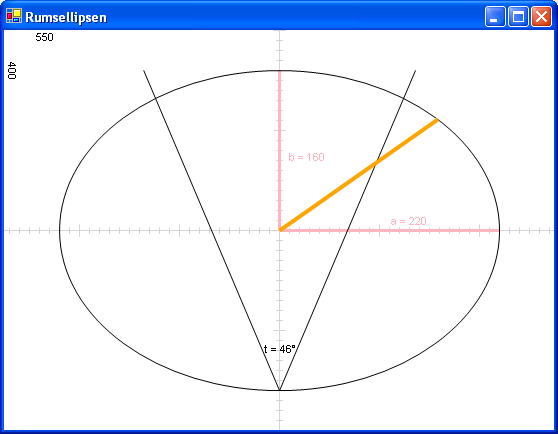
E skrev:I rummet som illustreras i din sista bild så flyttar man lämpligen bak
och ihop högtalarna
Svante skrev:Man får välan ordna med två ekvationer, en som beskriver ellipsen och en som beskriver linjen. Ur det borde skärningspunkterna trilla. Eftersom ellipsen beskrivs av en modifierad pythagoras med kavadrater och allt så borde det bli en andragradare att lösa.
bosco skrev:Svante skrev:Man får välan ordna med två ekvationer, en som beskriver ellipsen och en som beskriver linjen. Ur det borde skärningspunkterna trilla. Eftersom ellipsen beskrivs av en modifierad pythagoras med kavadrater och allt så borde det bli en andragradare att lösa.
Jag löste det till slut... var lite segt med algebran eftersom det är första gången sedan gymnasiet
Räta linjens ekvation och ellipsens ekvation likställs för y, då får jag x genom andragradaren:
(a2 · k2 + b2) · x2 + 2 · a2 · k · m · x = 0
och motsvarande för y:
(a2 · k2 + b2) · y2 - 2 · b2 · m · y + b2 · m2 - a2 · b2 · k2 = 0
Där k och m kommer från räta linjens ekvation och a och b är ellipsens större respektive mindre axel mätt från origo.
k = tan(90 - (46/2)) för en 46-gradig vinkel från lyssnaren och m = -b
E skrev:15 år gammal tråd!
Mvh E*
Ronnie skrev:
Verkar flott, men den där går inte att köra på mac va?
Nattlorden skrev:Ronnie skrev:
Verkar flott, men den där går inte att köra på mac va?
Inte om det är en så kass mac att den inte kör pc-program, nej.
Någongång i någon obekant framtid kanske den går att skriva om på ett sätt som kör i webläsare... men är inte ännu kunnig i något system som fixar det och som jag skulle trivas att lära mig.
( Blazer kanske kan vara något om det håller när man skrapat på ytan..... får se... )
hifikg skrev:Alla macar kan agera bättre PC än vilken PC som helst, men varför!?
Ronnie skrev:E skrev:15 år gammal tråd!
Mvh E*
Ja, men Bosco verkar leva fortfarande!
Laddade ner en app som verkar kunna rita upp sånt där; GoeGebra. Måste dock lära mig lite matematik om jag ska komma nån vart.
bosco skrev:Blev så exalterad av att remastern av Porcupine Trees "In Absentia" har mer dynamik än originalet att jag ville se om någon snappat upp det på faktiskt.Steven Wilson går från klarhet till klarhet.
Almen skrev:bosco skrev:Blev så exalterad av att remastern av Porcupine Trees "In Absentia" har mer dynamik än originalet att jag ville se om någon snappat upp det på faktiskt.Steven Wilson går från klarhet till klarhet.
Surely you jest, Sir?!?!?!?!? Nu blev ju jag intresserad av en remaster ffg på länge.
mrGaskill skrev:För väldigt länge sen vurmade jag för SW/PT och IA DVD-a. Inte så många intresserade då. Men DVD-a lät ju lite väl diskantrik.
goat76 skrev:Almen skrev:bosco skrev:Blev så exalterad av att remastern av Porcupine Trees "In Absentia" har mer dynamik än originalet att jag ville se om någon snappat upp det på faktiskt.Steven Wilson går från klarhet till klarhet.
Surely you jest, Sir?!?!?!?!? Nu blev ju jag intresserad av en remaster ffg på länge.
Det verkar stämma enligt Dr. Loudness. http://dr.loudness-war.info/album/list? ... n+Absentia
Hoppas nu bara normaliseringar hos streamingtjänsterna börjar locka fram allt fler nya remasters på tidigare sönderkomprimerade verk, och att allt fler nyproducerade skivor får behålla sin dynamik.
Användare som besöker denna kategori: Inga registrerade användare och 49 gäster