Jag roade mig med att dels försöka hitta på en formel själv, dels att försöka skriva formlerna i tråden på samma form, så att man kan jämföra dem.
Jag gillar ju när det finns en teoretisk grund till formler och en sådan tänkbar grund är en Butterworthdimensionering, dvs att tonkurvan är maximalt platt ovanför en viss brytfrekvens och att den faller (brant) därinunder. Om man antar att lådan är förlustfri, ställer det ganska kinkiga krav på elementet och låda, nämligen att
fp=fs
Vb=Vas/1,414
Dessutom måste elementet ha Qts=0,38
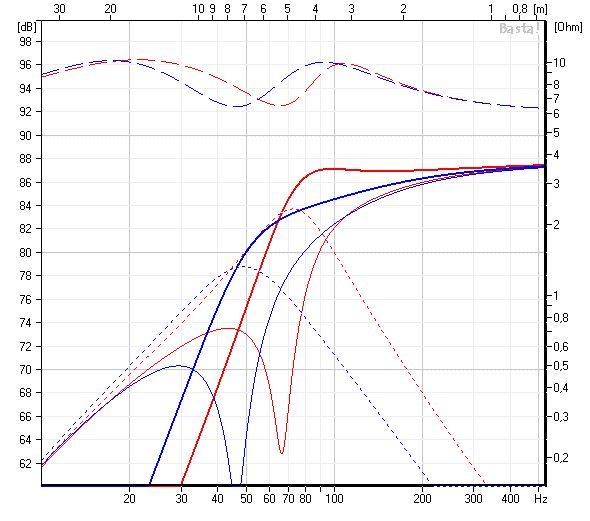
Om nu inte elementet har det Qts-värdet då? Vad gör en stackars teoretiker? Då kom jag ihåg observationen som vi gjorde i en tredje tråd, nämligen att Cms inte spelar sådär hemskt stor roll för den slutgiltiga tonkurvan. I den tråden lade jag upp den här bilden:
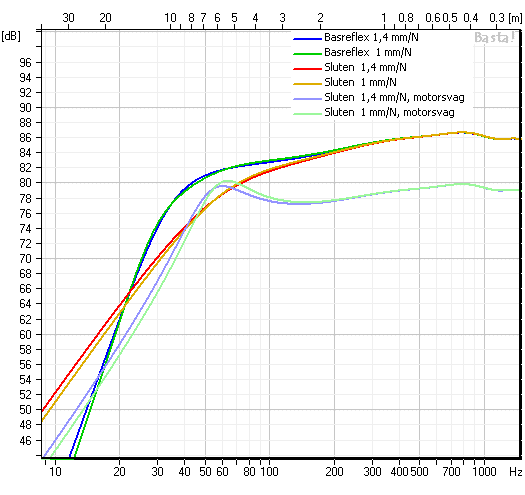
Här varierar Cms ganska mycket men tonkurvan blir nästan samma i alla fall. Nå, eftersom både fs och Qts beror på Cms, så kan jag alltså låtsas att elementet har en Cms som gör att Qts blir 0,38, då skulle jag ju få en nära-Butterworthdimensionering.
fs=1/(2*pi*sqrt(Mms*Cms))
Qts=sqrt(Mms/Cms)/Rms
Först hittar man alltså på ett nytt Cms' som gör att ett nytt påhittat Qts' blir 0,38
Cms'=Mms/(Rms²*Qts'²)
...och så stoppar man in det i formeln för fs och då får man ett nytt önsketänkt fs'
fs'=Rms*Qts'/(2'pi*Mms)=Qts'/Qts*fs=0,38/Qts*fs=fh
Det tänkta elementet får också ett nytt Vas' som blir
Vas'=Vas*(Qts/Qts')²=Vas*(Qts/0,38 )²
och lådvolymen Vb=Vas*(Qts/0,38 )²/1,414=Vas*(Qts/0,452)²
"Svanteformlerna" för att dimensionera en nära-butterworthlösning blir alltså:
fh=fs * 0,38/Qts
Vb=Vas * (Qts/0,452)²
Man kan jämföra detta med IÖs "leksaksformler" och de andra två som man hittade på nätet:
fh=fs * 0,42/Qts
Vb=Vas/1,1 * (Qts/0,4)³
Vilket omskrivet på samma form som min formel blir
fh=fs * 0,42/Qts
Vb=Vas * (Qts/0,413)³
Formlerna är snarlika sånär som på exponenten i Vb-formeln, som är 3 i Ingvars fall och 2 i mitt.
Weedo hade dessutom lyckats spåra upp två liknande formeluppsättningar:
Vb=15*Vas*Qts^2,87
fh=fs*0,42*Qts^-0,9
Respektive
Vb=Vas * 20*Qts^3,3
fh=Fs*Vas/Vb^0,31
Skriver man om dem på samma form som mina formler så blir de:
Weedo 1:
Vb=Vas*( Qts/0,389)^2,87
fh=fs * (0,381/Qts)^0,9
Weedo 2:
Vb=Vas * (Qts/0,493)^3,3
fh=Fs*(0,493/Qts)^1,023
Puh.
Ska vi sammanställa formlerna så såg de alltså ut så här:
- Kod: Markera allt
Svante: fh=fs * 0,38/Qts Vb=Vas * (Qts/0,452)^2
IÖ: fh=fs * 0,42/Qts Vb=Vas * (Qts/0,413)^3
Weedo 1: fh=fs * (0,381/Qts)^0,9 Vb=Vas * (Qts/0,389)^2,87
Weedo 2: fh=fs * (0,493/Qts)^1,023 Vb=Vas * (Qts/0,493)^3,3
Man kan nu se vilka stora likheter det finns mellan dem. Man verkar eniga om att ungefär faktorn alfa = Qts/0,4 är viktig, liksom att fh ska vara ungefär 1/alfa ggr större än fs och att Vb ska vara alfa upphöjt till beta ggr större än Vas, där beta är mellan 2 och drygt 3.
Det här väcker lite frågor, dels varför de andra formlerna avviker från min teoretiskt välunderbyggda (hrrm) variant, dels hur formlerna har kommit till. Finns det teori bakom, eller är de helt empriska?
Finns det möjlighet att förbättra formlerna så att de ger en möjlighet till en valfri grad av underavstämning? Det är ju sällan man gör en ren butterworthlösning, numera.
Det får räcka så det blev nog långt nog...