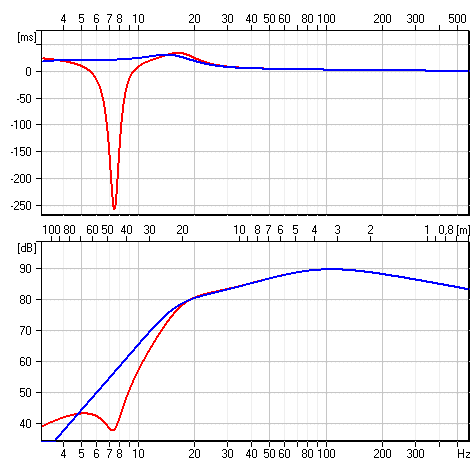
Isidor skrev:Svante skrev:Vad betyder det när grupplöptiden är negativ?
Att man har fått till en tidsmaskin, kanske?


Skämt åsido, den här frågan har stötts och blötts ganska mycket i matematikerkretsar. Ofta ser man grupplöptid, eller snarare group delay = gruppfördröjning, som ekvivalent med vad vi normalt menar med fördröjning, men detta är endast korrekt när frekvensgången är konstant.
Om frekvensgången uppträder på annat sätt måste man hantera det hela lite annorlunda. Richard Heyser har beskrivit den underliggande matematiken i ett gammalt JAES-paper: "Loudspeaker phase characteristics and time delay distortion, part 2" JAES 17 (1969) p 130-137. Kort sagt så hävdar Heyser att allpassfördröjning är "proper delay" och skriver därför om överföringsfunktionen som en konstant term och en eller flera termer av allpasstyp. Deriveringen utförs sedan termvis. På detta sätt slipper man konstigheter som negativ fördröjning och får även en mycket mer påtaglig tolkning av fördröjningsbegreppet.
Jo, jag gjorde en sökning på "negative group delay" igår och hittade en del såna där matematikerpapper. Intressant det där du säger att man delar upp överföringsfunktionen, jag antar att du menar att man gör en del som är minimumfas och en del som är allpass och som innehåller de nollställen som låg i högra s-halvplanet?
Om man sätter ihop det med min tro att ett slavbassystem
är minimumfas, så skulle det ju inte bli någon allpassdel, men det stämmer ju inte med det du säger.
Så var tror jag fel?
Annars verkar det ju som du säger att grupplöptid är ett begrepp som är väldigt lätt att tolka som fördröjning, men att den tolkningen inte riktigt håller vid en närmare analys.
Jag ska försöka hitta den där artikeln.
Så länge har jag längat efter att loudness war skulle vara över. Nu börjar jag tro att vi faktiskt är där. Kruxet är att vi förlorade.