Moderator: Redaktörer
petersteindl skrev:Det här kanske kan vara nåt att börja med? X-over
celef skrev:jag vill lära mig att bygga aktiva filter, passiva filter kan jag så att jag klarar mig
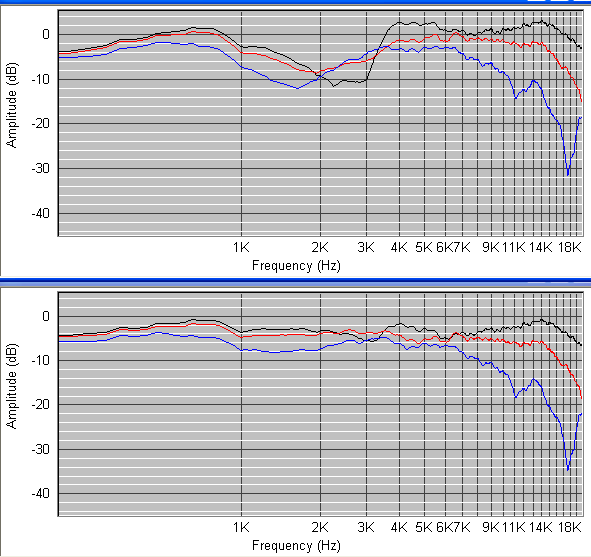
paa skrev:Det där är precis fel sätt att konstruera ett delningsfilter för en högtalare.
Det är ju de akustiska signalerna som ska delas enligt målkurvorna, inte de elektriska signalerna.
Man måste utgå från den uppmätta akustiska frekvensgången och impedansgången för respektive element för att få användbara invärden.
paa skrev:petersteindl skrev:Det här kanske kan vara nåt att börja med? X-over
Nej, det där är precis fel sätt att konstruera ett delningsfilter för en högtalare.
Det är ju de akustiska signalerna som ska delas enligt målkurvorna, inte de elektriska signalerna.
Man måste utgå från den uppmätta akustiska frekvensgången och impedansgången för respektive element för att få användbara invärden.
petersteindl skrev:En frågeställning är, hur långt ifrån blir ett optimerat resultat i jämförelse med dessa?
<snip>
Det verkor som att Svante får fixa en sån däringa kurs på KTH som han haft tidigare
Jocke skrev:Jag vill nog egentligen svag för att bygga så enkelt som möjligt...
skrutten skrev:Det vore på sin plats att med en genomgång av filter eftersom det mest bara finns beskrivningar för hur skolboksmodellen går till. Jag har i princip mest gjort samma typ av filter som kraniet men har även provat på annat. Som det första och störtsta bekymmret ser jag faktiskt möjligheten att kunna mäta själv och göra det bra. Ska man även gå in på detta?
Svante skrev:Jocke skrev:Jag vill nog egentligen svag för att bygga så enkelt som möjligt...
Finns det något skäl till det förutom att det blir enkelt?
Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Jocke skrev:Svante skrev:Jocke skrev:Jag vill nog egentligen svag för att bygga så enkelt som möjligt...
Finns det något skäl till det förutom att det blir enkelt?
Ett skäl kan ju vara att om vissa förutsättningar uppfylls kan man göra det enkelt. En annan anledning kan väl vara att komponenterna är rätt dyra - särskilt spolar. Så varför komplicera saker om det inte är nödvändigt?
adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Eri skrev:Det optimala måste väl vara det enklaste filtret som ger det resultat man vill uppnå.
Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Jocke skrev:Visst kan man sträva efter det optimala men i nästa andetag sägs det att man alltid måste kompromissa och prioritera... är det vad optimering innebär?
Det har genom åren talats en hel del om att olika topologier låter olika. Visst har olika filter olika karakteristiska egenheter men jag har en känsla av att vi bara rör oss i närheten av teorierna...
Svante skrev:Jocke skrev:Visst kan man sträva efter det optimala men i nästa andetag sägs det att man alltid måste kompromissa och prioritera... är det vad optimering innebär?
Det har genom åren talats en hel del om att olika topologier låter olika. Visst har olika filter olika karakteristiska egenheter men jag har en känsla av att vi bara rör oss i närheten av teorierna...
Ja, det där låter ju som att man måste kolla hur det är egentligen, och inte bara medelvärdesbilda vad folk säger.
Att bara välja enklaste vägen ut för att folk är oense, ptja, då optimerar man mot det man klarar att mäta (pris, arbetsinsats), en ganska typisk situation som uppstår när man optimerar med ofullständigt underlag.
Om man optimerar med en del parametrar utelämnade så är det hyfsat säkert att man inte optimerar mot de parametrarna. Så om man utelämnar ljudkvalitet och inkluderar enkelhet så är det inte troligt att högtalaren kommer att låta bra.
Nyare element med andra attraktiva egenskaper fordrar både mer avancerade filter och mer "handpåläggning".
Svante skrev:Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Varför måste det det?
Alltså, missförstå mig rätt. Man kan förstås förklara på olika sätt och de olika sätten har olika fördelar. Det finns definitivt saker som man missar om man letar upp den typiska websidan om delningsfilter i stället för att förstå matten som jag beskrev.
Eri skrev:Svante skrev:Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Varför måste det det?
Alltså, missförstå mig rätt. Man kan förstås förklara på olika sätt och de olika sätten har olika fördelar. Det finns definitivt saker som man missar om man letar upp den typiska websidan om delningsfilter i stället för att förstå matten som jag beskrev.
Måste och måste. Om det är meningen att man skall behöva ha en akademisk examen i mattematik för att hänga med här så tycker jag nivån är för hög. Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
sky_eye skrev:Eri skrev:Svante skrev:Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Varför måste det det?
Alltså, missförstå mig rätt. Man kan förstås förklara på olika sätt och de olika sätten har olika fördelar. Det finns definitivt saker som man missar om man letar upp den typiska websidan om delningsfilter i stället för att förstå matten som jag beskrev.
Måste och måste. Om det är meningen att man skall behöva ha en akademisk examen i mattematik för att hänga med här så tycker jag nivån är för hög. Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
Det finns också de som tror att man kan göra komplicerade saker enkelt.
Jocke skrev:Har kikat igenom "snutten om grundläggande delningsfilterteori" och hänger väl hyggligt med i resonemangen men som ickematematiker och ickeingenjör har jag aldrig sett formlerna uttryckas på det här sättet som jag tror är formulerad som teknisk matematik för elever med den inriktningen.
Det finns andra sätt att formulera det på så att det blir både rätt och begripligt. Så kanske vi hobbyister kan vara med i samtalet? Nog om diskussionen om diskussionen.
Hur grundläggande behöver vi vara för att någon som behöver och vill veta ska förstå?
Vi använder i huvudsak 3 olika komponenter - spolar, kondensatorer och motstånd? Hur definierar vi dem?
aisopos skrev:Och jw ger ju ingen information om fasen heller. Så det kan räcka fram till en del, men givetvis inte hela vägen.
Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Eri skrev:Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Jag tror att en duktig pedagog kan förklara även komplicerade saker så att även den mindre begåvade kan förstå. Men om man tror att det bara finns en väg mot målet så har man nog svårt att ta till sig det. Jag hade en kemilärare en gång som hade en medfödd pedagogisk talang. Han kunde beskriva dom mest komplicerade saker så att alla förstod.
Naqref skrev:aisopos skrev:Och jw ger ju ingen information om fasen heller. Så det kan räcka fram till en del, men givetvis inte hela vägen.
jw innehåller både fas- och amplitudinformation.
Almen skrev:aisopos skrev:Och jw ger ju ingen information om fasen heller.
Ja j är ju för fasen fasen!
Jocke skrev:Eri skrev:Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Jag tror att en duktig pedagog kan förklara även komplicerade saker så att även den mindre begåvade kan förstå. Men om man tror att det bara finns en väg mot målet så har man nog svårt att ta till sig det. Jag hade en kemilärare en gång som hade en medfödd pedagogisk talang. Han kunde beskriva dom mest komplicerade saker så att alla förstod.
+1
En "delningsfilterskola" för de som redan har alla sambanden klara för sig känns kanske inte så angeläget!^^
aisopos skrev:Naqref skrev:aisopos skrev:Och jw ger ju ingen information om fasen heller. Så det kan räcka fram till en del, men givetvis inte hela vägen.
jw innehåller både fas- och amplitudinformation.
Ja förlåt. Givetvis råkade det bli både fort och fel där ...
Själv har jag sedan skoltiden aldrig räknat på annat än realdelen = amplituden.
Jag får försöka skylla på det ...
KarlXII skrev:Ärligt talat blir jag jävligt trött på den skitnödiga elitism som sticker fram sitt fula ansikte här på faktiskt.se ibland.
Det går inte att förklara enkelt, det är för komplext för att förklara på ett lätt sätt, det är för många variabler = det här är för svårt för att förklara för dig, grabben, och dessutom har jag varken tid eller lust.
Man kan ju tänka sig att om en tråd har som syfte att bli en skola, så kanske någon skulle kunna tänka sig att börja på grunden. Längst ner, på det pinsamt banalt enkla.
Fast det kanske är för tråkigt?
Eri skrev:Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Jag tror att en duktig pedagog kan förklara även komplicerade saker så att även den mindre begåvade kan förstå.
Jocke skrev:KarlXII skrev:Morr!
OK - ska vi "nagelfara" skolboksfilter för att komma till ämnet?
Almen skrev:Eri skrev:Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Jag tror att en duktig pedagog kan förklara även komplicerade saker så att även den mindre begåvade kan förstå.
OK, vad är det som gör att du tror det? Jag är uppriktigt intresserad av pedagogik, eftersom jag bland annat jobbar med att försöka förklara komplicerade saker på ett enkelt sätt. Har du lust att delge lite av din erfarenhet?
KarlXII skrev:Fast det kanske är för tråkigt?
Eri skrev:Almen skrev:Eri skrev:Almen skrev:Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå.
Vad är det som gör dig övertygad om det?
Jag tror att en duktig pedagog kan förklara även komplicerade saker så att även den mindre begåvade kan förstå.
OK, vad är det som gör att du tror det? Jag är uppriktigt intresserad av pedagogik, eftersom jag bland annat jobbar med att försöka förklara komplicerade saker på ett enkelt sätt. Har du lust att delge lite av din erfarenhet?
Bäste herr Almen. Den här diskussionen hör inte hemma i den här tråden. Jag är själv inte pedagog. Jag talar om min erfarenhet som elev. Vissa människor har förmågan att på ett enkelt sätt förklara svåra saker andra krånglar bara till det hela. Om du har problem att förklara saker för andra ska du kanske låta någon annan göra det i stället. Så får du gärna ta med hela citatet. Nu anser jag den här diskussionen eller vad man skall kalla det avslutad.
Almen skrev:Ja, det var ju du som inledde med att kritisera Svante, som om han vore ett exempel på en dålig pedagog. Men visst, diskussionen blev inte så fruktbar, det har du rätt i.
Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Jocke skrev:Fattar inte alls varför det känns som du hackar på mig...
KarlXII skrev:Almen skrev:Ja, det var ju du som inledde med att kritisera Svante, som om han vore ett exempel på en dålig pedagog. Men visst, diskussionen blev inte så fruktbar, det har du rätt i.
Kritisera? Dålig pedagog?adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Var såg du det sa du?
Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
Almen skrev:KarlXII skrev:Almen skrev:Ja, det var ju du som inledde med att kritisera Svante, som om han vore ett exempel på en dålig pedagog. Men visst, diskussionen blev inte så fruktbar, det har du rätt i.
Kritisera? Dålig pedagog?adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Var såg du det sa du?Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
petersteindl skrev:Ett simuleringsprogram som jag tycker är enkelt och bra är Svantes Basta.
Svante skrev:Jocke skrev:Fattar inte alls varför det känns som du hackar på mig...
Nej, förlåt, jag var nog lite för brutalraktpåsak.
Beräkningarna blir mycket kortare med jw-metoden, men förutsätter att man behärskar komplexa tal. Exemplet ovan är valt som ganska enkelt i det att amplituderna är lika och fasvinkeln är komfortabla 90 grader. Verkliga exempel blir snabbt ohanterbara med vanliga sinusar och man får nöja sig med resonemang.
Problemet med jw-metoden är att man måste behärska komplexa tal.
...och så är det bara. Resonemang kring sinusar är en återvändsgränd. De funkar för övergripande resonemang, men söker man djupare förklaringar så funkar inte det med sinusarna.
Eri skrev:Almen skrev:KarlXII skrev:Almen skrev:Ja, det var ju du som inledde med att kritisera Svante, som om han vore ett exempel på en dålig pedagog. Men visst, diskussionen blev inte så fruktbar, det har du rätt i.
Kritisera? Dålig pedagog?adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Var såg du det sa du?Eri skrev:Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
Jag förstår inte var du fick det ifrån att detta var riktat till Svante. Det var överhuvudtaget inte riktat till någon speciell person.
PappaBas skrev:Detta är en jättebra grundläggande förklaringar som man använda på vanlig gymnasiematte.
http://www.pispeakers.com/Speaker_Crossover_Lab.pdf
Denna förklarar också väldigt bra vad det hela går ut på:
http://www.ti.com/lit/an/snoa224a/snoa224a.pdf
Almen skrev:Varför skrev du det som svar till Svante, då? Varför skriva det alls?
Eri skrev:Det var inget svar till Svante. Finns det ingen här på forumet som kan få stopp på Almen. Jag börjar bli djävligt trött på honom nu. Nu får fan i mig den här diskussionen vara avslutad.
PappaBas skrev:Detta är en jättebra grundläggande förklaringar som man använda på vanlig gymnasiematte.
http://www.pispeakers.com/Speaker_Crossover_Lab.pdf
PappaBas skrev:Denna förklarar också väldigt bra vad det hela går ut på:
http://www.ti.com/lit/an/snoa224a/snoa224a.pdf
celef skrev:Alexi skrev:Om vi först kanske kunde definiera målen med ett delningsfilter
+1, på molekylnivå

Jocke skrev:Det börjar arta sig!
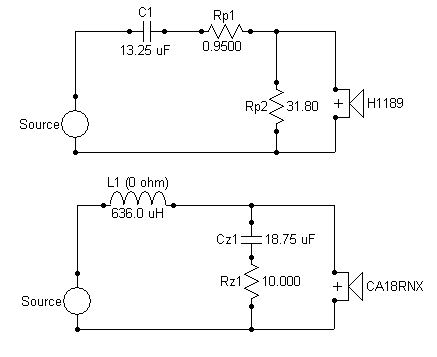
Upptäckte ett, för mig, nytt och annorlunda sätt att göra notch-filter hos Troels för en tid sedan. (Efter tips från en forummedlem).
Någon som kan förklara?
(Det gäller alltså konding och motstånd i serie över spolen för ER18RNX)
Eri skrev:Svante skrev:Eri skrev:adzer skrev:Svante skrev:Jag skrev ihop en snutt om grundläggande delningsfilterteori för ganska länge sedan.
http://user.faktiskt.io/delningsfilter.htm
Denna länk funkar bättre:
http://user.faktiskt.io/svante/delningsfilter.htm
Det där verkar alldeles för avancerat. Det måste ju gå att förklara hur delningsfilter fungerar på ett enkelt och lättfattligt sätt.
Varför måste det det?
Alltså, missförstå mig rätt. Man kan förstås förklara på olika sätt och de olika sätten har olika fördelar. Det finns definitivt saker som man missar om man letar upp den typiska websidan om delningsfilter i stället för att förstå matten som jag beskrev.
Måste och måste. Om det är meningen att man skall behöva ha en akademisk examen i mattematik för att hänga med här så tycker jag nivån är för hög. Jag är övertygad om att det går om man bara vill att förklara även komplicerade saker på ett enklare sätt så att alla kan förstå. Men alla kanske inte har den förmågan. Det finns ju personer som alltid skall göra saker svårare än vad som är nödvändigt.
IngOehman skrev:Så om du bara substituerar s med jw så bli det mycket enklare,
i varje fall om du även vet att w är s*pi*f.
Vh, iö
Svante skrev:Spole och kondensator i parallell får en admittans som blir summan av kondensatorns och spolens admittanser. 1/Zc+ 1/Zl = jwC+1/jwL=jwC-j/wL=j(wC-1/wL).
Det är alltså en rent imaginär admittans (ström och spänning ligger 90 grader ur fas) som dessutom är noll när wC=1/wL eller w=1/sqrt(LC). Vid en frekvens leder den inte alls.
Efter lite fnulande med jw-metoden (hinner inte nu) kommer man fram till att resistorerna gör att det ändå blir en viss ledningsförmåga vid resonansfrekvensen, notchens djup beror alltså av resistanserna. Vid höga frekvenser verkar kretsen som kondensatorns serieresistans, vid låga frekvenser som spolens serieresistans.
IngOehman skrev:...
Exempelvis tror jag (som bara skummade igenom det han skrev) att han
skippar definitionen på s (som är den frekvensberoende reaktiva kompo-
nenten). Så om du bara substituerar s med jw så bli det mycket enklare,
i varje fall om du även vet att w är s*pi*f.
Vh, iö
Morello skrev:Tror man ska vara lite försiktig med att introducera laplaceoperatorn utan att förklara var den kommer från, men det är utanför ramen för tråden då det tarvar mycket mer matematik än vad som predikas på gymnasienivå.
Ingvar skriver ang. s "som är den frekvensberoende reaktiva kompo-
nenten", vilket är direkt fel.
s är komplex, dvs s=sigma+jw
Almen skrev:Morello skrev:Tror man ska vara lite försiktig med att introducera laplaceoperatorn utan att förklara var den kommer från, men det är utanför ramen för tråden då det tarvar mycket mer matematik än vad som predikas på gymnasienivå.
Ingvar skriver ang. s "som är den frekvensberoende reaktiva kompo-
nenten", vilket är direkt fel.
s är komplex, dvs s=sigma+jw
Men i fallet Laplace/Fourier substituerar man ju s med jw, alltså s=jw=j2πf.

Nattlorden skrev:Väldigt åskådliggörande animation, Peter!
petersteindl skrev:Nattlorden skrev:Väldigt åskådliggörande animation, Peter!
Ja, jag gillar den jättemycket. Bra animationer is da shit. Därför tror jag på läsplattor inför framtidens undervisning.
Morello skrev:Tror man ska vara lite försiktig med att introducera laplaceoperatorn utan att förklara var den kommer från, men det är utanför ramen för tråden då det tarvar mycket mer matematik än vad som predikas på gymnasienivå.
Ingvar skriver ang. s "som är den frekvensberoende reaktiva kompo-
nenten", vilket är direkt fel.
s är komplex, dvs s=sigma+jw
Morello skrev:Almen skrev:Morello skrev:Tror man ska vara lite försiktig med att introducera laplaceoperatorn utan att förklara var den kommer från, men det är utanför ramen för tråden då det tarvar mycket mer matematik än vad som predikas på gymnasienivå.
Ingvar skriver ang. s "som är den frekvensberoende reaktiva kompo-
nenten", vilket är direkt fel.
s är komplex, dvs s=sigma+jw
Men i fallet Laplace/Fourier substituerar man ju s med jw, alltså s=jw=j2πf.
Det gör man om man vill undersöka hur en funktion H(s) beter sig för stationära signaler - ja, men det är långt från hela sanningen.
Svante skrev:Morello skrev:Tror man ska vara lite försiktig med att introducera laplaceoperatorn utan att förklara var den kommer från, men det är utanför ramen för tråden då det tarvar mycket mer matematik än vad som predikas på gymnasienivå.
Ingvar skriver ang. s "som är den frekvensberoende reaktiva kompo-
nenten", vilket är direkt fel.
s är komplex, dvs s=sigma+jw
Ja, jag brukar använda s i stället för jw för att man blir så less på att skriva jw, och att man får en massa minustecken som det alltid blir fel med.
Svante skrev:Det är alltså en rent imaginär admittans (ström och spänning ligger 90 grader ur fas) som dessutom är noll när wC=1/wL eller w=1/sqrt(LC). Vid en frekvens leder den inte alls.
Efter lite fnulande med jw-metoden (hinner inte nu) kommer man fram till att resistorerna gör att det ändå blir en viss ledningsförmåga vid resonansfrekvensen, notchens djup beror alltså av resistanserna. Vid höga frekvenser verkar kretsen som kondensatorns serieresistans, vid låga frekvenser som spolens serieresistans.
Jocke skrev:Tyst ett tag redan... tröttnat?^^
Nattlorden skrev:Tror inte de flesta vill begrunda filter riktigt så här teoretiskt. I alla fall inte som start...
Svante skrev:Z=1/ ( 1/(Rl+jwl) + 1/(Rc+1/jwC) )= ... =(Rl+jwL)(1+jwRcC)/(1+jwC(Rc+Rl)-w²LC)
Typ.
Morello skrev:Jag kan garantera att man måste börja med teoretiska studier för att lära sig denna konst. Det är väl bara att insupa den hjälp som tex. Svate och Ingvar erbjuder?
Studier, praktik, mer studier och mer experiment och till slut kan man njuta av arbetets frukter.Är det inte det som är rätt så skoj - att lära sig nya saker?
Nattlorden skrev:Tror inte de flesta vill begrunda filter riktigt så här teoretiskt. I alla fall inte som start...
KarlXII skrev:Morello skrev:Jag kan garantera att man måste börja med teoretiska studier för att lära sig denna konst. Det är väl bara att insupa den hjälp som tex. Svate och Ingvar erbjuder?
Studier, praktik, mer studier och mer experiment och till slut kan man njuta av arbetets frukter.Är det inte det som är rätt så skoj - att lära sig nya saker?
Både ja och nej.
Det är inte meningsfullt att lära sig INS-navigation när man inte ens vet varför planet flyger. Eller vad man ska ha ett flygplan till.
Grunderna först, kan det vara något?
KarlXII skrev:Grunderna först, kan det vara något?
Fjonkalicious skrev:Vissa här basunerar ut att man minsann måste kunna det teoretiska sambandet av en koppling, annars kan man ju inte köra bil. När någon då säger att det faktiskt går så blir svaret att man inte kan köra bil bra utan att det är ett förenklat sätt att se på saker.
Fjonkalicious skrev:Se det som teori och praktik i bilkörning. Du kan inte vara i trafiken utan teori och du kan inte köra bil utan praktik( nu är der ju säkerligen någon här som kunde köra bil när dom var 12 genom att bara ha läst teori och praktisera det själv, men snälla lämna den diskussionen).
kraniet skrev:en tråd med samlad kunskap om delningsfilter
Almen skrev:Men vad bra, Peter S och Svante borta.
Hade man inte kunnat ha lite mer tillåtande atmosfär, i enlighet med TS första inlägg [min fetning]:kraniet skrev:en tråd med samlad kunskap om delningsfilter
Men det skall tydligen godkännas av faktiskts anti-intellektualism-maffia först. Ingen får skriva något som jag inte förstår omedelbart! Skitnödig elitism!
Skulle det inte kunna finnas plats för både teoretiska och praktiska resonemang?
Fjonkalicious skrev:Almen skrev:Men vad bra, Peter S och Svante borta.
Hade man inte kunnat ha lite mer tillåtande atmosfär, i enlighet med TS första inlägg [min fetning]:kraniet skrev:en tråd med samlad kunskap om delningsfilter
Men det skall tydligen godkännas av faktiskts anti-intellektualism-maffia först. Ingen får skriva något som jag inte förstår omedelbart! Skitnödig elitism!
Skulle det inte kunna finnas plats för både teoretiska och praktiska resonemang?
Du kom ju verkligen långt att hjälpa till trådens syfte med att konstant hacka på Eri. Bra jobbat!
Fjonkalicious skrev:Jag kommenterar inte metadebatten för det förlänger den bara.
Men jag läste igenom tråden och försökte hitta något annat som verkade bidragande från din sida och såg bara någon enstaka formel men inget annat matnyttigt. Vad är ditt syfte med ditt deltagande i tråden?
Fjonkalicious skrev:Det låter som ett litet skevt sätt att se på hantverk tycker jag. Upplever inte att man gör utan att förstå varför.
Hur många här lärde sig att köra bil genom att först förstå fordonets exakt alla delar och funktioner? Visst, det hade nog förenklat för många för att man kunde påvisa vad som faktiskt händer när du släpper på pedalens till vänster...
carpelux skrev:Jag har ett konstruktivt förslag, det är ju onekligen ett komplext ämne med stor spännvidd så varför inte skapa 2 trådar, "Faktiskt.se delningsfilterskola grundkurs" och "Faktiskt.se delningsfilterskola - avancerat".
Dessa skulle ju kunna existera parallellt.
Naqref skrev:
Vad jag vill säga är att man klarar faktiskt sig med vissa av kunskaperna.
KarlXII skrev:Nattlorden skrev:Tror inte de flesta vill begrunda filter riktigt så här teoretiskt. I alla fall inte som start...Svante skrev:Z=1/ ( 1/(Rl+jwl) + 1/(Rc+1/jwC) )= ... =(Rl+jwL)(1+jwRcC)/(1+jwC(Rc+Rl)-w²LC)
Typ.
Där fick du allt svar på tal, Nattis!
Fjonkalicious skrev:...
Alla lämnar, varför? Är man för lättstött?
Mvh
Morello skrev:Jag kan garantera att man måste börja med teoretiska studier för att lära sig denna konst. Det är väl bara att insupa den hjälp som tex. Svante och Ingvar erbjuder?
Studier, praktik, mer studier och mer experiment och till slut kan man njuta av arbetets frukter.Är det inte det som är rätt så skoj - att lära sig nya saker?
carpelux skrev:Jag har ett konstruktivt förslag, det är ju onekligen ett komplext ämne med stor spännvidd så varför inte skapa 2 trådar, "Faktiskt.se delningsfilterskola grundkurs" och "Faktiskt.se delningsfilterskola - avancerat".
Dessa skulle ju kunna existera parallellt.
Kraniet skrev:Det vore väl skoj om vi kunde få igång en tråd med samlad kunskap om delningsfilter. Vilken typ, ordning och målkurva etc. Hantering av peaks, optimisering för off-axis osv.
Kanske inte så mycket vad som är "bäst" utan mera prat om vilka konsekvenser vissa lösningar får, för vilka ändamål de är meningsfulla osv. Även tillvägagångssätt vid dimensionering och optimering av högtalare kan ju vara intressant.
Någon som nappar på det?
Svante skrev:
Då kan vi först käbbla om vilken som ska vara vilken...
(Grundkursen är rimligen den med ellära, jw-metoden och laplacetransformen, den avancerade är hur man applicerar grundkursen på verkligheten. Eller)
petersteindl skrev:Jag lämnade diskussionen eftersom jag fick intrycket att mina inlägg inte behövdes. Det var inte så mycket feedback från de som började skriva i tråden d v s från de som tyckte ämnet var bra och ville ha mer info.
...
Mvh
Peter
Svante skrev:
Nudå.
...
Som en vanlig resonanskrets mao. Polerna ("nollställena i nämnaren") motsvarar ju resonanser om man släpper systemet fritt, och om man frikopplar kretesn från allt omgivande så blir den ju de fyra komponenterna i serie i en slinga. Släpper man den fri kommer det att ringa med resonansfrekvensen w0=1/sqrt(LC) och med ett Q-värde som motsvaras av de två resistanserna i serie med L och C.
Typ.
carpelux skrev: Själv tror jag att den avancerade matten effektivt utesluter en stor del av de intresserade. Lika effektivt som om inläggen varit skrivna på ryska. De flesta kan givetvis lära sig hantera både den avancerade matten eller ryska men tröskeln för det är så hög att man helt enkelt avstår.





phon skrev:carpelux skrev: Själv tror jag att den avancerade matten effektivt utesluter en stor del av de intresserade. Lika effektivt som om inläggen varit skrivna på ryska. De flesta kan givetvis lära sig hantera både den avancerade matten eller ryska men tröskeln för det är så hög att man helt enkelt avstår.
Det är bra att min mattebok är skriven på ryska då, två flugor på samma smäll liksom ....
---
Kapitlet om fastransformation i elastiska sfärer är intressant för förståelsen av dome-membrans uppförande och kontroll. Det måste väl nästan vara med i grundkursen.
Almen skrev: ...Scanna in och lägg som första inlägg i grundkurs-tråden.


carpelux skrev:Svante skrev:
Då kan vi först käbbla om vilken som ska vara vilken...
(Grundkursen är rimligen den med ellära, jw-metoden och laplacetransformen, den avancerade är hur man applicerar grundkursen på verkligheten. Eller)
Ja så kan man ju välja att se på saken.
Själv tror jag att den avancerade matten effektivt utesluter en stor del av de intresserade. Lika effektivt som om inläggen varit skrivna på ryska. De flesta kan givetvis lära sig hantera både den avancerade matten eller ryska men tröskeln för det är så hög att man helt enkelt avstår.
Om det är så att det är ett absolut krav att kunna räkna med komplexa tal för att kunna ha någon förståelse för hur ett delningsfilter fungerar och är dimensionerat, ja då är det väl bara att inse att man är "out". Då blir det ju i stort sett endast de redan invigda kvar, och frågan är om det är de som behöver en skola?
Svante skrev:(Grundkursen är rimligen den med ellära, jw-metoden och laplacetransformen, den avancerade är hur man applicerar grundkursen på verkligheten. Eller)
Jag tror att dom bara kör i två dimensioner, dom där sabla operatorerna är alldeles för kraftfulla.petersteindl skrev:@ fån:Men jag ser ju inga nablaoperatorer
å vars är alla tensorer?
Hur skall man då få lekmän att förstå de trivialt enkla sambanden?
Mvh
Peter
Almen skrev:Men vad bra, Peter S och Svante borta.
Hade man inte kunnat ha lite mer tillåtande atmosfär, i enlighet med TS första inlägg [min fetning]:kraniet skrev:en tråd med samlad kunskap om delningsfilter
Men det skall tydligen godkännas av faktiskts anti-intellektualism-maffia först. Ingen får skriva något som jag inte förstår omedelbart! Skitnödig elitism!
Skulle det inte kunna finnas plats för både teoretiska och praktiska resonemang?
phon skrev:Jag gjorde ett nytt filter till en OA-högtalare idag. Häromdagen tänkte jag igenom dimensioneringen och idag utförde jag det hela praktiskt. Inte en siffra är räknad på det filtret, inte småskolematte ens. Det är nog ytterst sällan jag räknar på något filter.
Jag kommer ihåg att jag räknade på filter på 70-talet, och det fungerade rätt bra det också. Numera slickar jag på fingret och håller upp det i luften för att känna vartåt det blåser. Sedan tittar jag i skrotlådan vilka komponenter jag har ... och så blir det ett helt perfekt filter efter en stund.
Ibland en ganska lång stund förvisso, det kan ta sina dagar och veckor. Det ligger liksom och mognar nånstans i bakhuvudet, men så helt plötsligt poppar det upp en lösning som jag kan prova. Det är ju inte bara filtren som ligger och ruvar där i bakhuvudet, det är element och bafflar, lådor och avstämningar, allt verkar hänga ihop på nåt mystiskt sätt.
Tur att jag slipper räkna på sånt, då skulle jag inte hinna bygga några högtalare ...
carpelux skrev:Svante skrev:
Då kan vi först käbbla om vilken som ska vara vilken...
(Grundkursen är rimligen den med ellära, jw-metoden och laplacetransformen, den avancerade är hur man applicerar grundkursen på verkligheten. Eller)
Ja så kan man ju välja att se på saken.
Själv tror jag att den avancerade matten effektivt utesluter en stor del av de intresserade. Lika effektivt som om inläggen varit skrivna på ryska. De flesta kan givetvis lära sig hantera både den avancerade matten eller ryska men tröskeln för det är så hög att man helt enkelt avstår.
Svante skrev:Annars så verkar det väl trevligt att man, givet att man har koll på hur elektriska kretsar fungerar, diskuterar hur man hanterar tex högtalarelementens impedanser och hur de får filtren att bete sig på ett sätt som inte liknar kokboksfiltret. Hur baffelsteget hanteras i filtret, etc.
----
-----| |--------+----------
---- |
R1 |
-
| |
U1 R2 | | U0
| |
-
|
|
-------------------+---------- ----
-----| |--------+----------
---- |
R |
|
-------
U1 C U0
-------
|
|
|
|
-------------------+---------- Svante skrev:carpelux skrev:Svante skrev:
Då kan vi först käbbla om vilken som ska vara vilken...
(Grundkursen är rimligen den med ellära, jw-metoden och laplacetransformen, den avancerade är hur man applicerar grundkursen på verkligheten. Eller)
Ja så kan man ju välja att se på saken.
Själv tror jag att den avancerade matten effektivt utesluter en stor del av de intresserade. Lika effektivt som om inläggen varit skrivna på ryska. De flesta kan givetvis lära sig hantera både den avancerade matten eller ryska men tröskeln för det är så hög att man helt enkelt avstår.
Ja, jag förstår att det är det som händer, och vad jag försöker att säga är att det är MINDRE jobb att lära sig den där matten än att sitta i timtal och nästanförstå hur filtren kanske funkar med sinusar som spelar halvt i fas osv.
Jag ska berätta en anekdot om hur det gick till när jag lärde mig jw-metoden. Det var när jag gick i gymnasiet, jag satt ofta på kvällarna och funderade på hur filter fungerade och hade just kommit till insikt om hur ett första ordningen filter fungerade. Med hjälp av vektorer som representerade fasförskjutna sinusar hade jag äntligen förstått hur det kunde bli 0,7 volt både över kondingen och motståndet, trots att de matades med totalt 1 V.
Jag berättade det för min fysiklärare, och då sade han att jag borde räkna med jw-metoden i stället. Jag hade sett namnet i någon "Radio och Television" men inte fattat hur imaginära tal skulle kunna tillföra något verkligt. Jag frågade hur det fungerade, och han sade att kondensatorers och spolars impedanser kan ses som imaginära och resistanser kunde ses som reella.
Det sade klick direkt, och därefter bara smålog jag över mina tidigare försök med vektorer. Det är de försöken jag ser upprepas i många diskussioner om filter.
Så, nu vet ni det. Om nu någon undrade.
Annars så verkar det väl trevligt att man, givet att man har koll på hur elektriska kretsar fungerar, diskuterar hur man hanterar tex högtalarelementens impedanser och hur de får filtren att bete sig på ett sätt som inte liknar kokboksfiltret. Hur baffelsteget hanteras i filtret, etc.
IngOehman skrev:Men riktigt spännande blir det ju inte förrän två sakers summa
blir mindre än någon av dem som enskildhet...
IngOehman skrev:Å andra sidan så kan man ju fråga som om inte jw-metoden är just
vektoraddition... Det är lätt att se hur ekvationerna sammanfaller.
PappaBas skrev:Almen skrev:Skulle det inte kunna finnas plats för både teoretiska och praktiska resonemang?
För att förstå tror jag man måste ha en iterativ process där man arbetar med teori och praktik om vartannat.
IngOehman skrev:Jag förstår hur du tänker, men jag är inte alldeles säker på att det är en
fördel, alltså för intuitionens utvecklande att "slippa fundera på vektor-
erna och deras vinklar medan man räknar".
Tycker nog att man bollar noggrannast när man har hela bilden framför
sig, hela tiden.
IngOehman skrev:Vad jag menade med en summa som blir mindre än enskildheterna var
att man om man summerar impedansen från en kondensator och en spole,
påsäg 10 uF och 1 mH, vid höga frekvenser för en impedans som unge-
färligen stämmer med spolen och vid låga får en som ungefärligen stäm-
mer med kondensatorns - med mittemellan så blir det noll.
IngOehman skrev:Över en timme faktiskt. Men att på det här viset pladdra fram sina egna
tankar är ju ändå väldigt mycket lättare än att fundera på något (och sen
skriva om det) som man inte sett klart för sig utan och innan i över 40 år.
En intressant sak jag märkt är dock att sådan här saker oftast är väldigt
mycket enklare att förmedla live, på föreläsningar med tillgång till en tavla
att rita på.
Många kommer lätt av sig, har jag märkt, när de behöver båda tänka och
läsa. Det är kanske lättare att tänka och lyssna? Då kan man liksom låna
någon annans initiativ som motor. Inte vet jag. Men jag har många gånger
stött på att folk som jag vet läst sådant jag skrivit, ändå inte förstår förr-
än man berättar samma sak "live". Så kanske är föreläsningsformen, i varje
fall för vissa, ändå att föredra?
Vh, iö
PappaBas skrev:Kanske dålig liknelse, men förenklat tänker jag mig det som varje frekvenskomponent kan tänkas som en liten kul som släpps ner längs duken längs frekvensaxeln.
Lutningar, dalar och toppar kommer att påverka tiden det tar för den att nå sitt mål på andra sidan. Lite som det där träspelet man hade med en kula när man var barn med två vred på sidan och man skulle navigera så det inte föll ner i hål?
Får kanske göra en lex maria på mig själv till liknelsepolisen...
IngOehman skrev:Fast liknelsen halter lite på så vis att endast snittet längs s-(eller jw-)axeln,
Vh, iö
Svante skrev:Ska vi berätta vad talet j är också, för den som inte vet?
Det är ett märkligt tal, som på sätt och vis inte finns. Fast det är som vi har sett ganska trevligt att använda ändå.
Det börjar med att man vill ta roten ur tal. Man frågar sig "Vilket tal gånger sig själv blir det här?". Så roten ur 4 är 2 eftersom 2*2=4, roten ur 9 är 3 eftersom 3*3=9, roten ur 100 är 10. Och roten ur 1 är 1
Men var är roten ur -1? Det är inte -1 eftersom (-1)*(-1)=1. Med vanlig matte (med reella tal) så går det inte att ta roten ur -1. För att ändå kunna räkna vidare definierar man ett tal j som är roten ur -1, trots att det inte finns. Det får den märkliga egenskapen att j²=-1, i övrigt kan man räkna med det som vilken konstant som helst.
...och när man gör så öppnar sig en helt ny värld inom matematiken, och en av frukterna är jw-metoden. Talet j löser en hel del problem i matematiken som knappast skulle gå att behandla annars, tex linjära differentialekvationer med sinuslösningar, tex sådana som blir när en sträng klingar av. Pling!
IngOehman skrev:Fast det är väl bara elektronik/hifi/fysik-tokar som säger j?
Riktiga matematiker säger väl i, eller?
^^^
------ --------+------+---------
L | |
| |
| -
------- | |
U1 C | | R Ul
------- | |
| -
| |
| |
| |
-----------------+------+---------
| |
-------| |---------+----+---------
| | | |
C | -
) | |
U1 L ) | | R Uh
) | |
| -
| |
| |
-------------------+----+---------
Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Svante skrev:IngOehman skrev:Fast det är väl bara elektronik/hifi/fysik-tokar som säger j?
Riktiga matematiker säger väl i, eller?
Riktiga matematiker vet att båda konventionerna finns och kan använda båda. Har de nått över en viss nivå så bryr de sig märkligt lite om konventioner (som bokstavsval) är min erfarenhet.
Svante skrev:Och det finns ett s-plan (Laplaceplanet), med en jw-axel (ordinatan, "y-axeln"). Om man studerar delmängden av s-planet som är jw-axeln så kan man bla se tonkurvan. Alltså, har man räknat med laplacetransform och har ett uttryck med s i, så kan man byta s mot jw, ta beloppet och få tonkurvan.
IngOehman skrev:Visst, snittet i planet, längs imaginära (jw)axeln.
Vh, iö
IngOehman skrev:Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Fast nu vete tusan om det inte finns risk att någon blir vilseledd ändå.
Tänker på det där med "typiskt fasvänder".
Vete tusan hur typiskt det är.
Det är inte ovanligt med delningsfrekvenser om 3000 Hz (λ/2=5,7 cm) och
det är inte helt osannolikt att skillnaden i akustiskt avstånd till respektive
element är i den storleksordningen. Inte heller är det ovanligt att samman-
lagda fasvridningen från de två elementens egna överföringsfunktioner, läs
skillnaden mellan dem vid lyssningsplats, är signifikant.
I läroböcker tillhör det vanligheten att man får veta att diskantelementet
skall fasvändas när andra ordningens filter används, men i praktiken vill jag
nog påstå att det är troligare, eller i varje fall lika troligt, att en icke-fas-
vänd inkoppling kommer att summera bättre.
Dock skall man inte utesluta att en fasvänd inkoppling är rätt och att det
kan bero på att de nämnda faktorerna har adderat ett helt varv!
Vh, iö
Jocke skrev:Hmmm... Så vad är det som har åstadkommitrs på alla dessa sidor nu då? En ny definition på "skolboksfilter"???
IngOehman skrev:Fast det är väl bara elektronik/hifi/fysik-tokar som säger j?
Riktiga matematiker säger väl i, eller?
IngOehman skrev:Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Fast nu vete tusan om det inte finns risk att någon blir vilseledd ändå.
Tänker på det där med "typiskt fasvänder".
IngOehman skrev:Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Fast nu vete tusan om det inte finns risk att någon blir vilseledd ändå.
Tänker på det där med "typiskt fasvänder".
Vete tusan hur typiskt det är.
Det är inte ovanligt med delningsfrekvenser om 3000 Hz (λ/2=5,7 cm) och
det är inte helt osannolikt att skillnaden i akustiskt avstånd till respektive
element är i den storleksordningen. Inte heller är det ovanligt att samman-
lagda fasvridningen från de två elementens egna överföringsfunktioner, läs
skillnaden mellan dem vid lyssningsplats, är signifikant.
chrisss skrev:Jocke skrev:Hmmm... Så vad är det som har åstadkommitrs på alla dessa sidor nu då? En ny definition på "skolboksfilter"???
Det har än en gång bevisats att enbart teoretiska kunskaper
Inte räcker för att lösa verkliga problem.
Jag är tämligen säker på att Kraniet redan visste det när han
startade tråden.
En högtalare är komplex!
Man skulle kunna vara doktor i filterteori men ändå inte klara av
att konstruera en god högtalare.
aisopos skrev:IngOehman skrev:Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Fast nu vete tusan om det inte finns risk att någon blir vilseledd ändå.
Tänker på det där med "typiskt fasvänder".
Vete tusan hur typiskt det är.
Det är inte ovanligt med delningsfrekvenser om 3000 Hz (λ/2=5,7 cm) och
det är inte helt osannolikt att skillnaden i akustiskt avstånd till respektive
element är i den storleksordningen. Inte heller är det ovanligt att samman-
lagda fasvridningen från de två elementens egna överföringsfunktioner, läs
skillnaden mellan dem vid lyssningsplats, är signifikant.
Och om jag inte har missuppfattat saker och ting nu, så beror det väl på vilken filterfunktion man väljer
(Butterworth, bessel, Chebyshev, osv) hur mycket fasskillnaden mellan diskant och bas blir?
UrSv skrev:celef skrev:bra tråd! verkligen!
varför står det så här så fort svante skriver något?Senast ändrad av Svante den lör okt 20, 2012 9:24 pm, ändrad totalt 1 gång.
För att Svante skriver inlägget, postar och sen filar lite till på det.
jonasp skrev:UrSv skrev:celef skrev:bra tråd! verkligen!
varför står det så här så fort svante skriver något?Senast ändrad av Svante den lör okt 20, 2012 9:24 pm, ändrad totalt 1 gång.
För att Svante skriver inlägget, postar och sen filar lite till på det.
Nej, för att något är bananas på faktiskt.se i databaaauusen eller så!
Nattlorden skrev:IngOehman skrev:Fast det är väl bara elektronik/hifi/fysik-tokar som säger j?
Riktiga matematiker säger väl i, eller?
Ja. Men som Svante påpekar så förstår vi substitutionen, även om det skär i kroppen på varje j...
Svante skrev:IngOehman skrev:Svante skrev:Detta är orsaken till att man typiskt fasvänder diskanten i ett andra ordningens delningsfilter.
Fast nu vete tusan om det inte finns risk att någon blir vilseledd ändå.
Tänker på det där med "typiskt fasvänder".
Njaej, alltså, bara så det är fullständigt klart: Jag pratar om det teoretiska fallet med kokboksfilter, med resistiv last, utan högtalarelemet och akustiska avstånd. I sådana resonemang fasvänder man typiskt det diskantelement (som inte finns).
Svante skrev:jonasp skrev:UrSv skrev:celef skrev:bra tråd! verkligen!
varför står det så här så fort svante skriver något?Senast ändrad av Svante den lör okt 20, 2012 9:24 pm, ändrad totalt 1 gång.
För att Svante skriver inlägget, postar och sen filar lite till på det.
Nej, för att något är bananas på faktiskt.se i databaaauusen eller så!
Hehe, nej admin behöver inte felsöka databasen...
Svante skrev:Jag anar fortfarande viljan att få snabba lättfattliga fixar för att uppnå det perfekta resultatet. Då ska man inte läsa det jag skriver.
IngOehman skrev:Svante skrev:Jag anar fortfarande viljan att få snabba lättfattliga fixar för att uppnå det perfekta resultatet. Då ska man inte läsa det jag skriver.
Äntligen har du konverterat till en rekorderlig tumregelmotståndare!
Vh, iö
Nattlorden skrev:IngOehman skrev:Fast det är väl bara elektronik/hifi/fysik-tokar som säger j?
Riktiga matematiker säger väl i, eller?
Ja. Men som Svante påpekar så förstår vi substitutionen, även om det skär i kroppen på varje j...
IngOehman skrev:Svante skrev:Jag anar fortfarande viljan att få snabba lättfattliga fixar för att uppnå det perfekta resultatet. Då ska man inte läsa det jag skriver.
Äntligen har du konverterat till en rekorderlig tumregelmotståndare!
Vh, iö
Svante skrev:IngOehman skrev:Svante skrev:Jag anar fortfarande viljan att få snabba lättfattliga fixar för att uppnå det perfekta resultatet. Då ska man inte läsa det jag skriver.
Äntligen har du konverterat till en rekorderlig tumregelmotståndare!
Vh, iö
Inte alls.
Morello skrev:IngOehman skrev:Svante skrev:Jag anar fortfarande viljan att få snabba lättfattliga fixar för att uppnå det perfekta resultatet. Då ska man inte läsa det jag skriver.
Äntligen har du konverterat till en rekorderlig tumregelmotståndare!
Vh, iö
Mja, jag tror aldrig Svante har förespråkat genvägar, utan snarare predikat riktig kunskap.
IngOehman skrev:Ja, så kan det förstås vara. Men vad han än kallar förenklingarna är jag glad
att han övergivit sin entusiasm för dem, till förmån för att varna för tron på
att snabba lättfattliga fixar duger för att uppnå det perfekta resultatet.
Det var på tiden.
IngOehman skrev:Jag föreställer mig att de som gillar aktiva filter är av uppfattningen att
det är just att dela signalen i två halvor (som passar respektive högtalar-
element) som är filtrets uppgift.
Men jag, som i de flesta applikationer ser stora, stora fördelar fångbara
med hjälp av passiva filter, är av en väldigt annorlunda uppfattning. Det
finns dock fall när aktiva filter är bäst. Klart bäst till och med.
Det beror på, och det beror på en väldig massa olika saker.
Vh, iö
IngOehman skrev:Ja, så kan det förstås vara. Men vad han än kallar förenklingarna är jag glad
att han övergivit sin entusiasm för dem, till förmån för att varna för tron på
att snabba lättfattliga fixar duger för att uppnå det perfekta resultatet.
Det var på tiden.
PappaBas skrev:Det jag skulle vilja veta mer om är hur man får fasen att bete sig som man vill? Vet ju att det finns allpassfilter osv men använder man dem i högtalarfilter?
I ett datorprogram kan man ju med ren beräkningskraft optimera tonkurva, impedans och fas. Men det vore kul att förstå mer och inte bara ansätta ett filter med målkurvor och låta datorn göra jobbet som jag gör (har ju egentligen ingen koll om det är en lämplig ansats ens).
Hur gör ni proffs?
petersteindl skrev:
Ok, hur vill du att fasen skall bete sig?
Mvh
Peter
PappaBas skrev:Kanske det skulle skrivas lite om skillnaderna mellan minimum fas, linjär fas,grupplöptid och hörbarhet av fasdistorition?
Svante skrev:(Jag ogillar uttrycket fasdistorsion, eftersom det antagligen är fasvridning som avses. Fasvridning är en linjär egenskap och bör därför inte kallas distorsion IMHO.)
Bill50x skrev:Svante skrev:(Jag ogillar uttrycket fasdistorsion, eftersom det antagligen är fasvridning som avses. Fasvridning är en linjär egenskap och bör därför inte kallas distorsion IMHO.)
Men även linjära förändringar är väl dist? Kallas väl för linjär dist jmf med olinjär sådan - eller?
/ B
sebatlh skrev:I sånt fall måste man kalla exempelvis ett högpassfilter för dist med. Eller för den delen högtalare som inte spelar den djupaste djupbasen för "distande högtalare".Bill50x skrev:Men även linjära förändringar är väl dist? Kallas väl för linjär dist jmf med olinjär sådan - eller?Svante skrev:(Jag ogillar uttrycket fasdistorsion, eftersom det antagligen är fasvridning som avses. Fasvridning är en linjär egenskap och bör därför inte kallas distorsion IMHO.)
Rent tekniskt är det kanske korrekt men språkligt blir det lite klumpigt.
Bill50x skrev:sebatlh skrev:I sånt fall måste man kalla exempelvis ett högpassfilter för dist med. Eller för den delen högtalare som inte spelar den djupaste djupbasen för "distande högtalare".Bill50x skrev:Men även linjära förändringar är väl dist? Kallas väl för linjär dist jmf med olinjär sådan - eller?Svante skrev:(Jag ogillar uttrycket fasdistorsion, eftersom det antagligen är fasvridning som avses. Fasvridning är en linjär egenskap och bör därför inte kallas distorsion IMHO.)
Rent tekniskt är det kanske korrekt men språkligt blir det lite klumpigt.
Som du beskriver det håller jag med. Men tänk riaa-korrektion i ett phonosteg. En avvikelse på några dB vid brytfrekvenserna borde väl klassificeras som dist?
Jag menar nog snarare så att en medveten förändring av en tonkurva är korrigering (tex tonkontroller, filter osv) medan icke önskad förändring (tex i en förstärkares frekvensgång) är dist.
/ B
paa skrev:Distordera betyder förvränga. Det går utmärkt att förvränga tonkurvan, men det är inte så ordet brukar användas, och det kommer bara att skapa förvirring.
Svante skrev:Ja, och man kan förvränga volymen också, men inte heller det är distorsion.paa skrev:Distordera betyder förvränga. Det går utmärkt att förvränga tonkurvan, men det är inte så ordet brukar användas, och det kommer bara att skapa förvirring.
Bill50x skrev:Svante skrev:Ja, och man kan förvränga volymen också, men inte heller det är distorsion.paa skrev:Distordera betyder förvränga. Det går utmärkt att förvränga tonkurvan, men det är inte så ordet brukar användas, och det kommer bara att skapa förvirring.
Definitionsmässigt, jo. Om ett fonogram inte återges i skala 1:1 i alla avseenden, då har man dist. Detta är hårdraget men tänk tanken hela vägen. OM vi nu accepterar "disten" lägre volym, vilka annan dist kan vi acceptera som beror av denna lägre volym?
/ B
schmutziger skrev:den här tråden har börjat att dista lavinartat...
hur väljer man tex komponenter map tex effekttålighet?
hur mäter man på bra sät`t är väl också relevant?
Det kan väl vara ett första ordningens Bessel också? Även om dom råkar vara identiska.aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
aisopos skrev:schmutziger skrev:den här tråden har börjat att dista lavinartat...
hur väljer man tex komponenter map tex effekttålighet?
hur mäter man på bra sät`t är väl också relevant?
Jag håller med om disten.
Men jag undrar lite också över de olika filtertopologierna; Butterworth, bessel, Chebyshev och L-R + ev andra jag inte vet...
Vad skiljer och varför ska man välja en före en annan?
Bill50x skrev:Svante skrev:Ja, och man kan förvränga volymen också, men inte heller det är distorsion.paa skrev:Distordera betyder förvränga. Det går utmärkt att förvränga tonkurvan, men det är inte så ordet brukar användas, och det kommer bara att skapa förvirring.
Definitionsmässigt, jo. Om ett fonogram inte återges i skala 1:1 i alla avseenden, då har man dist. Detta är hårdraget men tänk tanken hela vägen. OM vi nu accepterar "disten" lägre volym, vilka annan dist kan vi acceptera som beror av denna lägre volym?
/ B
Svante skrev:(Jag ser framför mig hur Bill50x drar upp volymen, någon ropar "F*N VAD DET DISTAR", Bill50x svarar "JA, VISST ÄR VOLYMEN HÖG?")
Svante skrev:(Jag ser framför mig hur Bill50x drar upp volymen, någon ropar "F*N VAD DET DISTAR", Bill50x svarar "JA, VISST ÄR VOLYMEN HÖG?")
Bill50x skrev:Och var i sammanhanget lägger vi "färgning"?
Nattlorden skrev:Bill50x skrev:Och var i sammanhanget lägger vi "färgning"?
Färgning och dist är i min bok synonymer. Färgning upplevs säkert som ett vänligare ord av majoriteten.
Svante skrev:aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
Ja. Och Bessel, och Chebychev.
Ett första ordningen filter kan bara ha en enda typ av överföringsfunktion. Det enda som kan skilja är brytfrekvensen.
De olika filtertyperna (butterworth, bessel, etc) är olika sätt att optimera tonkurvan för filtret, exklusive brytfrekvensen. För första ordningens filter finns inget kvar att optimera och alla filter blir lika. Till och med ett första ordningens Svantefilter måste vara likadant.
paa skrev:Svante skrev:aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
Ja. Och Bessel, och Chebychev.
Ett första ordningen filter kan bara ha en enda typ av överföringsfunktion. Det enda som kan skilja är brytfrekvensen.
De olika filtertyperna (butterworth, bessel, etc) är olika sätt att optimera tonkurvan för filtret, exklusive brytfrekvensen. För första ordningens filter finns inget kvar att optimera och alla filter blir lika. Till och med ett första ordningens Svantefilter måste vara likadant.
Men hur blir första ordningens seriefilter då?
paa skrev:Svante skrev:aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
Ja. Och Bessel, och Chebychev.
Ett första ordningen filter kan bara ha en enda typ av överföringsfunktion. Det enda som kan skilja är brytfrekvensen.
De olika filtertyperna (butterworth, bessel, etc) är olika sätt att optimera tonkurvan för filtret, exklusive brytfrekvensen. För första ordningens filter finns inget kvar att optimera och alla filter blir lika. Till och med ett första ordningens Svantefilter måste vara likadant.
Men hur blir första ordningens seriefilter då?
Svante skrev:aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
Ja. Och Bessel, och Chebychev.
Ett första ordningen filter kan bara ha en enda typ av överföringsfunktion. Det enda som kan skilja är brytfrekvensen.
De olika filtertyperna (butterworth, bessel, etc) är olika sätt att optimera tonkurvan för filtret, exklusive brytfrekvensen. För första ordningens filter finns inget kvar att optimera och alla filter blir lika. Till och med ett första ordningens Svantefilter måste vara likadant.
Svante skrev:I kokboksfiltervärlden är det rätt klart att udda ordningens filter ska vara butterworth och jämna ordningens filter ska vara kvadratiskt Butterworth (=Linkwitz-Riley). Det är enda sättet* att få |H(jw)|=1, alltså att alla frekvenser kommer igenom lika starkt.
Bill50x skrev:Nattlorden skrev:Bill50x skrev:Och var i sammanhanget lägger vi "färgning"?
Färgning och dist är i min bok synonymer. Färgning upplevs säkert som ett vänligare ord av majoriteten.
I min värld (baserad på hur åsikter uttrycks bland annat här) är färgning lika med frekvensgångsskillnader medan dist är resten, dvs olinjära förändringar.
/ B
IngOehman skrev:Svante skrev:I kokboksfiltervärlden är det rätt klart att udda ordningens filter ska vara butterworth och jämna ordningens filter ska vara kvadratiskt Butterworth (=Linkwitz-Riley). Det är enda sättet* att få |H(jw)|=1, alltså att alla frekvenser kommer igenom lika starkt.
Ingalunda!
Det vill säga, med reservation för att jag inte missförstår dig.
Det finns faktiskt ett oändligt antal kombinationer av filter som tillsammans
(summerade) ger en rak tonkurva.
För varje filterhalva finns det dessutom oändligt många filterhalvor som det
går att kombinera med - och få rak tonkurva!
Även om man förutsätter att filtrets halvor är symmetriska med varandra
(vilket det väl egentligen inte finns skäl att förutsätta) så finns det dock
andra sorts filter än de du nämnde, som tillfredsställer att |H(jw)|=1.
Igen - sagt med reservation för att jag kan ha missförstått eller missat
något av det du skrev.
Vh, iö
aisopos skrev:Ett chebychev sägs ju dela brantare och med mer rippel i passbandet.
Så ett 1'a ordningens chebychev delar brantare och med mer rippel än en ett 1'a ordningens butterworth?
Eller var det också en tumregel jag ska kasta?
(Jag har inga tummar kvar ...)
jonasp skrev:"Computers are useless. They can only give answers" - Pablo Picasso
Bill50x skrev:Nattlorden skrev:Bill50x skrev:Och var i sammanhanget lägger vi "färgning"?
Färgning och dist är i min bok synonymer. Färgning upplevs säkert som ett vänligare ord av majoriteten.
I min värld (baserad på hur åsikter uttrycks bland annat här) är färgning lika med frekvensgångsskillnader medan dist är resten, dvs olinjära förändringar.
/ B
Kraniet skrev:den här tråden verkar ju leva rätt bra av sig själv. Men då flera verkar efterlysa feedback från trådskaparen (mig) så gör jag det.
Tycker Peter Bremen, Svante och Öhman börjat bra. Kanske komplimenterar dessa tre varandra rätt så bra. Peters bild är ju föredömligt illustrerande när det kommer till vågens utseende och hur detta med fas relaterar.
...
Här kommer då frågan om vilka egenskaper man vill/bör ha också bli aktuell. Kanske är det enklaste att behandla det elektriska först. Sedan de akustiska egenskaperna och hur olika filter tacklar dessa saker.



IngOehman skrev:Ja, det är möjligt att han tänkte sig en värld där bara Butterworth- och
LR-filter finns. Men även skolböcker kan ju innehålla flera filter-sorter än
så, och de kan även tala om att polerna kan flyttas godtyckligt för att
skapa även helt andra filter än sådana som har råkat fått namn.
Kanske inkluderade han också den reservationen när jag skrev:
"Det är enda sättet* att få |H(jw)|=1, alltså att alla frekvenser kommer
igenom lika starkt."
Jag tycker dock att "enda sättet" är lite missvisande om det var med de
där reservationerna som han menade, så jag ville bara klargöra att det går
att skapa spikrak tonkurva på en förfärligt massa olika sätt - i synnerhet
när man talar enkel endimensionell filter-addering*.
Vh, iö
- - - - -
*Högtalare adderar inte så, och en massa andra egenskaper än någon sorts
"nominell tonkurva" kan påverkas och påverkas MYCKET av även rätt så små
ändringar i filter. Talar om både spridningsegenskaper, distorsion och effekt-
tålighet.

Fjonkalicious skrev:Jag kommenterar inte metadebatten för det förlänger den bara.
IngOehman skrev:Kokböcker brukar inte innehålla så mycket om filter överhuvudtaget,
med notera bara undantag i form av t ex kaffefilter.
Vh, iö
petersteindl skrev:Jag kanske bör nämna att det finns andra typer av spiraler. Här är ett exempel.
Solros med frön ordnade i 21 spiraler medsols och 34 spiraler motsols ut från centrum framifrån betraktat. Naturen är bäst
Mvh
Peter

jonasp skrev:IngOehman skrev:Kokböcker brukar inte innehålla så mycket om filter överhuvudtaget,
med noterbara undantag i form av t ex kaffefilter.
Vh, iö
Åjo!
http://www.amazon.com/Loudspeaker-Desig ... 1882580109
paa skrev:Svante skrev:aisopos skrev:Ett första ordningen filter (6dB/okt) är väl alltid ett butterworth ?
Ja. Och Bessel, och Chebychev.
Ett första ordningen filter kan bara ha en enda typ av överföringsfunktion. Det enda som kan skilja är brytfrekvensen.
De olika filtertyperna (butterworth, bessel, etc) är olika sätt att optimera tonkurvan för filtret, exklusive brytfrekvensen. För första ordningens filter finns inget kvar att optimera och alla filter blir lika. Till och med ett första ordningens Svantefilter måste vara likadant.
Men hur blir första ordningens seriefilter då?
aisopos skrev:Ett chebychev sägs ju dela brantare och med mer rippel i passbandet.
Så ett 1'a ordningens chebychev delar brantare och med mer rippel än en ett 1'a ordningens butterworth?
Eller var det också en tumregel jag ska kasta?
(Jag har inga tummar kvar ...)
IngOehman skrev:Svante skrev:I kokboksfiltervärlden är det rätt klart att udda ordningens filter ska vara butterworth och jämna ordningens filter ska vara kvadratiskt Butterworth (=Linkwitz-Riley). Det är enda sättet* att få |H(jw)|=1, alltså att alla frekvenser kommer igenom lika starkt.
Ingalunda!
Det vill säga, med reservation för att jag inte missförstår dig.
Det finns faktiskt ett oändligt antal kombinationer av filter som tillsammans
(summerade) ger en rak tonkurva.
För varje filterhalva finns det dessutom oändligt många filterhalvor som det
går att kombinera med - och få rak tonkurva!
Även om man förutsätter att filtrets halvor är symmetriska med varandra
(vilket det väl egentligen inte finns skäl att förutsätta) så finns det dock
andra sorts filter än de du nämnde, som tillfredsställer att |H(jw)|=1.
Igen - sagt med reservation för att jag kan ha missförstått eller missat
något av det du skrev.
Vh, iö
Svante skrev:*Om flankerna i filtret ska motsvara filtrets ordningstal, dvs att ett 4:e ordningens filter ska luta med 24 dB/oktav i spärrbanden i båda filtergrenarna.
IngOehman skrev:jonasp skrev:"Computers are useless. They can only give answers" - Pablo Picasso
Förbaskat klokt sagt av honom!
IngOehman skrev:Du kan till och med ställa frågor till en sten.
Utmaningen är att skapa de viktiga frågorna.
Vh, iö
Svante skrev:Spänningsdelare för växelspänning, 1:a ordn LP, RC-filter:
- Kod: Markera allt
----
-----| |--------+----------
---- |
R |
|
-------
U1 C U0
-------
|
|
|
|
-------------------+----------
U0/U1=Zc/(Zr+Zc)=(1/jwC) / (R+1/jwC) =1/(1+jwRC)
Svante skrev:Ett andra ordningens delningsfilter:
- Kod: Markera allt
^^^
------ --------+------+---------
L | |
| |
| -
------- | |
U1 C | | R Ul
------- | |
| -
| |
| |
| |
-----------------+------+---------
Ul/U1=
=((1/jwC)//R) / (jwL + R//(1/jwC))=
=...=
=1 / ( 1 + jwL/R - w²LC)
Det kan kanske vara en fördel, det är inte alltid jag vill att allt skall summera till 1. Målkurvan kan vara nåt annat än ett rakt streck.Svante skrev: En HP och LP chebychev summerar inte till 1.
phon skrev:Det kan kanske vara en fördel, det är inte alltid jag vill att allt skall summera till 1. Målkurvan kan vara nåt annat än ett rakt streck.Svante skrev: En HP och LP chebychev summerar inte till 1.
^^^
------ --------+------+---------
L | |
| |
| -
------- | |
U1 C | | R Ul
------- | |
| -
| | |
R2 | | |
| | |
| <
< < L3
L2 < <
< |
| |
-----------------+------+---------
________________
\
\
\
\
\____________paa skrev:phon skrev:Det kan kanske vara en fördel, det är inte alltid jag vill att allt skall summera till 1. Målkurvan kan vara nåt annat än ett rakt streck.Svante skrev: En HP och LP chebychev summerar inte till 1.
Vilket är den viktigaste avvikelsen från ett rakt streck på målkurvan, skulle du säga?
Martin skrev:Man kan ju också, även om de är akademiskt intressanta, frångå specialfallen lustiganamnfiltrena och justera på fri hand.
Martin skrev:
- Kod: Markera allt
^^^
------ --------+------+---------
L | |
| |
| -
------- | |
U1 C | | R Ul
------- | |
| -
| | |
R2 | | |
| | |
| <
< < L3
L2 < <
< |
| |
-----------------+------+---------
Ul/U1=
=((1/jwC+R2+jwL2)//(R+jwL3) / (jwL + (R+jwL3)//(1/jwC+R2+jwL2))
Martin skrev:
- Kod: Markera allt
________________
\
\
\
\
\____________
Du måste hålla med om att de är alla döpta efter herrar med lustiga namn. Finns många tillämpningar för sådana filter rakt av, men i många fall kan de behöva justeras och finputsas efter andra önskemål, löptidsfasskillnad mellan element kan vara en sådan.Morello skrev:Martin skrev:Man kan ju också, även om de är akademiskt intressanta, frångå specialfallen lustiganamnfiltrena och justera på fri hand.
"Lustiganamnfilter" låter lite respektlöst.
Har du verkligen studerat dessa filter och förstått vad som kännetecknar dem?
IngOehman skrev:- - - - -
....
STEREOSYSTEMFEL*
...
*För den konstruktör som förstår dem/bryr sig om dem/tror på dem.
Jocke skrev:Martin skrev:
- Kod: Markera allt
^^^
------ --------+------+---------
L | |
| |
| -
------- | |
U1 C | | R Ul
------- | |
| -
| | |
R2 | | |
| | |
| <
< < L3
L2 < <
< |
| |
-----------------+------+---------
Ul/U1=
=((1/jwC+R2+jwL2)//(R+jwL3) / (jwL + (R+jwL3)//(1/jwC+R2+jwL2))
Antar att R och L3 i det här fallet är elementets impedans.Martin skrev:
- Kod: Markera allt
________________
\
\
\
\
\____________
Undrar varför jag inte kan spåra L2 i kurvan...?
Kraniet skrev:ja jag tycker inte detta med de definierade filterfunktionerna är mer intressant än som riktlinjer.
tex har mina nuvarande alster filterkurvor som liknar 3e ordningens L/R. Nu säger nån att det inte finns 3e ordningens L/R och det är väl sant. Men i LspCad kan man optimera för sådana kurvor.
Men vad det ger för effekt på off-axis kurvor och energiutstrålning osv vet jag ju inte. Jag har ju använt det som får de två elementen att komma ihop på bästa sätt helt enkelt. Det finns säkert andra sätt förstås.
Det vet jag ju inte hur de andra olika filtren Butterworth, L/R, Bessel osv gör heller så det kvittar kanske.
I simuleringsprogrammet tittar jag på hur fasen mellan de två elementen stämmer. Har fått för mig att de bör följa varandra vid och något utanför delningen. Så jag optimerar detta tills de följer varandra exakt. Samtidigt tittar jag på frekvensgången on-axis och off-axis. Lober blir det ju i vertikalled och där har jag i brist på bättre vetande optimerat för en stor lob rakt fram och accepterat utsläckningen som verkar oundviklig off-axis.
Jocke skrev: Vi har ju hört expertisen hävda att man kan utläsa det mesta man behöver veta av tonkurvan. En rutinerad konstruktör nämnde nyligen att han knappt beräknar eller simulerar sina konstruktioner. Tydligen kan man komma rätt långt med erfarenhet och mätningar!
Tror tom att man hantverksmässigt kan tillverka en högtalare som spelar musikaliskt - frågan är om man kan beräkna eller simulera fram en sådan?^^
PappaBas skrev:
Jo inom medicin pratar man om något som kallas "pattern recognition" dvs väldigt erfarna och gamla läkare kan diagnosticera saker väldigt precist och med hög träffsäkerhet bara genom att nästan titta på patienten och ställa få frågor. Det betyder inte att en som är ny kan göra på samma sätt utan den förmågan infinner sig nog efter kanske ett liv i yrket där man sett tusentals människor.
Tror man kan säga samma sak om en skicklig konstruktör. Men det går inte att hoppa direkt till det utan man måste ta sig igenom den snåriga och krokiga lärandets stig...
Själv tycker jag om att ha lite sådana småproblem att brottas med. Det tjänar som avslappning på tråkiga bussturer om inte annatDet är förbaskat kul när man förstår något!
PappaBas skrev:Jocke skrev: Vi har ju hört expertisen hävda att man kan utläsa det mesta man behöver veta av tonkurvan. En rutinerad konstruktör nämnde nyligen att han knappt beräknar eller simulerar sina konstruktioner. Tydligen kan man komma rätt långt med erfarenhet och mätningar!
Tror tom att man hantverksmässigt kan tillverka en högtalare som spelar musikaliskt - frågan är om man kan beräkna eller simulera fram en sådan?^^
Jo inom medicin pratar man om något som kallas "pattern recognition" dvs väldigt erfarna och gamla läkare kan diagnosticera saker väldigt precist och med hög träffsäkerhet bara genom att nästan titta på patienten och ställa få frågor. Det betyder inte att en som är ny kan göra på samma sätt utan den förmågan infinner sig nog efter kanske ett liv i yrket där man sett tusentals människor.
Tror man kan säga samma sak om en skicklig konstruktör. Men det går inte att hoppa direkt till det utan man måste ta sig igenom den snåriga och krokiga lärandets stig...
Själv tycker jag om att ha lite sådana småproblem att brottas med. Det tjänar som avslappning på tråkiga bussturer om inte annatDet är förbaskat kul när man förstår något!
phon skrev:Det kan kanske vara en fördel, det är inte alltid jag vill att allt skall summera till 1. Målkurvan kan vara nåt annat än ett rakt streck.Svante skrev: En HP och LP chebychev summerar inte till 1.
Morello skrev:Martin skrev:Man kan ju också, även om de är akademiskt intressanta, frångå specialfallen lustiganamnfiltrena och justera på fri hand.
"Lustiganamnfilter" låter lite respektlöst.
Svante skrev:Morello skrev:Martin skrev:Man kan ju också, även om de är akademiskt intressanta, frångå specialfallen lustiganamnfiltrena och justera på fri hand.
"Lustiganamnfilter" låter lite respektlöst.
Det finns ju en filtertyp som är alldeles extra bra om man går en filterkurs och vill ha högt betyg. Alltså, det har ett ganska bra smörvärde.
Jocke skrev:Martin skrev:Man kan ju också, även om de är akademiskt intressanta, frångå specialfallen lustiganamnfiltrena och justera på fri hand.
Formeln för det???
Jocke skrev:Det där tycker jag verkar vara en genomarbetad metodik med ett tydligt och definierbart mål! Knappas att "justera på fri hand"...eller?^^
Oavsett vilken formel man använder och hur man formulerar den är det ju fortfarande skolboksfilter... "Att justera på fri hand" handlar ju om hantverk och erfarenhet och den är nog svår att räkna ut... (innan man fått ännu mer erfarenhet möjligen)!
Jocke skrev:Det där tycker jag verkar vara en genomarbetad metodik med ett tydligt och definierbart mål! Knappas att "justera på fri hand"...eller?^^
Oavsett vilken formel man använder och hur man formulerar den är det ju fortfarande skolboksfilter... "Att justera på fri hand" handlar ju om hantverk och erfarenhet och den är nog svår att räkna ut... (innan man fått ännu mer erfarenhet möjligen)!
skrutten skrev:Jocke skrev:Det där tycker jag verkar vara en genomarbetad metodik med ett tydligt och definierbart mål! Knappas att "justera på fri hand"...eller?^^
Oavsett vilken formel man använder och hur man formulerar den är det ju fortfarande skolboksfilter... "Att justera på fri hand" handlar ju om hantverk och erfarenhet och den är nog svår att räkna ut... (innan man fått ännu mer erfarenhet möjligen)!
Att justera på frihand är som du skriver förståss baserat på erfarenhe.t Jag har t.ex. en heldel erfarenhet runt mina egna filter så jag vet vart jag ändrar iaf ett mindre antal parametrar. Men detta är likfullt ett sidospår om man inte berättar vad som styr vad... Att det är svårt att räkna ut, svar nej - det gör ju datorn. När man jobbar med ett filter uppstår detta hela tiden att man ändrar på något som man tycker behöver ändras på pågrund av att det låter på något visst sätt och vips så blir det ett hantverk?
rotel2 skrev:På vilket avstånd mäter ni (om ni nu gör det) för att få med "baffelsteget" ? Iaf på
ett avstånd så man kan ana när/vid vilken frekvens det börjar falla.
Naqref skrev:rotel2 skrev:På vilket avstånd mäter ni (om ni nu gör det) för att få med "baffelsteget" ? Iaf på
ett avstånd så man kan ana när/vid vilken frekvens det börjar falla.
Minst dubbla baffelbredden.
Svante skrev:Jocke skrev:Det där tycker jag verkar vara en genomarbetad metodik med ett tydligt och definierbart mål! Knappas att "justera på fri hand"...eller?^^
Oavsett vilken formel man använder och hur man formulerar den är det ju fortfarande skolboksfilter... "Att justera på fri hand" handlar ju om hantverk och erfarenhet och den är nog svår att räkna ut... (innan man fått ännu mer erfarenhet möjligen)!
Poängen jag försöker få fram är att om man begriper kokboksfiltren så är man bättre rustad för handpåläggning. Syftet med att begripa kokboksfiltren är inte att bygga just sådana.
Jocke skrev:Men det här med maximalt flat är kanske inte det som spelar musik så att det låter bra?
IngOehman skrev:Svante skrev:Poängen jag försöker få fram är att om man begriper kokboksfiltren så är man bättre rustad för handpåläggning. Syftet med att begripa kokboksfiltren är inte att bygga just sådana.
Jag håller på sätt och vis med dig, någonstans måste man börja.
Men jag undrar ändå varför några få specialfall skall få särskild uppmärk-
samhet redan sådär i första kapitlet?
Är det verkligen enklare att lära sig att "förstå" ett filter när det har en
specifik kokboksdimensionering?
Varför är 0,707 lättare att förstå än säg 0,6?
phon skrev:Här är ett enkelt filter till en diskant, kan kanske reverse-engineras?
grafpro skrev:Jocke skrev:Men det här med maximalt flat är kanske inte det som spelar musik så att det låter bra?
Jo, definitivt - det är hela ändamålet med filter, vad skulle det annars vara? Jämn tonkurva i frifält, ner till kanske 300Hz (därunder anpassat till den tänkta placeringen i rummet) är steg ett.
Elementval som ger låg dist är steg två.
Den ortoakustiske vill också att spridningen är sådan att det reflekterade ljudet i rummet har jämn tonkurva.
Om inte det är ändamålet så pratar vi inte hifi, men det är sant att hifi inte alltid är målet.
Svante skrev:Och en maximalt platt tonkurva känns ju mer relevant än en optimalt faslinjär kurva, sådär allmänt i audiosammanhang.
Användare som besöker denna kategori: Bing [Bot] och 21 gäster