Om man ställer upp ekvationen för resonansvilligheten (Q-värdet) så ser man enkelt hur Q-värdet kan påverkas i olika riktningar.
Så här ser det ut:
Qt = SQR((ke+kl)*Mm) / (Dm+Dl+(BL^2/(Re+Rg)))
Eller en bild är mycket bättre så man slipper alla onödiga parenteser:
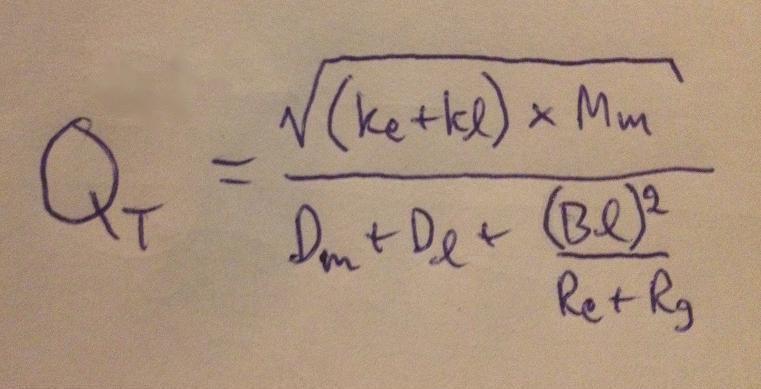
I ekvationen är:
ke =
elementets konupphängningsstyvhet - N/m
kl = fjädringsstyvheten från
lådan - N/m
Mm = rörliga
massan (kon + medsvängande luft) - kg
Dm =
mekaniska
dämpningen i upphängningen - Ns/m
Dl = mekaniska
dämpningen från
lådan - Ns/m
B = magnetiska flödestätheten i spalten - T (N/(Am))
l = längen av talspoletråden som är i spalten - m
Re = talspolens resistans - ohm
Rg = generatorimpedansen(resistansen) från förstärkare + kabel - ohm
Om man vill veta hur alla dessa variabler påverkar Q-värdet så är det bara att titta på hur de verkar i ekvationen.
Möjligen kan man addera en ekvation till om man ogillar att se lådans fjädring som en variabel, och hellre tycker att det är lådans volym (och dämpning) som är variablerna. Den ekvationen ser ut såhär:
kl = 142800*Sd^2 / V
I ekvationen är:
142800 = antingen produkten av luftens densitet och densammas ljudhastighet, eller produkten mellan lufttrycket och luftens adiabatiska komprimerbarhetskonstant. Den senare sjunker från cirka 1,4 och mot 1,0 när lådans volym är 100 % isotermiserad.
Sd = effektiv membranarea - m^2
V = lådans volym - m^3
- - -
Exempel:
Öka lådans volym till det dubbla ger en halvering av kl, vilket kommer att sänka Q-värdet, eftersom k är en resonansfaktor och inte en dämpfaktor. Hur mycket Q minskar beror på i vilken grad kl dominerar över ke. Vilket i sin tur kan sägas det det beror på i vilken grad V dominerar över Vas (som = 142800 * Sd^2 / ke).
Att addera dämpmaterial i lådan sänker Q på två sätt - Det adderar dämpning (Dl) och det isotermiserar och ökar alltså virtuella lådvolymen, och sänker således kl. Adderas dämpmaterialet nära elementet så påverkar det proportionellt sett mera via Dl.
Att addera massa till konen ökar Q-värdet, eftersom Mm är en resonansfaktor.
Att skära bort en del av upphängningen sänker Q-värdet eftersom man då minskar en resonansfaktor.
Att lägga till en magnet som trycker in mera fält i spalten minskar Q-värdet eftersom det ger en större elektromagnetisk dämpning.
Att addera seriemotstånd ökar Q-värdet, eftersom det minskar den elektromagnetiska dämpningen.
Och så vidare...
Vh, iö
- - - - -
PS. Naturligtvis är det ovanstående illa förenklat då det i princip bara säger något om hur ett element beter sig i sluten låda och faktorer som t ex Le (talspoleinduktansen) som även den påverkar ett elements resonansbeteenden genom samverkan med Mm. En annan faktor som fattas är hur dämpmaterial i lådor kan ge en missanpassning med avseende på den akustisk impedans (frekvensberoende dessutom) således att man faktiskt kan få en höjning av Q vid ökning av mängden dämpning i vissa sammanhang. Men förhoppningsvis ger det i varje fall en susning om hur vissa av de fundamentala egenskaperna hänger samman. Men som brasklapp vill jag ha sagt att det på riktigt är mera komplicerat och vissa av parametrarna egentligen inte är diskreta utan distribuerade. På det kommer olinjära beteenden som inte adresseras alls i det ovanstående. Och mycket annat.
Fd psykoakustikforskare & ordf LTS. Nu akustiker m specialiteten
studiokontrollrum, hemmabiosar & musiklyssnrum. Även Ch. R&D
åt Carlsson och Guru, konsult åt andra + hobbyhögtalartillv (Ino).
