3. STATISTISKA SIGNIFIKANSTEST
Vi inleder med följande lilla jakthistoria:
- Jag satt ute på pass i helgen när det kom en älg förbi.
Jag skulle just till att skjuta då det plötsligt dök upp
en björn som började gör utfall mot älgen!
Jag visste inte riktigt vad jag skulle göra.
- Det var som sjutton! Vad gjorde älgen?
- Den klättrade upp i ett träd!
- Men älgar kan väl inte klättra i träd?!
- Nej, jag vet.
Men vad fan skulle den göra?
Statistiska signifikanstest åläggs ofta uppgifter de egentligen inte kan lösa. Det gäller främst möjligheten att utifrån insamlad data uttala sig om de mekanismer som genererar data. Att gå från det ”partikulära” (de fall man verkligen undersöker) till det ”generella” (lagbundenheter som genererar utfallen) är inte oproblematiskt. Minst sagt. Och det är ingen slump att det kallas signifikanstest och inte ”konfidenstest”.
Att något är STATISTISKT SIGNIFIKANT kommer av engelskans
significant som betyder ungefär ”betydelsefull”, ”viktig” eller ”värd att lägga märke till”. Begreppet populariserades av R A Fisher under 1920-talet då den moderna doktrinen för signifikanstest grundlades. Andra viktiga bidrag kom då från bl.a. Jerzy Neuman och Egon Pearson. Den grundläggande tolkningen av sannolikhet som ligger till grund för deras arbeten är RELATIV FREKVENS. Det som avgör om ett resultat är STATISTISKT SIGNIFIKANT är om det i statistisk mening är ovanligt. Vi kan ta ett exempel.
Den som sett matcher från den amerikanska basketligan NBA kan inte ha undgått att lägga märke till att genomsnittslängden och variationen kring detta genomsnitt skiljer sig från övriga befolkningen – de flesta är runt 2 meter. Men det finns även spelare kring 1,75 m som regelbundet ”dunkar” bollen. Om vi drar ett slumpmässigt urval bland spelarna i NBA finns det en liten, men dock, chans att vi får en samling spelare som alla mäter mellan 1,75 och 1,85 och som vi inte skulle uppfatta som representativa för spelare i NBA som grupp betraktat. Om vi vet medellängden och hur populationen av spelare är fördelade runt detta medelvärde så kan vi beräkna sannolikheten för att få ett urval med en medellängd som avviker med ett visst värde från det sanna medelvärdet för alla spelare i NBA. Fördelningar av naturliga fenomen följer ofta en mindre samling matematiskt väldefinierade funktioner, vilket underlättar beräkningarna.
Om vi däremot försöker uttala om populationens egenskaper utifrån vårt urval stöter vi på patrull. Om vi inte känner till populationens sanna egenskaper så är data från vårt urval det enda vi har att gå på. Men hur kan vi veta om urvalet är representativt? Svaret är förstås: det vet vi inte. Det enda vi kan uttala oss om hur sannolikt ett visst urval är utifrån ANTAGANDEN om egenskaper hos populationen. Och det är precis vad ett SIGNIFIKANSTEST gör: hur (o)sannolikt är ett visst resultat givet vissa ANTAGANDEN om populationens egenskaper? Repris: ett statistiskt SIGNIFIKANT resultat är ett resultat som är statistiskt ovanligt och därför värt att lägga märke till.
Ett vanligt förförande vid hypotestestning går till på följande sätt:
1a. Ställ upp en nollhypotes (H0), som är den hypotes som skall testas
1b. Ställ upp en alternativ hypotes (uttalad eller outtalad) som är nollhypotesens komplement, dvs. INTE H0.
2. Genomför ett statistiskt test av nollhypotesen
3. Tillämpa en beslutsregel som avgör under vilken sannolikhetsnivå som du skall förkasta nollhypotesen. Välj den lägsta av flera standardiserade nivåer (t.ex. 0,01 eller 0,05) som den erhållna sannolikheten underskrider.
Litteraturen kring signifikanstest är inte samstämmig, i synnerhet inte om man går till urkällorna. Det gäller främst alternativhypotesens ställning och tillämpandet av en eventuell beslutsregel. Den ovanstående processen är det ”moderna” gängse sättet att gå tillväga men stöds faktiskt inte av någon av de grundläggande ”skolorna” inom signifikanstest (R A Fisher och Neyman/Pearson). Man kan kritiskt säga att man tagit det bästa (eller sämsta) av två världar och format en oheliga allians.
För att återgå till vårt basketexempel kan vi tänka oss att vi av olika anledningar (teori, observationer) vill testa om medellängden för spelare i NBA är MINST 2,00 meter. Detta är vår nollhypotes. Att ”noll” ingår i nollhypotesen har inget med ”ingen effekt” eller ”inget resultat” att göra utan kommer av engelskans ”null hypothesis”. Detta bör snarare tolkas som ett slags grundantagande eller ”baseline”. I vårt hypotetiska fall blir vår implicita alternativa hypotes att medelvärdet MINDRE är 2,00 meter.
UTVIKNING
Det skall sägas att nollhypoteser ofta är utformade i termer av ”ingen effekt” eller "ingen skillnad". Den alternativa hypotesen blir då ”någon effekt” eller "någon skillnad" men utan att man specificerar ett värde på hur stor effekten eller skillnaden är. Detta är praktiskt om man inte har särskilda skäl att definiera en viss effektstorlek.
Själva signifikanstestet i vårt exempel går till så att vi räknar ut sannolikheten för vårt urval under antagandet att det sanna medelvärdet är 2,00 meter eller mer. Om det skull slumpa sig så att vi får ett urval med många spelare under medellängd kommer våra beräkningar visa att det är mycket osannolikt att urvalet kommer från en population med det medelvärde över 2,00 m. Rent hypotetiskt kan vi säga att sannolikheten är 0,02 för vårt erhållna urval. Lika hypotetiskt tillämpar vi en beslutregel som säger ”förkasta nollhypotesen om sannolikheten för resultatet (p) är mindre än 0,05. Eftersom 0,02 är mindre än 0,05 förkastar vi nollhypotesen. Logiskt sett har vi inget annat att välja på än att behålla den alternativa hypotesen, nämligen att medelängden bland spelarna i den amerikanska basketligan är UNDER 2,00 m. Vi har inte bevisat något i strikt mening,
men vad fan ska man göra.
Här har vi valt ett exempel där beslutsregeln leder till ett felaktigt beslut. Vi har förkastat en sann nollhypotes och gör oss därför skyldiga till ett beslutsfel av typ 1. Men så var vårt urval också osannolikt.
När det gäller F/E-tester bygger de flesta redovisade uträkningarna på kombinatorik. För att öka förståelsen kan vi istället angripa problemet med en PARAMETRISERAD modell där den hypotetiska oändliga populationen karaktäriseras av en central tendens (medelvärde) och ett spridningsmått (varians eller standardavvikelse), dvs. populationens PARAMETRAR. Den relevanta sannolikhetsfunktionen för en variabel som kan anta värdena 1 eller 0 med sannolikheterna
p respektive
1-p kallas
binomialfunktionen. Medelvärdet för ett försök är p och variansen för ett försök är p*(1-p). För en serie med
n försök blir medelvärdet n*p och variansen n*p*(1-p).
Om vi har en variabel med värdena 0 (fel) och rätt (1) kommer en helt slumpmässig process att generera ett långsiktigt medelvärdet på 0,5 för varje försök. Om vi vill undersöka om en serie försök kommer från en population som INTE har ett medelvärdet på 0,5, dvs INTE kommer från en helt slumpmässig process, kan vi ställa upp följande hypoteser.
H0: Det sanna medelvärdet = 0,5
HA: Det sanna medelvärdet är INTE 0,5
Binomialfunktionen tecknas på detta sätt:
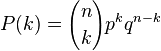
(1)
Tolkningen är att sannolikheten
P att få exakt
k ”rätt” i en serie försök beror av hur många försök man gör (
n), hur stor sannolikheten
patt få ”rätt” är i varje försök, samt hur stor sannolikheten
q är att svara fel.
q=1-p (2)
och
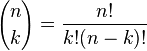
(3)
Vi kan här lägga märke till att
p kan varieras. Vi skulle således kunna ställa upp en nollhypotes med valfritt värde på
p och är inte bundna till just 0,5 även om det är det enda förekommande i just F/E-lyssningar
ETT EXEMPEL
Vad är sannolikheten att få MINST 8 rätt i 9 försök om sannolikheten för att svara rätt i varje försök är 0,5. Vi måste då använda den KUMULATIVA sannolikhetsfunktionen. För kontinuerliga sannolikhetsfunktioner, exempelvis den klassiska normalfördelning, innebär detta arean under kurvan för sannolikhetsfunktionen, dvs. att den kumulativa sannolikhetsfunktionen eller sannolikhetsfördelningen är integralen av sannolikhetsfunktionen. För diskreta sannolikhetsfördelningar summera vi de enskilda sannolikheter som ges av sannolikhetsfunktionen.
I vårt fall blir den kumulerade sannolikheten att vi får MINST 8 av 9 rätt summan av sannolikheten att få 8 av 9 rätt PLUS sannolikheten att får 9 av 9 rätt, formellt ”P(k≥8 )”
För 8 av 9 rätt gäller
k=8
n=9
p=0,5
q=0,5
För 9 av 9 rätt gäller:
k=9
n=9
p=0,5
q=0,5
För den som är road är det bara att plugga in värdena formlerna (1) och (3) och summera. För den som är mindre road, finns färdiga kalkylatorer på nätet, t.ex.
http://stattrek.com/online-calculator/binomial.aspx
Svaret blir i alla fall 0,0195
Om vi tillämpar beslutsregeln att förkasta H0 om p är mindre än 0,05 så innebär resultatet minst 8 av 9 rätt att vi förkastar H0. Slutsatsen blir att våra försök INTE kommer från en hypotetisk oändlig population med medelvärdet 0,5, dvs. våra svar är inte helt slumpmässiga.
Skulle vi acceptera utfallen som innebär minst 8 av 9 FEL stiger den kumulerade sannolikheten till det dubbla, dvs. p=0,039, eftersom vi också kommer att acceptera resultat med "ett eller färre fel". Beslutet att förkasta H0 kvarstår dock.
Och sådär kan man hålla på…
ÖVERKURS
Centrala gränsvärdesteoremet ger att SUMMAN av en serie STATISTISKT OBEROENDE och IDENTISKT FÖRDELADE slumpvariabler (sk.
i.d.d., independently and identically distributed) tenderar att vara fördelade enlig normalfördelningen OBEROENDE av variablernas grundläggande fördelning. Om vi betraktar varje försök i en serie på 7 som en slumpvariabel kommer alltså fördelning av denna summa tendera mot normalfördelning. Tumregeln säger att när det ingår 20 försök i varje serie/testomgång kan man med acceptabelt resultat ersätta binomialfördelningen med normalfördelningen. Ju kortare serie, desto större fel får man genom att approximera binomialfördelningen med normalfördelningen. Fördelen är att normalfördelningen är markant mindre beräkningskrävande vid ökande serielängder.
För att summera några av de viktigaste punkterna i signifikanstest:
1. Ett signifikanstest provar hur sannolikt ett erhållet resultat är givet antaganden om parametrarnas värden, INTE sannolikheten för de parametrar som antas styra utfallen.
2. Statistiskt SIGNIFIKANTA resultat är resultat som är ovanliga, givet vissa antaganden om PARAMETERARNA (populationsegenskaper). Osannolika resultat är värda att lägga märke till. Förenklat: SIGNIFIKANT är det samma som OVANLIGT.
3. Desto ovanligare ett utfall är (dvs. har LÅG sannolikhet för att inträffa) desto HÖGRE är dess statistisk signifikans (ovanlighet).
4. Ett signifikanstest provar H0, men INTE den alternativa hypotesen HA.
5. Vi förkastar H0 på grundval av en BESLUTSREGEL och hur (o)sannolikt utfallet är.
6. (O)sannolikheten för ett utfall under antagandena i H0 är INTE det samma som hur sannolik den alternativa hypotesen är. Det beror dels på att vi formellt inte testar den alternativa hypotesen HA utan endast H0, dels på att det skulle innebära ”omvänd sannolikhet” vilket inte är förenligt med definitionen av sannolikhet som relativ frekvens, vilket är den definition som signifikanstest förutsätter.
En slutsats man bör dra är att användningen av ordet ”konfidens” för (1-p), tolkat som ”förtroende för den alternativa hypotesen”, inte har med signifikanstest att göra, hur gärna vi än skulle vilja.
Och älgar kan inte klättra i träd.
Frågor på det?
Nästa avsnitt kommer sannolikt att behandla hur man kan tänka kring signifikansvärden vid avbrutna serier. Grundidén är att det i t.ex. F/E-test inte handlar om att man förlänger en testserie i hopp om att uppnå ett statistiskt signifikant resultat utan att man förkortar en testserie som egentligen är längre när man väl har uppnått ett statistiskt signifikant resultat.
/DQ-20
PS: Jag vill upprepa att jag är mycket tacksam för påpekanden om:
1. Sakfel
2. Pedagogiska missgrepp. Indikationer på pedagogiska missgrepp är att du inte förstår inlägget, tycker det inte är tillräcklig informativt eller tycker det är FÖR informativt.
3. Jag hade velat använda tecken för "mer än" och "mindre än" men det tolkar forumprogramvaran som html-taggar och vägrar acceptera texten.
4. Möjligen genererar mitt basketexempel mer frågor än svar. Jag skall klura på det lite till.
 .
.
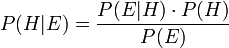
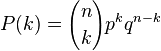 (1)
(1)
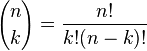 (3)
(3)