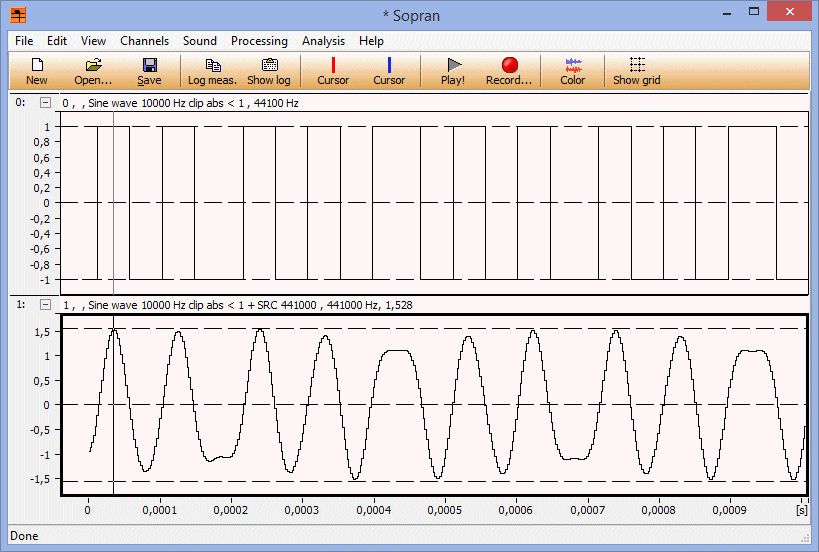
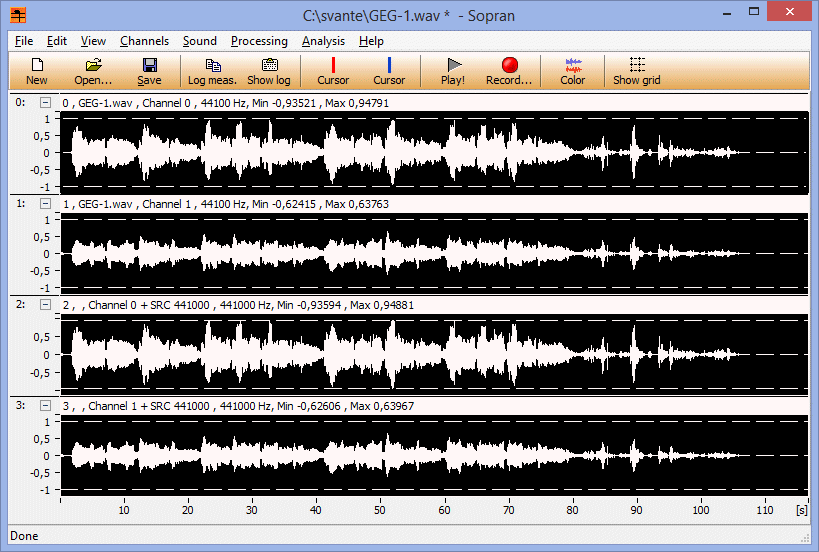
Jaha, jag tror nog att jag får betrakta försöket som avslutat med nya rekordet 7,01 ggr eller 16,9 dB. För att få till det tar jag samplingsfrekvensen 44100 Hz och en 22049 Hz sinus med amplituden 1000000000000 som jag klipper så att jag får en fyrkantvåg. Denna kommer att få vartannat sampel 1 och -1, utom 2 ggr per sekund när 1:an eller -1:an upprepar sig. Denna signal samplar jag sedan upp till 441000 Hz med ett interpolationsfilter med en sinc som är 20000 perioder lång.
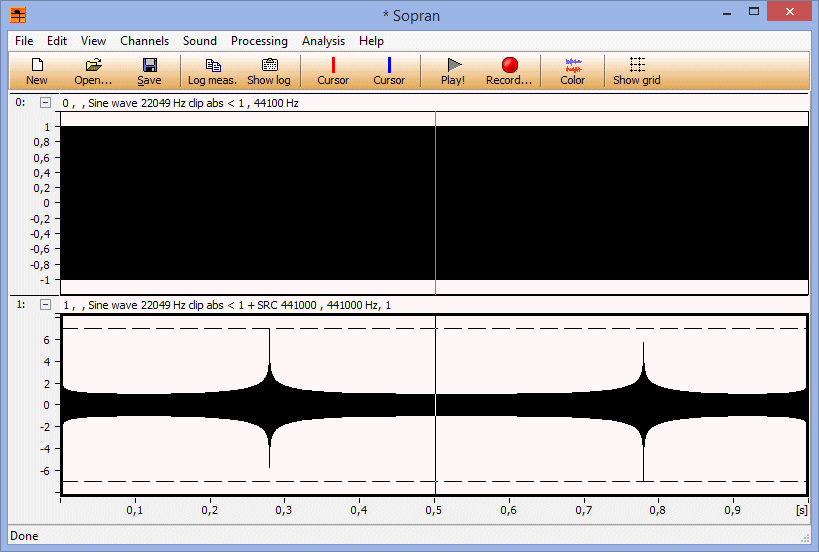
Det som sker i detta "worst case" är att signalen är vald sådan att varje sampel i impulssvaret för rekonstruktionsfiltret multipliceras med antingen 1 eller -1, så att amplituden blir summan av
absolutbeloppet för alla tapparna i filtret. Om man räknar mitt emellan samplen*, där sinusens amplitud i sinx/x är +1 eller -1 får man en summa som blir 4/pi*(1+1/3+1/5+1/7...) och den summan är oändlig om sincen är oändligt lång.
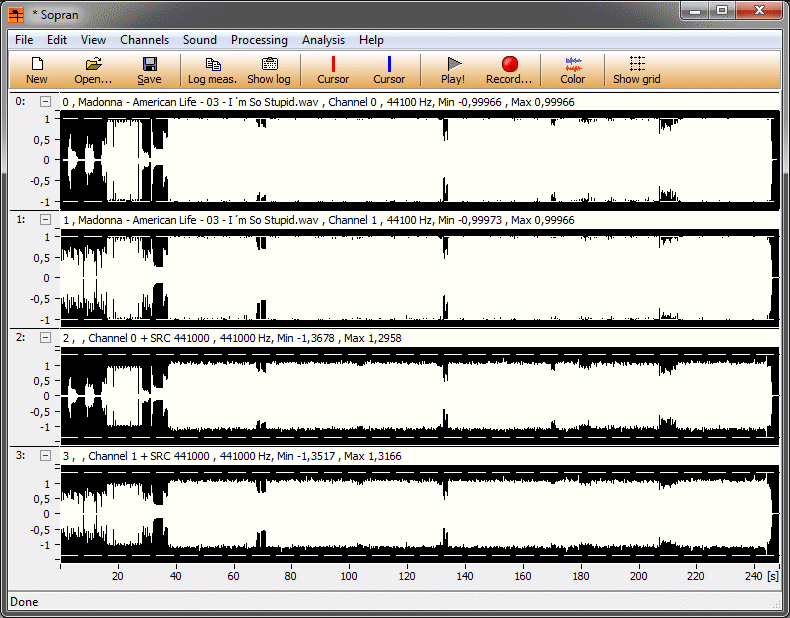
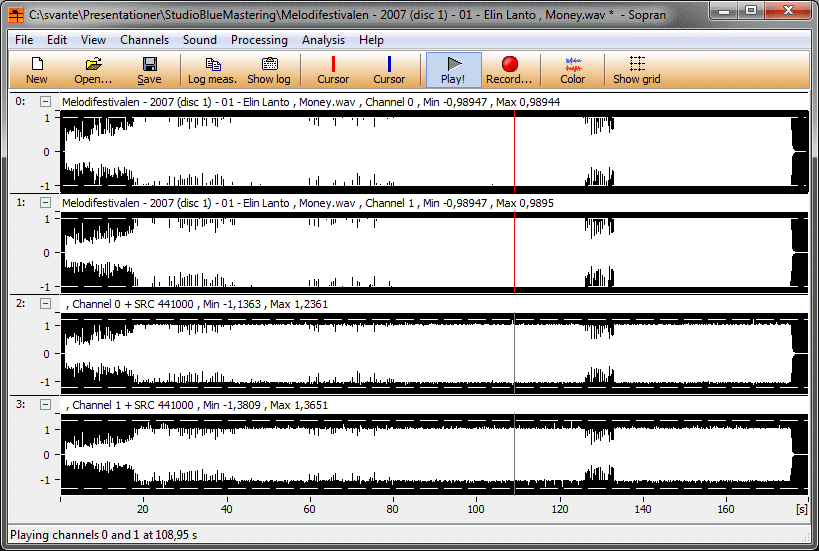
För praktiska implementationer med FIR-filter är dock impulssvaret ändligt och dessutom minskar amplituden "mot svansarna" typiskt fortare** vilket gör att summan blir ändlig. För varje implementation kan man alltså räkna ut ett "worst case" och det borde tillverkarna göra. Jag vet dock att de inte alltid gör det. Det brukar räcka med en fullt utstyrd fyrkantvåg för att de ska klippa, och det finns alltså ännu värre signaler.
Ja, så kan det gå när man håller monolog. Jag har funderat en hel del på detta, men det hjälpte att tänka högt i stället. Det känns lite som "case closed".
*Det är inte säkert att just detta läge ger maximal amplitud, men eftersom den ändå blir oändlig spelar det ingen roll för resonemanget.
**Detta är bra även på andra sätt, filterkaraktäristiken blir brantare så.
Så länge har jag längat efter att loudness war skulle vara över. Nu börjar jag tro att vi faktiskt är där. Kruxet är att vi förlorade.
Jag har inget att tillföra i ämnet, men det är kul att läsa.
