Någon som vet hur man designar en waveguide?

[paa]

Skärmklipp.GIF

Då den partiella isobarsfärsytan alltid är vinkelrät mot hornbegränsningsytan i varje punkt kan det möjligen bli lättare att intuitivt förställa sig ljudutbredningen för varje godtycklig hornform tom för en wavegiude.

JM

Vid skarpa kanter, så som vid hornets slut, så kan man inte definiera något så som "vinkelrätt mot hornbegränsningsytan". Det bildas därför reflexer där hornet går över i baffeln, eller där hornet slutar, om det är fritt monterat.

[petersteindl]

Bilagan Skärmklipp.GIF finns inte längre

Då den partiella isobarsfärsytan alltid är vinkelrät mot hornbegränsningsytan i varje punkt kan det möjligen bli lättare att intuitivt förställa sig ljudutbredningen för varje godtycklig hornform tom för en wavegiude.

Några överförenklade förklaringar.

High-Fidelity Uniform-Directivity Loudspeaker
http://www.pispeakers.com/Pi_Speakers_Info.pdf

Loudspeaker Horns - A Crash Course
http://www.fohonline.com/current-issue/ ... ourse.html

Mer detaljer
[ Bild ]
ACOUSTICS. Leo L. Beranek. Source of practical acoustical concepts and theory, with information on microphones, loud-speakers and speaker enclosures, and room acoustics. 491 pp, original published 1954). https://www.amazon.com/Acoustics-Leo-L- ... 088318494X

JM

JM, jag vill dementera vissa saker. Det finns inget horn som ser ut på det sättet som i den bild du visar, annat än då väggarna är raka i ett koniskt horn. Dess akustiska centrum är tänkt att vara där linjerna korsar varandra.


Vill man ändra vinkeln någonstans i det koniska hornet så kan det bli så här:


Det får till följd att då ljudvågen propagerar i hornets början så ligger det akustiska centret i skärningspunkten av de streckade linjerna längst bak i hornet. Därefter då vågen når nästa flare så hoppar det akustiska centret fram till den främre skärningspunkten. Att det skulle ske utan dist av något slag tror jag inte på. Dessutom så bör man beakta hur tvärsnittet ser ut från sidan.

Ingen waveguide som jag känner till satisfierar detta heller om man tittar på tvärsnittet från flera håll. Då måste waveguiden vara helt rotationssymetrisk d v s helt rund.

Nu står visserligen att det att det är ett radialhorn. Då finns möjligheten att man kan få fram ett sådant tvärsnitt från ett håll t.ex. ovanifrån. Men hur ser då ett radialhorn ut i tvärsnitt från sidan.
Så ser ett radialhorn ut sett uppifrån:

Koniskt med en vinkel på +/- 45 grader och som lämpat för hörnplacering om man så vill.
Sett framifrån:


Eller i genomskärning:


Här ser man att från sidan är det inte koniskt utan exponentiellt och då blir det akustiska centret inte samma som från sidan. Hur det påverkar vet jag inte men det kan som jag ser det inte bli en sfärisk vågutbredning. Jag vet att man måste applicera hornekvationerna för exponentiella horn i sådana radialhorn.

Radial horns have two surfaces based on an exponential flare rate, and two straight walls that determine the output pattern. The radial horn exhibits some of the beaming of the exponential horn. Altec sectoral horns were radial horns with vanes placed in the mouth of the horn for the stated purpose of pattern control.

JM, dessutom är det inte så som det står i den bild du visar d v s this is how the plane wave is transformed to a spherical wave without a diffraction slot. Det kan aldrig inträffa det så som det står. Det är i detta avseende som gängse hornteorier fallerar eller kanske snarast uttolkningar av hornteorier. Det kan inte vara så att den partiella isobarsfärsytan alltid är vinkelrät mot hornbegränsningsytan i varje punkt. I den skiss du visar är hornet koniskt från ett håll och under förutsättning att radien på ljudvågen är lika med avståndet till det akustiska centret och detta akustiska centrum inte förflyttar sig så fungerar det, men så är inte fallet i de horn eller waveguides jag sett och aldrig i ett radialhorn. En ljudvåg kan näppeligen transformeras från plan till sfärisk på det sätt som bilden visar utan att ljudvågen deformeras och den deformeras olika beroende på från vilket håll man tittar på tvärsnittet. Det sfäriska hyser jag starka betänkligheter emot. Om det skulle stå ellipsoidiskt istället för sfäriskt i samband med radialhorn så ligger det möjligtvis närmare sanningen men är troligtvis inte helt korrekt ändå. Ett radialhorn är inte rotationssymmetriskt. I texten nedan skall jag försöka förklara problematiken med sfärisk ljudvågsutbredning i horn.

Det finns 2 parametrar att beakta:
1.) Ljudvågen har konstant utbredningshastighet.
2.) Frekvensen på ljudvågen är konstant. Förutsättningen är att hornet/ljudkällan inte färdas med en varierande hastighet i förhållande till lyssnaren. (Exempel på då varierande frekvens uppstår är sirener på polisbil som kör förbi en lyssnare. Det kallas dopplereffekt).

Slutsats 1.) Med dessa parametrar kan man räkna ut att våglängden hos ljudvågen i hornet måste vara konstant. v= ljudvågens hastighet i luft (vid 20 grader C) = våglängd*frekvens. Med v=343 m/s och frekvensen = 1000 Hz blir våglängden = 0,343 meter.

Eftersom hypotesen i det du skriver är att den partiella isobarsfärsytan alltid är vinkelrät mot hornbegränsningsytan i varje punkt så kan man se varje streck/linje/cirkelsegment inuti hornet som en våglängd hos en våg med konstant frekvens. Det kan vara tryckmaxima eller tryckminima, det spelar ingen roll. Det viktiga är att avståndet mellan linjerna d v s cirkelradierna är konstant i exempelvis mitt i hornet d v s On-Axis. Då skall avståndet mellan cirkelradierna vara konstant även vid hornväggarna.

Låt oss för enkelhets roll se det som tryckmaxima. Avståndet mellan linjerna/cirkelsegmenten skall då vara konstant i hornet oavsett om man är mitt i hornet på On-Axis eller vid hornets vägg. Med ovanstående axiom med konstant hastighet och konstant frekvens och därmed konstant våglängd och avståndet mellan linjerna/cirkelsegmenten representerar en våglängd så kan man jämföra avståndet mellan linjerna på olika ställen och var man än är skall avståndet alltid vara konstant. I halsen är det inritat en plan ljudvåg. Senare i hornet är ljudvågen sfärisk med en radie som varierar linjärt med vågens utbredning.

Då kan jag säga att i transitionsområdet så kan inte radien variera linjärt med vågens utbredning såsom din hypotes säger. Det är inte samma avstånd mellan linjerna On-Axis som mellan linjerna på hornets väggar. Men eftersom det måste vara samma avstånd mellan linjerna så måste hypotesen vara felaktig. Något händer i transitionsområdet i skissen som hypotesen inte uppfyller.

Jag kan även säga att alla horn med krökta väggar, vilket alla horn i princip har, uppfyller inte hypotesen. Det kan man enkelt se i skisser.

Låt säga att man i din skiss skulle ritat in en plan baffel längst ut samt ritat in nästa cirkel. Då kan man lätt se att även vid hornets mun d v s i hornets slut så blir det stora problem. Detta har paa redan tagit upp ser jag.

Om man t.ex. tar ett Trac-Trix horn så är det beräknat för en konstant radie genom hela hornet, till skillnad från din skiss som har varierande radie. I början av Trac-Trix så är den konturen lika med ett exponentiellt horn men avslutningen ser helt annorlunda ut och inget av hornen fungerar enligt den hypotes som du satt upp.

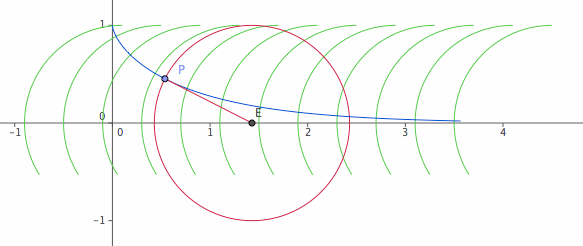
tractrix_orth_circ.png (12.7 KiB) Visad 2390 gånger

Här kan man se att om man följer cirklarnas skärning på X-axeln så är avståndet mellan cirklarnas skärningspunkter mot X-axeln (grön färg mot grå färg) konstant. Om man istället följer cirklarna längs med den blå hornkonturen så ser man att skärningen mellan den blå konturen och cirklarna i grönt inte har konstant avstånd mellan varandra och inte heller samma avstånd som mellan cirklarnas skärningspunkt och X-axeln d v s On-Axis. Men avstånden måste vara lika eftersom frekvensen inte ändras och inte heller hastigheten och därmed inte våglängden. Nånstans är det ett uppenbart fel i hornteorier, i samtliga, eller i vissa, eller i antaganden eller tolkningar gällande hornteorier. Man kan också se att det akustiska centret flyttar sig med ljudvågens fortplantning i hornet. Men vid munnen funkar inte denna princip. Det kan inte vara en helt sfärisk ljudutbredning. Det blir någon form av distorderad ljudvåg i övergångsområdena i hals och i mun.

Vad är då skillnaden mellan en varierande radie och en konstant radie? Jo om man tänker sig att man tar en passare och ställer in radien 5 cm, behåller denna radie konstant, och ritar en cirkel med origo i cirkelns centrum och bibehåller radien då man ritar en mängd cirklar, fast man förskjuter cirklarnas origo längs en rak linje och exempelvis exakt 1 cm mellan varje origo. Då kan man t.ex. rita ut 20 cirklar med respektive origos längs en linje. Det blir som 20 parallellförskjutna cirklar med radien = 5 cm. Se i bilden ovan. Sedan ritas hornet in där väggarna från hals till mun är vinkelräta mot cirkelsektorerna. Därefter kan man mäta om avståndet är konstant mellan cirkelsektorerna vid hornväggarna. Prova så kommer ni se att villkoren för ljudvågor inte kan satisfieras då man närmar sig munnen. Det rör sig om stora skillnader. Ritar man upp alla dessa cirklar så ser man att det akustiska centret inte är konstant på samma plats utan förflyttar sig med cirkelsektorns förflyttning. I en förenklad värld skulle man kunna säga att i slutet av hornet hamnar det akustiska centret i höjd med hornets avslutning d v s mitt i hornets mun. Men så blir det inte med något horn och det är ingen liten skillnad gentemot verkligheten.

Om man istället varierar radien på cirklarna med 1 cm så kan man rita cirklar där alla cirklar har gemensamt origo och då kan man börja med radien 5 cm och sedan rita större cirklar d v s med radierna 6, 7, 8, 9, 10, 11, 12, 13, 14 osv till 25 cm. Då har man 20 cirklar med avståndet 1 cm mellan varje cirkelsektor. Ritar man upp alla dessa cirklar så ser man att det akustiska centret är konstant på samma plats oavsett radie på cirkeln. Vi har nu ritat en punktkälla som inte förflyttar sig.

Nu kan man dela in cirklarna med 2 axlar som utgör ett koordinatsystem med axlarnas skärningspunkt i cirklarnas origo. X och Y, d v s Ett vanligt koordinatsystem. Då fås 4 cirkelsektorer. Om vi nu antar att X-axeln och Y-axeln är plana och raka väggar så kommer ljudvågens utbredning alltid att vara vinkelrät mot dessa väggar som bildar ett hörn med ljudkällan i hörnet. Avståndet mellan cirklarna är identiskt på varje linje som går genom origo d v s genom hörnet. Man kan nu rita in ett koniskt horn med raka linjer genom origo med mindre vinkel än +/- 45 grader och det följer samma princip.

MEN, om väggarna istället kröks med någon form av kurvatur skilt från rät linje så fallerar ovanstående hypotes gällande ljudutbredningen i varje segment i horn.



Om man nu tittar på radien på den sfäriska vågen utanför hornmunnen så ser man att dess längd ger ett akustiskt centrum beläget en bit in i hornet någonstans. Tippar att det är tangenten till vinkeln i munnen som bestämmer radien för den våg som kommer ut ur hornet. Då kan man se skärningspunkten mellan tangenten och On-Axis som akustiskt centrum för vågen ut ur hornet. Men det akustiska centret som vågen har innan den nått fram till skärningspunkten vet jag inget om men den bör ligga längre in i hornet.

Ljudutbredning i luften strax utanför hornets mun måsta ha ett akustiskt centrum längst fram i munnen om ljudet skall satisfiera en punktkällas utbredning med varierande radie och sfärisk vågfront. Men så kan det inte heller bli i detta fall där hornväggarna är krökta och hornet inte är oändligt långt.

Där problemen är som störst är i hornhalsen d v s hornets början och i hornmunnen d v s hornets slut. Där uppstår konstiga fenomen med resonanser och stående vågor som följd. Jag vet också att strax utanför hornets mun så är inte den akustiska impedansen konstant vid varje tvärsnitt mot hornmynningen. Det är just detta fenomen man kan använda sig av i waveguides då man vill forma ljudutbredningen. Dock bör man beakta att ljudvågsfronten inte riktigt ser ut som man först kan tro.

Ett litet runt membran på en stor plan yta t.ex. en vägg ger en vågfront som är en halvsfär. Vinklar man den plana fronten runtom membranet ändras vinkeln från +/- 90 grader till att bli spetsigare t.ex. +/- 45 grader och då har man ett cylindriskt horn. Gör man det fyrkantigt så kan man få ett radialhorn. Med +/-45 grader kan man placera radialhornet i hörn. Gör man den dessutom osymmetrisk med exponentiell form på den vertikala ledden så får man ett traditionellt radialhorn som man kan sätta in i hörnet. Men det finns ytterligare stora svårigheter om man inte vill få destruktiv interferens från hörnets väggar. Det är då en kombination av radialhorn, waveguide och linjärmodifierad trac-trix kanske kan lösa de problem som jag och lilltroll försöker/ämnar lösa.

Med vänlig hälsning
Peter

[JM]

Skärmklipp.GIF

Då den partiella isobarsfärsytan alltid är vinkelrät mot hornbegränsningsytan i varje punkt kan det möjligen bli lättare att intuitivt förställa sig ljudutbredningen för varje godtycklig hornform tom för en wavegiude.

JM

Vid skarpa kanter, så som vid hornets slut, så kan man inte definiera något så som "vinkelrätt mot hornbegränsningsytan". Det bildas därför reflexer där hornet går över i baffeln, eller där hornet slutar, om det är fritt monterat.

Håller med dig paa. Skarpa kanter skapar problem o bör undvikas.
Kontrollerade kanter som i hornet i JBLs K2 kan användas till att sprida ljudet.



JM

[JM]

Geddes huvudsakligen koniska-cylindriska horn/waveguide med mjukare flare distalt enligt patentansökan och nertill hornet i produkten Summa.





Några jämförelser mellan waveguide o horn. Notera att waveguiden från 1993 ger rätt risig tonkurva. Dvs det finns faktorer som har betydelse för en optimal waveguide.







JM

[JM]

Seas 27TDFC utan waveguide

hornconversion-flat-fr.gif (12.77 KiB) Visad 2347 gånger

Waveguide loaded Seas 27TDFC

hornconversion2-horn-fr.gif (12.91 KiB) Visad 2347 gånger

Horn conversion with a 3.3 uF series cap

hornconversion-horn-fr-3.3uf.gif (11.41 KiB) Visad 2347 gånger

http://www.zaphaudio.com/hornconversion.html

En waveguide kräver uppenbarligen lite tonkurvejustering.

JM

[rajapruk]

Med +/-45 grader kan man placera radialhornet i hörn. Gör man den dessutom osymmetrisk med exponentiell form på den vertikala ledden så får man ett traditionellt radialhorn som man kan sätta in i hörnet. Men det finns ytterligare stora svårigheter om man inte vill få destruktiv interferens från hörnets väggar. Det är då en kombination av radialhorn, waveguide och linjärmodifierad trac-trix kanske kan lösa de problem som jag och lilltroll försöker/ämnar lösa.

Skulle dämpning runt hornets ytterkant kunna hjälpa i hörnscenariot? Det har jag funderat på, och sett nämnas någonstans. Alltså att dämpa bort diffraktionerna som blir på ytterkanten.
Kanske i kombination med väl vald dämpning på vägg?

Hörnets problem, kan man dela in det i olika problem för olika frekvenser så att säga?
Vid vilken frekvens ungefär övergår hörnet från att vara konstruktivt till destruktivt, om du fattar vad jag menar?
För i låga frekvenser blir väl hörnet som ett förstärkande horn, i någon mening konstruktivt.

Jag kommer själv lattja lite med hörnplacering framöver, därav dessa frågor. Jag har ett biradialt 60x40 någonting horn som jag tänker ha vertikalt stående, som spelar ner till 650Hz (48db/oct akustisk LR vid 650Hz). Sedan en 15" woofer under. Woofern har inte börjat beama där (650hz), om jag minns rätt.
Några tips för att få detta att funka ok i hörn? Dömt att misslyckas?

Med min ringa kuskap i ämnet, så känns det som en vacker tanke med ett horn som sprider 45grader ur hörnet, tillsammans med en woofer som får hornladdning gratis av rummet, som också sprider 45 grader. Väldigt lik spridning i alla register blir det ju då, the holy grail

Något annat problem än interferenser som kan bli av hörnet? Att man triggar rummet resonanser maximalt är väl en grej (även om jag funderar på att betrakta det som positivt).

[JM]

Några tips för att få detta att funka ok i hörn? Dömt att misslyckas?

Med min ringa kuskap i ämnet, så känns det som en vacker tanke med ett horn som sprider 45grader ur hörnet, tillsammans med en woofer som får hornladdning gratis av rummet, som också sprider 45 grader. Väldigt lik spridning i alla register blir det ju då, the holy grail

Något annat problem än interferenser som kan bli av hörnet? Att man triggar rummet resonanser maximalt är väl en grej (även om jag funderar på att betrakta det som positivt).

Problemet med hörnplacering av allt utom subwoofers är att högtalare är rundstrålande under ca 800 Hz dvs du får ett tonkurvelyft i detta område. Dessutom är det svårt att undvika tidiga reflexer från laterala väggen som ger sämre direktljud o stereobild. Du kommer få svårt att uppfylla LEDE-principen och efterföljaren RFZ (Reflection Free Zone). Du kommer sakna reflexer som kommer efter ca 20 ms dvs mycket sämre ljud.

JM

[rajapruk]

Några tips för att få detta att funka ok i hörn? Dömt att misslyckas?

Med min ringa kuskap i ämnet, så känns det som en vacker tanke med ett horn som sprider 45grader ur hörnet, tillsammans med en woofer som får hornladdning gratis av rummet, som också sprider 45 grader. Väldigt lik spridning i alla register blir det ju då, the holy grail

Något annat problem än interferenser som kan bli av hörnet? Att man triggar rummet resonanser maximalt är väl en grej (även om jag funderar på att betrakta det som positivt).

Problemet med hörnplacering av allt utom subwoofers är att högtalare är rundstrålande under ca 800 Hz dvs du får ett tonkurvelyft i detta område. Dessutom är det svårt att undvika tidiga reflexer från laterala väggen som ger sämre direktljud o stereobild. Du kommer få svårt att uppfylla LEDE-principen och efterföljaren RFZ (Reflection Free Zone). Du kommer sakna reflexer som kommer efter ca 20 ms dvs mycket sämre ljud.

JM

Jag tror du drar generaliserande slutsatser här som inte stämmer på min setup.

Tonkurvelyft är inget problem då jag kör aktivt med dsp, så det kan jag justera in efter smak.

Laterala reflexen tror jag inte kommer bli för tidig faktiskt i mitt rum, det är lång gångväg till sidor, samt öppen planlösning bakåt. Jag har helt ok reflexer i tid tycker jag. Kunde varit en Haas-kick iofs på 30ms, det saknar jag. Men det känns som lite överkurs.

Vad som händer med reflexer från golv och tak är en annan femma, när jag får större vertikal spridning. Det blir spänannde att testa. Jag har alltid inbillat mig att just dessa reflexer är något mindre farliga (tidigt). Att hörselsinnet kan avkoda bort dem pga att de når bägge öronen samtidigt, eller nått!

[rajapruk]

Bumpar dessa nedanstående frågor, om Peter Steindl har missat dem.
Men det kanske tangerar företagshemligheter?

Med +/-45 grader kan man placera radialhornet i hörn. Gör man den dessutom osymmetrisk med exponentiell form på den vertikala ledden så får man ett traditionellt radialhorn som man kan sätta in i hörnet. Men det finns ytterligare stora svårigheter om man inte vill få destruktiv interferens från hörnets väggar. Det är då en kombination av radialhorn, waveguide och linjärmodifierad trac-trix kanske kan lösa de problem som jag och lilltroll försöker/ämnar lösa.

Skulle dämpning runt hornets ytterkant kunna hjälpa i hörnscenariot? Det har jag funderat på, och sett nämnas någonstans. Alltså att dämpa bort diffraktionerna som blir på ytterkanten.
Kanske i kombination med väl vald dämpning på vägg?

Hörnets problem, kan man dela in det i olika problem för olika frekvenser så att säga?
Vid vilken frekvens ungefär övergår hörnet från att vara konstruktivt till destruktivt, om du fattar vad jag menar?
För i låga frekvenser blir väl hörnet som ett förstärkande horn, i någon mening konstruktivt.

Jag kommer själv lattja lite med hörnplacering framöver, därav dessa frågor. Jag har ett biradialt 60x40 någonting horn som jag tänker ha vertikalt stående, som spelar ner till 650Hz (48db/oct akustisk LR vid 650Hz). Sedan en 15" woofer under. Woofern har inte börjat beama där (650hz), om jag minns rätt.
Några tips för att få detta att funka ok i hörn? Dömt att misslyckas?

Med min ringa kuskap i ämnet, så känns det som en vacker tanke med ett horn som sprider 45grader ur hörnet, tillsammans med en woofer som får hornladdning gratis av rummet, som också sprider 45 grader. Väldigt lik spridning i alla register blir det ju då, the holy grail

Något annat problem än interferenser som kan bli av hörnet? Att man triggar rummet resonanser maximalt är väl en grej (även om jag funderar på att betrakta det som positivt).

[petersteindl]

Sorry, jag glömde denna tråd och det har kommit lite annat emellan. Jag skall försöka svara så gott jag kan.

Skulle dämpning runt hornets ytterkant kunna hjälpa i hörnscenariot? Det har jag funderat på, och sett nämnas någonstans. Alltså att dämpa bort diffraktionerna som blir på ytterkanten.
Kanske i kombination med väl vald dämpning på vägg?

Är det ett radialhorn/Waveguide och hornet ligger tätt mot väggar i hörnet så behövs ingen dämpning under förutsättning att dimensioneringen är anpassad för hörn. Värre blir det vertikalt sett. Då kanske man kan vinna något med dämpmaterial längst ute vid kanten, men jag är inte förtjust i dämpning.

1.) Hörnets problem, kan man dela in det i olika problem för olika frekvenser så att säga?
2.) Vid vilken frekvens ungefär övergår hörnet från att vara konstruktivt till destruktivt, om du fattar vad jag menar?
3.) För i låga frekvenser blir väl hörnet som ett förstärkande horn, i någon mening konstruktivt.

1.) Man kan definitivt dela in det i olika frekvensområden där man gör optimal lösning för varje område för sig och man kan hoppas att det gemensamma slutresultatet också blir optimalt.
2.) Antagande: Direktljud har nivån 0 dB och reflexen likaså. Konstruktiv interferens dem emellan ger max +6dB då fasskillnaden mellan direktljud och reflex är nära noll grader. Vid -180 grader dem emellan är de i motfas och total utsläckning sker. vid 90 graders fasdifferens adderar de till +3dB. Vid viss vinkel påverkar inte reflexen och då blir summan 0 dB. Man kan se denna punkt som skiljepunkten mellan positiv/konstruktiv och destruktiv interferens. Men 6 dB skillnad är betydligt mer än vad jag accepterar. Men om reflexen är betydligt svagare än direktljudet så är man med i matchen igen. Det kan man räkna in i waveguiden och möjligtvis kan man förbättra med dämpning om det behövs.
3.) Vid låga frekvenser blir våglängden längre och fasdifferensen blir liten mellan direktljud och reflex vilket innebär summation i praktiken med ungefär 5-6 dB. I hörn mot golv blir det dock inte bara 1 reflex + direktljud utan det blir 3 fördubblingar på direktljudet vilket medför upp till 18 dB summation. Då blir det betydligt känsligare för att uppnå rak frekvensgång. Man kan lätt förlora 18 dB d v s hamna på noll. Det brukar ske nånstans mellan 120-240 Hz. Med tanke på detta och om man skulle rekommendera konsument som skall ha godtycklig basmodul placerad godtyckligt i rummet så skulle jag begränsa frekvensgången i basen till 80 Hz vilket THX eller Dolby har valt i sina standarder och jag förstår dem. Men om man verkligen filar på en specialsub och lyckas få upp den till ung 2 kHz i hörn mot golv utan destruktiv interferens så ser saken betydlig ljusare ut.

Jag kommer själv lattja lite med hörnplacering framöver, därav dessa frågor. Jag har ett biradialt 60x40 någonting horn som jag tänker ha vertikalt stående, som spelar ner till 650Hz (48db/oct akustisk LR vid 650Hz). Sedan en 15" woofer under. Woofern har inte börjat beama där (650hz), om jag minns rätt.
Några tips för att få detta att funka ok i hörn? Dömt att misslyckas?

Har du ett radialhorn som du vill placera tätt in i hörn så skulle jag förorda att, om radialhornet är +/- 45 grader i ena ledden, placera hornet i hörnet så att hornet i sig är början på hörnet och att väggarna blir en naturlig förlängning av hornet ut i rummet.

Att få rak frekvensgång från djup bas till över 650 Hz från en 15" woofer i hörn är inte lätt. Det kräver verkligen extraordinära tilltag. Du måste även tänka på volymen i lådan. Jag har egentligen inget tips för en 15" bas. Jag kör själv med 10" i hörn vilket motsvarar 8*10" basar i frifält. Jag använder ju även 2 st 10" basar som center och placerade vid vägg mot golv. En 10" bas i hörn/golv kommer att ha ungefär 103 dB känslighet vid 2,8 volt.

Med min ringa kuskap i ämnet, så känns det som en vacker tanke med ett horn som sprider 45grader ur hörnet, tillsammans med en woofer som får hornladdning gratis av rummet, som också sprider 45 grader. Väldigt lik spridning i alla register blir det ju då, the holy grail

Spridningen i mellanregister och diskant skall vara +/- 45 grader i horisontalplan från hörn och samma blir det i basen. Det är definitivt inte lätt att uppnå. Blir det beaming/lobningseffekt på grund av destruktiva interferens så har man förstört spridningsmönstret. Lyckas man så tror jag att det blir the holy grail.

Något annat problem än interferenser som kan bli av hörnet? Att man triggar rummet resonanser maximalt är väl en grej (även om jag funderar på att betrakta det som positivt).

Lyckas man tämja problemen med destruktiv interferens så kan man hälla upp ett glas Barolo och njuta av musik och vinet. Efter ett tag tar man itu med rumsresonanser. Men från början måste man bestämma vilka 2 hörn man tänker använda sig av. Gemensam långvägg eller gemensam kortvägg? Har man center så tänker i alla fall jag ha hörnhornen på gemensam långvägg d v s det blir brett mellan höger och vänster hörnhögtalare. Utan center skulle jag prova båda dera, men det beror lite på rummets mått. Personligen tror jag att man med hörnplacering och wave-guides behöver frekvenskompensera en del på högtalarens direktljud vilket ju ungefär blir dess utstrålade energi om man dimensionerar för det.

Med vänlig hälsning
Peter

[rajapruk]

Tack! Mycket att fundera på
Att största problemet kommer bli där någonstans mellan 100-300Hz har jag misstänkt länge. Så var det när jag körde hörnplacering innan med JBL 4429.
Synd att det är ett så viktigt register.
Enda vägen fram för min del som jag ser nu blir nog att laborera med dämpning, och att kunna få woofen så långt i i hörnet som möjligt.
Hade varit grymt kul att få bjuda hem dig på det där glaset Barolo någon gång i framtiden, serverad i en "holy grail"-kalk

[rajapruk]

Nu blev jag sugen på att prova att ha min 15" woofer i en trekantig låda med minimal bredd på sidorna, bara för att testa hur det blir. Med motsvarande trekant dämpning ovanpå, hela vägen upp till tak. Hornet infällt i denna dämpning. (Jag tror mitt horn+driver blir för djupt för att kunna ansluta perfekt till sidoväggarna).

En baffelvägg med 45-grader kortslutet hörn med woofern inne i hade inte varit fel heller, gissar jag. Där vill jag nog hamna på sikt.