JM skrev:Half Elevation Vector Space
Something to make note of when using Dolby Atmos is that out of the box for both the object-bed and the channel-bed there is a limited vector space, specifically there is from the “floor” to the “ceiling” since this is originally designed for theater based mixing. That means that when translated to a virtual setting (expectations we would have for spatial audio mixing) we face our first observed limitation, we are missing 50% of the virtual mixing space.https://research.mach1.tech/posts/obser ... al-mixing/JM
Jag är inte imponerad av denna internetsidas förklaringstext.
Vad är det egentligen det som står?
Vad är betydelsen av det de skriver?
Vector Space, även kallad Linear Space är ett vektorrum. Då kan man gå in på definitionen av ett vektorrum:
Wiki skrev:VECTOR SPACE
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called vectors, may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space.
Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear equations.
Vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. This means that, for two vector spaces over a given field and with the same dimension, the properties that depend only on the vector-space structure are exactly the same (technically the vector spaces are isomorphic).
Redan här tror jag deras förklaringsmodell faller.
Vad är definitionen på Half Elevation?
Sedan används uttryck som Channel-bed och Object-bed.
Vad är definitionen på Channel-bed och Object-bed?
Googlar man på Channel-bed så kommer man till olika sängar eller floder,

vilket är såsom jag själv skulle definiera begreppet.
Det finns även fler konstigheter som inte ges någon definition eller förklaring.
Går man in på vektorer så hamnar man i en helt annan värld med helt andra förklaringsmodeller och till och med helt andra matematiska beräkningar/operatorer, d v s addition och multiplikation sker enligt helt annan modell med vektorer eller vektorvärda funktioner än vad man annars är van vid.
Exempel på vanliga operatorer: Tag två tal.
A = 3.
B = 9.
A + B = 12.
A-B = -6.
B-A = +6
A*B = B*A = 27.
A/B = 1/3.
B/A = 3.
Tal utgör det man matematiskt kallar 'Skalär'. De kan ses som en magnitud.
Ibland kallas de för amplitud, exempelvis om man mäter spänningar inom elektroniken. Då blir enheten Volt.
Går man in i vektoralgebran, så är det helt annan beräkning av operatorer. Då kommer riktning med i beräkningen.
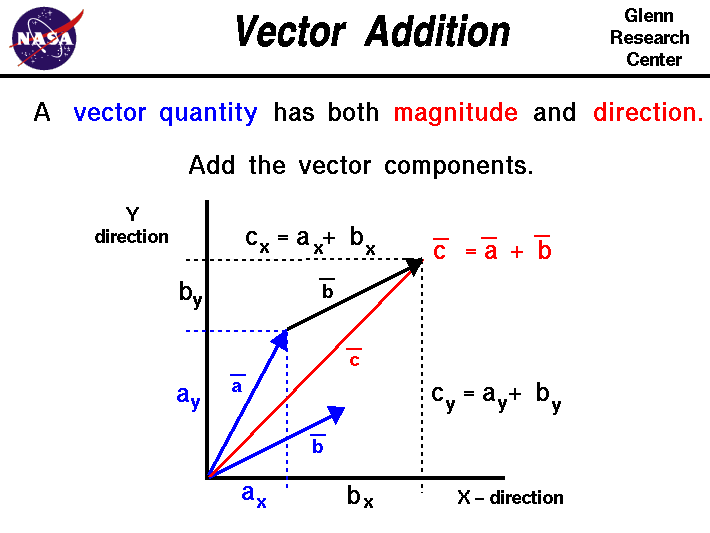
De flesta känner igen det här, men konsekvensen av att använda vektoroperatorer och vad det egentligen innebär och hur man applicerar det inom akustik eller på hörseln som sensoriskt system är tämligen okänt för de absolut flesta.
En annan viktig sak är det man kallar parallellförflyttningsprincipen gällande vektorer. Skilda Vektorer kan vara placerade var som helst i rummet men ändå adderas.
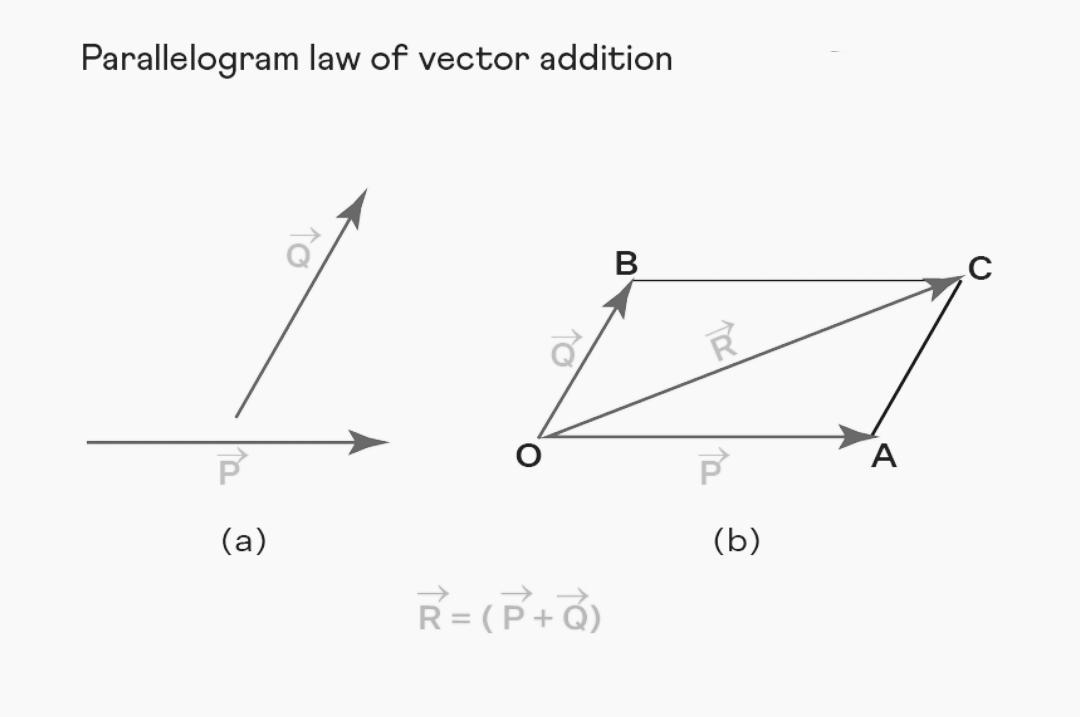
Det kan vara flera vektorer. Additionen sker enligt Triangle Law.
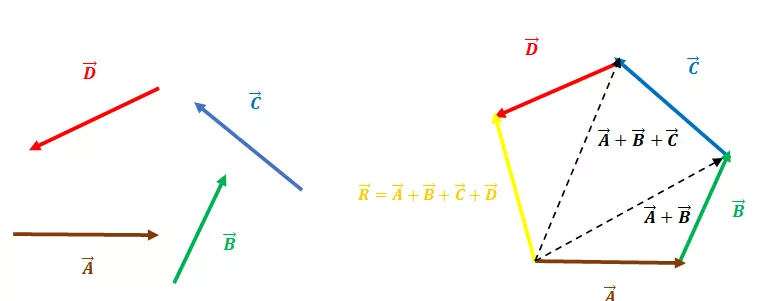
Om detta skall kunna appliceras akustiskt så måste man förstå innebörden. Först måste man bestämma vilken akustisk Storhet/parameter som man egentligen talar om och vill uttrycka?
Tryck och även Ljudtryck är skalära storheter och inte vektorstorheter.
Går man in på Grad, d v s Gradienten, så måste man förstå vad det är för något. Gradienten är en matematisk operator som ett hjälpmedel vid beräkningar.
Har man 2 olika ljudtryck, exempelvis 9 och 3, i 2 olika punkter, t.ex. i punkt A och respektive i punkt B, så blir tryckdifferensen mellan punkterna = 6.
Gradienten är i detta exempel en riktning mellan punkt A och punkt B och längden på vektorn är = 6 som är vektorns magnitud. Skalan kan vi än så länge bortse ifrån. Enheten kan vara Pascal eller dB. Pascal är absoluttryck, dB är logaritmiskt.
Denna tryckgradient är allt annat än det man egentligen vill åstadkomma, inom akustik och om möjligt perception, genom att gå in i vektoralgebrans värld.
Det närmaste man kommer med tryckgradienter är trycket på ena trumhinnan och trycket på andra trumhinnan. Däremellan finns tryckskillnader som kan uttryckas med Gradient som matematisk operator. Då blir riktningen alltid riktningen mellan trumhinnorna och magnituden = vektorns längd, d v s exakt det som framstår vid lyssning med hörlurar. Ljudet är i huvudet mellan trumhinnorna. Då måste det till helt andra ingredienser för att någon extern lokalisation av så kallade "
fantomljudkällor" skall kunna ske. Då kommer man in på vektorfält i vektorrummet/linjära rummet.
Jag, tillsammans med lilltrolls beräkningar och simuleringar har lösningar på detta dilemma, att "externalize" projicering av ljudkällor/ljudobjekt med akustiska vektorer där även tid och fas ingår från vågekvationen i respektive vektor som summeras, men det tänker jag än så länge inte redogöra för, men det är tänkt att komma i Peter Steindl?-tråden, då tiden är mogen.
Från ditt ovanstående inlägg med länk till Innenhof Studio, så står följande att läsa.
Innenhof Studio skrev:In addition, the technology allows theoretically, an unlimited number of audio tracks. In contrast to the purely channel-based surround formats, vector-based metadata for moving objects can be included in the data stream. Then their coordinates are calculated by the receiver relative to the respective measured loudspeaker line-up.
I det här fallet är "the reciever" inte lyssnaren. Men lyssnaren måste komma in i ekvationen om det skall fungera med vektoralgebra och perception.
Det jag reagerar på är: ökar man mängden kanaler och högtalare, så fjärmar man sig vektorernas värld och återger till slut enkom skalära tryck, d v s man går från vektorer till bitmapping.
Slutligen: Jag vill inte förringa deras respektive arbeten, men att använda begreppet vektor i samband med akustik och perception tarvar sin man/kunskap. Jag har ännu inte sett någon text som jag finner ok, gällande detta.
Men vi hör faktiskt riktning. Det medför vissa axiom. Ett av dessa axiom är att hörseln är ett mätinstrument som detekterar någon form av vektorer.
Inom Audio: Ingen frekvenskurva, ingen distorsionskurva, ingen vattenfallskurva och ingen faskurva samt ingen grupplöptid eller någon kurva i tidsdomän innefattar någon som helst vektor. Vektoralgebra används inte inom ljud och perception, men jag har faktiskt börjat göra detta, gällande stereo och lokalisation av ljudobjekt.
MvH
Peter
VD Bremen Production AB + Ortho-Reality AB; Grundare av Ljudbutiken AB; Fd import av hifi; Konstruktör av LICENCE No1 D/A, Bremen No1 D/A, Forsell D/A, SMS FrameSound, Bremen 3D8 m.fl.


