Har du "lyssnat på" Chord M-scaler?

[Morello]

Det där med att flippa mellan de olika uppsamplingarna och bypass-läget inför en osäkerhet vad det är man egentligen jämför, släpper bypass-läget igenom en helt opåverkad signal och varför har de olika uppsamplingarna olika typer av dither (om det nu är så)?

Ett bättre blindtest vore nog att jämföra M Scaler inklusive en bra DAC av samma fabrikat (för att säkerställa att M Scaler gör största möjliga nytta) mot en annan erkänt bra DAC med likvärdig intern uppsampling, koppla dessa två till ett och samma försteg till vardera ingång som relativt snabbt går att välja mellan, samt att dessa är noga volymanpassade.

Det vore intressant att få veta hur M Scaler/Chord DAC skulle stå sig mot exempelvis ett monster som Linn Klimax DSM med Linns egna Organik DAC, men även mot andra DAC-lösningar.

Hur är Linns dacar uppbyggda? FPGA som Chord?

Håller Linn på med upsampling, eller är det bara långa filter de pular med?

Alla (med ytterligt få undantag) DA-omvandlare har översampling; typiskt med en faktor åtta eller sexton. Det är en förutsättning för att kunna implementera ett analogt rekonstruktionsfilter.

[goat76]

Nu leder svarsalternativet "Nej, och är inte intresserad av att göra det" med 14 röster över "Nej, men är nyfiken" på 13.

Nästan lika många - av de som svarat - som är nyfikna som de som inte är intresserade.
Dock vet jag inte om inte intresserad är att likställa med inte nyfiken.

Det vet säkert någon hur det ligger till med.

Jag blir ändå förvånad av de som inte ens är intresserade att lyssna, för även om jag inte är mer intresserad av att lyssna på just en M-scaler över andra liknande produkter så finner jag det ändå intressant ur ett ur ljudintresse-perspektiv.

[goat76]

Hur är Linns dacar uppbyggda? FPGA som Chord?

Håller Linn på med upsampling, eller är det bara långa filter de pular med?

Alla (med ytterligt få undantag) DA-omvandlare har översampling; typiskt med en faktor åtta eller sexton. Det är en förutsättning för att kunna implementera ett analogt rekonstruktionsfilter.

De flesta tillverkare ser väl dock fördelar i så korta signalvägar som möjligt, vilket direkt diskvalificerar en extern uppsamplare.

Chord skulle väl hyfsat enkelt kunna implementera den där M-scalern i deras DACar, åtminstone i deras högre produktserier.

[Morello]

Funkar den utan klocka?

Det verkar den göra.
Här har vi för övrigt motstridiga hävdanden från dCS respektive Watts. Den senare menar att externa klockor är en dålig idé. De förra producerar externa klockor, och menar förmodligen att det är en bra idé.

Det beros ju på hur systemet ser ut - har man multipla apparater som av olika orsaker måste arbeta synkront är en extern klocka helt nödvändig. I en musikanläggningen är det förstås inte så, utan klocka, översamplingsfilter och DA bör sitta i samma låda.

[Strmbrg]

"Nej, och är inte intresserad av att göra det" drar ifrån, härligt!

[PerStromgren]

Hur är Linns dacar uppbyggda? FPGA som Chord?

Håller Linn på med upsampling, eller är det bara långa filter de pular med?

Alla (med ytterligt få undantag) DA-omvandlare har översampling; typiskt med en faktor åtta eller sexton. Det är en förutsättning för att kunna implementera ett analogt rekonstruktionsfilter.

Så, vad tusan kan pryl som denna M-scaler göra för nytta, dåra? Jag fattar inte!

[Strmbrg]

Man måste inte fatta. Det kan räcka med att lyssna.
Åtminstone kan man ta det i den här ordningen:
Lyssna, och sedan - om man så vill - försöka fatta.

[I-or]

"Alla fattar ju att trappstegen efter digitalisering inte kan vara bra! Detta måste ju leda till förlust av mikrodetaljer och en mindre grad av rumslighet, svärta och lugn i återgivningen." Herrar Claude Shannon och Harry Nyquist hade dock inte hållit med om detta.

Det känns som att bluddret om att upp-/översampling tillför magiska egenskaper aldrig tar slut. Bl.a. Chord för fram kraftigt missvisande information i sin marknadsföring.

Morello har författat många mycket informativa inlägg ovan som egentligen borde vara tillräckliga för att alla ska förstå hur detta hänger ihop. Man erhåller via översampling och filter med extremt många tappar inte märkbart högre "upplösning", bättre "timing", högre "precision" eller någonting annat i den stilen. Dessutom översamplar alla DAC:ar (utom knasiga NOS-konstruktioner) numer, så att förlägga denna funktionalitet i en extern låda är anmärkningsvärt.

Det man erhåller via översampling är däremot mer ideala filteregenskaper, vilket ger en mer utsträckt frekvensgång i ultraljudsområdet 20-22,05 kHz och mindre risk för vikningsdistorsion (och om man ska vara noggrann, bättre jitterundertryckning). Dessa fördelar är dock praktiskt sett noll eftersom man måste upp i orimliga ljudtrycksnivåer för att en medelålders person ska kunna överskrida hörseltröskeln runt 20 kHz och risken för hörbar vikningsdistorsion är, som beskrivs ovan, försumbar.

Men visst är det bättre att lyssna. Via simulerad upp-/översampling så kan alla som tur är prova på detta själva.

För att demonstrera hur resultatet från översamplingen ser ut och låter lät jag Matlab sampla om en ljudfil med en faktor 8 och ett 1000 tappar* långt extremt högklassigt filter (typisk filterlängd vid översampling är i sammanhanget futtiga, men tillräckliga, några dussin tappar, mest för att man låter övergångsområdet vara relativt bredbandigt). Filen har alltså konverterats från samplingsfrekvensen 44,1 kHz till 352,8 kHz.

Detta är dock principiellt samma sak som en DAC med en översampling om 8 gånger gör internt, så det som skiljer är endast noggrannheten vid implementeringen av tegelstensväggsfiltret, vilket förstås har tillräckligt goda prestanda i en hygglig DAC som det är. Exakt hur det hela fungerar hemma hos lyssnarna kommer att bero på den specifika DAC:ens egenskaper.

I Strmbrgs anda handlar det om välinspelad storskalig symfoniorkestermusik, här Chabriers välkända stycke España - medvetet utvalt för att erbjuda en hel del systemstressande högfrekvens via tamburin, triangel och cymbaler. Notera hur mycket trevligare och mer "analog" den 8x översamplade signalen ser ut i den digitala domänen (notera att tidsaxeln endast innefattar 0,4 ms):

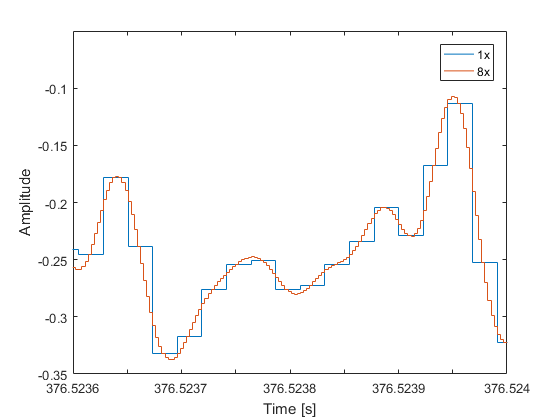
fsx8.png (11.97 KiB) Visad 2128 gånger

Det viktiga är dock hur signalen ser ut och framförallt låter i den analoga domänen efter D/A-omvandling. Lyssna själva med fs = 44,1 kHz respektive 352,8 kHz:

https://www.dropbox.com/scl/fi/izgd1k4zrb664xzkl9crd/Espana-1x.flac?rlkey=apj6v8553n5cx0lr1uu1o4rhh&dl=0

https://www.dropbox.com/scl/fi/6j493llihu0qjlycr9tz8/Espana-8x-1000-taps.flac?rlkey=xwhoq8mxcr32c5w55j33r25r8&dl=0


*Antalet nödvändiga tappar N i ett FIR lågpassfilter kan approximeras som N ≈ 2/3*log[1/(10*δ1*δ2)]*fs/Δf
där δ1 är ripplet i passbandet, δ2 är spärrbandsdämpningen, fs är samplingsfrekvensen och Δf är bandbredden för övergångsområdet

Med ett bra filter om 0,03 dB rippel, 100 dB spärrbandsdämpning och ett övergångsområde om 2000 Hz (alltså t.ex. 21-23 kHz) erhåller man N ≈ 47.

[Strmbrg]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

[sprudel]

Massa bra information(10

Har läst en del av Rob Watts utsagor och försök till förklaringar. Så vitt jag förstår ifrågasatte han räckvidden av av tappar för ett optimalt filter och experimenterade med större antal tappar, mot etablerat ”vetande”, även sitt eget. Det lät bättre i form av tydligare transienter och på den vägen fortsatte han. Rimligtvis kan det vara en orsak till att Strömberg upplever en bättre djupinformation.
Peter Steindl är på samma spår ( och kanske lite till) med den dac han utvecklar med lilltroll, så antagligen är de något på spåren.
En god vän doktorerade på analog och digital signalbehandling, vilket han så småningom omsatte i utvecklandet av hörapparater kopplade till skallbenet. Där hör man!
Enligt honom är inte a/d och d/a inte helt enkelt. Jag kan för lite om det här personligen, så jag väljer lyssning som utvärdering. Chords dacar låter i mina öron bra.
Här är John Atkinsons försök till förklaring (1986) och hans ”förståelse” till varför en extern upsampler som m-scaler är vettig.

https://www.stereophile.com/reference/25/index.html

https://www.stereophile.com/content/cho ... tal-filter

[sprudel]

Här är ett annat försök till förklaring, kanske lite bättre?

https://cdn.abicart.com/shop/1785/art47 ... Howard.pdf

[Almen]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

[Calleberg]

Notera hur mycket trevligare och mer "analog" den 8x översamplade signalen ser ut i den digitala domänen (notera att tidsaxeln endast innefattar 0,4 ms):

Tack som fan, sånna här övningar kan vara rätt kul, och jag uppskattar verkligen tiden du lägger ner.

Men en liten detalj bara...ovanstående citerade textsnutt kan kanske vara förvillade för en del, mig själv inkluderat, eftersom bilden väl ändå visar en ANALOG signal fast före rekonstruktionsfiltret? Efter filtret kommer kurvorna se identiska ut, för säkerhets skull skriver jag att de SER likdana ut, inte att de LÅTER likadant med tanke på vad den här tråden handlar om

Det här vet ju du såklart redan så jag försöker inte manspläijna dig. Men just sånna där bilder brukar användas som bevis av än det ena än det andra av diverse nasare av hi hend produkter så därför tänkte jag dumma ner det lite och eventuellt flytta in det i rätt "domän" så att alla är med på noterna och förstår vad de ser, tror jag

[sprudel]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

Jo, så är det ju om man ska vara strikt. Men inte tusan behöver du heller blindlyssna ditt Bryston mot ett mediokert klass D för att vara övertygad om att skillnad råder. M-scalers låtande har uppfattats av så många att effekten knappast behöver betvivlas.
Att hänföra den till kategorin av Hokus Pokus-lådor, vilket du inte gjort men kanske andra, är nog att dra det för långt. Rob Watts algoritmer i WTA-filtret är antagligen inte kattskit.

[petersteindl]

Notera hur mycket trevligare och mer "analog" den 8x översamplade signalen ser ut i den digitala domänen (notera att tidsaxeln endast innefattar 0,4 ms):

Tack som fan, sånna här övningar kan vara rätt kul, och jag uppskattar verkligen tiden du lägger ner.

Men en liten detalj bara...ovanstående citerade textsnutt kan kanske vara förvillade för en del, mig själv inkluderat, eftersom bilden väl ändå visar en ANALOG signal fast före rekonstruktionsfiltret? Efter filtret kommer kurvorna se identiska ut, för säkerhets skull skriver jag att de SER likdana ut, inte att de LÅTER likadant med tanke på vad den här tråden handlar om

Det här vet ju du såklart redan så jag försöker inte manspläijna dig. Men just sånna där bilder brukar användas som bevis av än det ena än det andra av diverse nasare av hi hend produkter så därför tänkte jag dumma ner det lite och eventuellt flytta in det i rätt "domän" så att alla är med på noterna och förstår vad de ser, tror jag

Njae, det ser för mig ut som Sample and hold signal före analogt filter. Det är först därefter via analogt filter som jag kallar det analog kontinuerlig signal. Före sample and hold ser jag det som diskreta ej tidskontinuerliga samples. Med sample and hold binder man ihop varje sample med varandra genom att hålla nivån konstant och har då en mängd HF-skräp och om jag inte missminner mig, så är det allt skräp ovanför halva samplingsfrekvensen man ser som de fyrkantiga ytorna utanför den analoga signalen under halva samplingsfrekvensen. I den Bremen DAC jag har prototyp av, så har vi 1024 ggr oversampling med 32 bitars upplösning och 15 miljoner taps. Det är mycket viktigt att få ner brusnivån till -200 dB, annars blir det ju bara en ohemuligt stor mängd brus och THD och IM som färgar hela ljudet till oigenkännlighet.

[Strmbrg]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

Två ordningsfrågor:
"Ingen betvivlar att du har upplevt en skillnad"
Hur vet du det? Jag gissar att det finns de som betvivlar det. Hårklyverier månne men nu ska vi väl vara hyfsat sakliga oavsett vad saken gäller

"...den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om."
Tillspetsat kanske, men vilka upplevda skillnader kräver verifiering? Vilka kräver det inte?
Att jag påstår att det är tyst i högerkanal, tex: Behöver det verifieras enligt ovan metod?
Var går gränsen för vad som behöver verifieras?
Jag gissar igen och säger att det såklart inte går att dra den gränsen, men det väcker likafullt tanken om en diffus gränsdragning.

[Almen]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

Jo, så är det ju om man ska vara strikt. Men inte tusan behöver du heller blindlyssna ditt Bryston mot ett mediokert klass D för att vara övertygad om att skillnad råder. M-scalers låtande har uppfattats av så många att effekten knappast behöver betvivlas.

Så kan det vara, men det funkar inte att lämpa över ansvaret på skeptikern. Som JohanL skriver nedan kan det vara en hel massa det beror på (jitter, nivåskillnader, distorsion?), och att då spekulera i overifierade lyssningsintryck ser jag som ogörbart (med hedern i behåll).

Här funkar det så att jag via fjärren stegar runt mellan "by-pass och ett antal uppsamplingssteg upp till den högsta, som beroende på om ursprunget är 44,1 eller 48 kHz, är 705 eller 768 kHz.
Stegningen sker med en enda knapp. "Varvet går runt i en riktning", jag kan förvilla mig själv enkelt genom att själv trycka såpass många gånger att jag tappar kollen på i vilket läge M-scalaren befinner sig i. (Eller låta någon annan välja startläge åt mig - om jag inte litar på min förmåga att tappa räkningen.)

Som HerrD visar ovan, liksom tidigare diskussioner i ämnet, är M Scaler en känd apparat som ändrar signalen i både bypassläge och processat läge. Det som Audio Science Review verkar ha missat är att bypassläget ändrar kraftigt på nivån med nästan 3 dB, men det syns i mätningarna. Det behövs för att nivån på uppsamplingen behöver minskas lika mycket för att undvika digital klippning på grund av uppsamplingsprocessen. Det behöver göras för att du som användare ska uppleva lika stark nivå när du växlar olika lägen. Det kan därtill vara så att det inte är exakt lika höga nivåer heller mellan bypass och de andra lägena vilket gör att du egentligen upplever en nivåskillnad, men det skulle behöva mätas upp och kollas om det är så eller inte, och jag vet inte om någon annan gjort det. Det kan vara så att Chord gjort en mindre bra implementerad volymkontroll för nivåsänkningen i M Scaler, vilket ger distorsion. Om du har en digital källa med två digitala utgångar och kopplar den ena direkt till din DAC och den andra via M Scaler kommer du att höra en enorm skillnad, alltså ännu mer än vad du gör idag när du växlar enbart i M Scaler.

[Calleberg]

Notera hur mycket trevligare och mer "analog" den 8x översamplade signalen ser ut i den digitala domänen (notera att tidsaxeln endast innefattar 0,4 ms):

Tack som fan, sånna här övningar kan vara rätt kul, och jag uppskattar verkligen tiden du lägger ner.

Men en liten detalj bara...ovanstående citerade textsnutt kan kanske vara förvillade för en del, mig själv inkluderat, eftersom bilden väl ändå visar en ANALOG signal fast före rekonstruktionsfiltret? Efter filtret kommer kurvorna se identiska ut, för säkerhets skull skriver jag att de SER likdana ut, inte att de LÅTER likadant med tanke på vad den här tråden handlar om

Det här vet ju du såklart redan så jag försöker inte manspläijna dig. Men just sånna där bilder brukar användas som bevis av än det ena än det andra av diverse nasare av hi hend produkter så därför tänkte jag dumma ner det lite och eventuellt flytta in det i rätt "domän" så att alla är med på noterna och förstår vad de ser, tror jag

Njae, det ser för mig ut som Sample and hold signal före analogt filter. Det är först därefter via analogt filter som jag kallar det analog kontinuerlig signal. Före sample and hold ser jag det som diskreta ej tidskontinuerliga samples. Med sample and hold binder man ihop varje sample med varandra genom att hålla nivån konstant och har då en mängd HF-skräp och om jag inte missminner mig, så är det allt skräp ovanför halva samplingsfrekvensen man ser som de fyrkantiga ytorna utanför den analoga signalen under halva samplingsfrekvensen. I den Bremen DAC jag har prototyp av, så har vi 1024 ggr oversampling med 32 bitars upplösning och 15 miljoner taps. Det är mycket viktigt att få ner brusnivån till -200 dB, annars blir det ju bara en ohemuligt stor mängd brus och THD och IM som färgar hela ljudet till oigenkännlighet.

Okay, en "beror på" grej alltså. När jag skrev "rekonstruktionsfilter" var jag dessutom lite otydlig, jag avser ett analogt sådant som jag antar då även måste ingå i en framtida Bremen DAC Annars skulle isåfall din DAC vara en DDC om man tänker sig att det är filtret som krävs för att det skall ramla över i analog domän Men jag kan köpa det sättet att se på det, det är inte analogt på riktigt förens anrättningen är helt klar, så att säga.

För mig är det så enkelt att en digital signal saknar amplitud annat än vad som krävs för att definiera den som på eller av/0 eller 1.

[I-or]

Notera hur mycket trevligare och mer "analog" den 8x översamplade signalen ser ut i den digitala domänen (notera att tidsaxeln endast innefattar 0,4 ms):

Tack som fan, sånna här övningar kan vara rätt kul, och jag uppskattar verkligen tiden du lägger ner.

Men en liten detalj bara...ovanstående citerade textsnutt kan kanske vara förvillade för en del, mig själv inkluderat, eftersom bilden väl ändå visar en ANALOG signal fast före rekonstruktionsfiltret? Efter filtret kommer kurvorna se identiska ut, för säkerhets skull skriver jag att de SER likdana ut, inte att de LÅTER likadant med tanke på vad den här tråden handlar om

Det här vet ju du såklart redan så jag försöker inte manspläijna dig. Men just sånna där bilder brukar användas som bevis av än det ena än det andra av diverse nasare av hi hend produkter så därför tänkte jag dumma ner det lite och eventuellt flytta in det i rätt "domän" så att alla är med på noterna och förstår vad de ser, tror jag

Hur man väljer att representera digitala signaler handlar mest om tycke och smak. I praktiken handlar det förstås om en serie av diskreta värden separerade av ett konstant tidssteg. Jag tänkte först bara lägga in ett normalt diagram med linje-till-linje-representation av samplen (som jag har gjort många gånger tidigare), men valde trappstegsdiagrammet för att man i marknadsföringen ofta gör på det sättet. Ett sampel är ett sampel oavsett, så frågan blir lite av filosofisk natur.

Hur signalen sedan ser ut i den analoga domänen beror förstås på DAC:ens egenskaper.

[goat76]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

Två ordningsfrågor:
"Ingen betvivlar att du har upplevt en skillnad"
Hur vet du det? Jag gissar att det finns de som betvivlar det. Hårklyverier månne men nu ska vi väl vara hyfsat sakliga oavsett vad saken gäller

Om det är någon läsare av tråden som skulle betvivla det du säger och beskriver angående din upplevelse så skulle det innebära att personen tror att du ljuger, men det är det nog ytterst få som tror om ens någon.

Det vissa läsare däremot möjligtvis är tveksamma till är om de ljudmässiga förbättringarna du upplever verkligen är orsakade av det denna externa uppskalare är tänkt att "bära med till partyt". Den biten är tyvärr svår att bekräfta då det mellan de olika uppskalningslägen som finns drar med sig okännbara variabler, så av den orsaken vore det nog bättre om en lyssningsjämförelse istället skulle göras mot en annan DAC av erkänt god kvalitet (inklusive den uppskalning som sker i denna) och där endast högsta uppskalningsläget används i M-scaler.

"...den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om."
Tillspetsat kanske, men vilka upplevda skillnader kräver verifiering? Vilka kräver det inte?
Att jag påstår att det är tyst i högerkanal, tex: Behöver det verifieras enligt ovan metod?
Var går gränsen för vad som behöver verifieras?
Jag gissar igen och säger att det såklart inte går att dra den gränsen, men det väcker likafullt tanken om en diffus gränsdragning.

Vilka grad av ljudmässiga upplevelser som behöver verifieras varierar nog från lyssnare till lyssnare. Några extremfall av vissa lyssnare kan säkerligen höra saker som verkligen inte finns där bara av "feel good"-känslan av att äga en apparat som anses ha egenskaper utöver det vanliga, medans andra lyssnare kanske inte ens är mottagliga för relativt stora ljudskillnader som faktiskt finns där då personen i fråga kanske fokuserar all sin koncentration på andra aspekter i ljudet.

[Almen]

"Ingen betvivlar att du har upplevt en skillnad"
Hur vet du det? Jag gissar att det finns de som betvivlar det. Hårklyverier månne men nu ska vi väl vara hyfsat sakliga oavsett vad saken gäller

Jag kan försöka förtydliga till en mer formell formulering: "Jag har ingen entydig evidens för att någon betvivlar att du upplevt en skillnad." Anledningen till att jag skrev det lite hårdare var att jag även anser det tillhöra hyfs och god ton att inte ifrågasätta människors subjektiva upplevelser.

På ett liknande sätt kan jag förhålla mig till din utsaga om Chord M-scaler: "Jag har ingen entydig evidens för att M-scalern tekniskt skulle ge de ljudskillnader som du uppger." Och här med brasklappen om nivåmatchade slumpade blindtest.

Epistemologiskt är det en grundpelare i naturalismen: när vi inte har tillräckliga indata måste vi våga säga att vi inte vet och att vi inte kan uttala oss om saken. Det är så naturvetenskapen skall fungera.*

"...den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om."
Tillspetsat kanske, men vilka upplevda skillnader kräver verifiering? Vilka kräver det inte?
Att jag påstår att det är tyst i högerkanal, tex: Behöver det verifieras enligt ovan metod?
Var går gränsen för vad som behöver verifieras?
Jag gissar igen och säger att det såklart inte går att dra den gränsen, men det väcker likafullt tanken om en diffus gränsdragning.

Var och en får så klart dra sina egna gränser. Om någon hävdar att X orsakar cancerform Y och att naturläkemedel Z botar detta, skulle då du tycka att det behövdes lite mer noggranna undersökningar eller accepterar du okritiskt utsagan?

*) "Wovon mann nicht sprechen kann, darüber muss mann schweigen."

[I-or]

Här är ett annat försök till förklaring, kanske lite bättre?

https://cdn.abicart.com/shop/1785/art47 ... Howard.pdf

Keith Howard vänder verkligen ut och in på sig och matematiken bakom digitala filter för att finna något vettigt i Chords produkter. Hans resonemang framstår som ganska märkligt, då han mycket väl känner till att samtliga systemegenskaper definieras av systemets impulssvar eller frekvenssvar. Vi behöver således egentligen inte veta någonting alls om vad som sker under skalet utan det räcker med att utföra en sådan mätning för att kunna avgöra om prestanda är adekvata givet hörselns begränsningar (övre gränsfrekvens, rippel och störningar).

Samtidigt är herr Howard definitivt inte någon dumskalle, speciellt inte när det gäller digitalteknik, så han beskriver bara bakgrunden till tekniken och anför inte att det skulle finnas några hörbara skillnader (vilket han alltid har gjort när han har funnit dem i andra sammanhang).

[I-or]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Jag överlåter åt läsarna av tråden att jämföra de två ljudfilerna på egen hand. Oaktat detta så finns det absolut ingenting i egenskaperna för de olika filtren som rimligen skulle kunna leda till att just ljudsceneriet förändras, då hörselns känslighet är störst här runt sådär 1-10 kHz. I detta frekvensområde blir det definitivt inte annat än fullständigt försumbara skillnader mellan olika filter från några dussin tappar och uppåt.

Möjligen, möjligen skulle en ung person med ovanligt god högfrekvenshörsel kunna höra skillnad på högfrekvensutsträckningen runt 21-22 kHz eller så, men även detta är ganska tveksamt och förutsätter dessutom högre signalnivåer än i majoriteten av klassiska inspelningar. Dock skulle Inte heller detta ge någon påtaglig skillnad för ljudsceneriet. Man bör i sammanhanget känna till att luftabsorptionen vid 20 kHz är så hög att det skiljer sådär 2-5 dB för direktljudet mellan en plats i främre delen av konsertlokalen och mitten av densamma. Ljudsceneriet förändras förstås inte av detta och den som har ekvaliserat sina diskanter till att ha konstant frekvensgång ända upp till 20 kHz har knappast hört några skillnader i det avseendet heller.

När det gäller blindtestning av Chords M-Scaler på egen hand så är det ett problem att växlingen mellan 1x och 2x sker avbrottsfritt, men att växlingen från 4x och uppåt ger ett avbrott (allt enligt ASR:s test), vilket förstås beror på de långa filtren. Detta medför att man kanske omedvetet blir varse var växlingspunkterna ligger och därmed lär sig att identifiera sekvensen.

[sprudel]

Först måste man i så fall kontrollera att dina lyssningsintryck korrelerar med en fysikalisk verklighet. Ingen betvivlar att du har upplevt en skillnad, men den måste verifieras genom nivåmatchning och slumpad blind lyssning så att vi vet vad det är vi pratar om.

Jo, så är det ju om man ska vara strikt. Men inte tusan behöver du heller blindlyssna ditt Bryston mot ett mediokert klass D för att vara övertygad om att skillnad råder. M-scalers låtande har uppfattats av så många att effekten knappast behöver betvivlas.

Så kan det vara, men det funkar inte att lämpa över ansvaret på skeptikern. Som JohanL skriver nedan kan det vara en hel massa det beror på (jitter, nivåskillnader, distorsion?), och att då spekulera i overifierade lyssningsintryck ser jag som ogörbart (med hedern i behåll).

Här funkar det så att jag via fjärren stegar runt mellan "by-pass och ett antal uppsamplingssteg upp till den högsta, som beroende på om ursprunget är 44,1 eller 48 kHz, är 705 eller 768 kHz.
Stegningen sker med en enda knapp. "Varvet går runt i en riktning", jag kan förvilla mig själv enkelt genom att själv trycka såpass många gånger att jag tappar kollen på i vilket läge M-scalaren befinner sig i. (Eller låta någon annan välja startläge åt mig - om jag inte litar på min förmåga att tappa räkningen.)

Som HerrD visar ovan, liksom tidigare diskussioner i ämnet, är M Scaler en känd apparat som ändrar signalen i både bypassläge och processat läge. Det som Audio Science Review verkar ha missat är att bypassläget ändrar kraftigt på nivån med nästan 3 dB, men det syns i mätningarna. Det behövs för att nivån på uppsamplingen behöver minskas lika mycket för att undvika digital klippning på grund av uppsamplingsprocessen. Det behöver göras för att du som användare ska uppleva lika stark nivå när du växlar olika lägen. Det kan därtill vara så att det inte är exakt lika höga nivåer heller mellan bypass och de andra lägena vilket gör att du egentligen upplever en nivåskillnad, men det skulle behöva mätas upp och kollas om det är så eller inte, och jag vet inte om någon annan gjort det. Det kan vara så att Chord gjort en mindre bra implementerad volymkontroll för nivåsänkningen i M Scaler, vilket ger distorsion. Om du har en digital källa med två digitala utgångar och kopplar den ena direkt till din DAC och den andra via M Scaler kommer du att höra en enorm skillnad, alltså ännu mer än vad du gör idag när du växlar enbart i M Scaler.

Men här spekulerar väl Johan angående ljudnivåerna bypass och uppsampling?

[sprudel]

Jag får låna hem en M-scaler och lyssna på den, dels för att höra vad den ger, dels för att utröna ljudnivåskillnader mellan bypass och uppsampling.
Men nu finns det en beg Dave på nätet i Sverige…….

[goat76]

Tack!

Kan du även förklara vad den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras?
Det kanske blir samma effekt i de filer du tillhandahåller. Kan dessvärre inte lyssna på dem annat än via enkla höronpluppar och laptop de närmaste dagarna.

Djup, och storleken på sceneriet som helhet, mer precist uttryckt.

Jag överlåter åt läsarna av tråden att jämföra de två ljudfilerna på egen hand. Oaktat detta så finns det absolut ingenting i egenskaperna för de olika filtren som rimligen skulle kunna leda till att just ljudsceneriet förändras, då hörselns känslighet är störst här runt sådär 1-10 kHz. I detta frekvensområde blir det definitivt inte annat än fullständigt försumbara skillnader mellan olika filter från några dussin tappar och uppåt.

Möjligen, möjligen skulle en ung person med ovanligt god högfrekvenshörsel kunna höra skillnad på högfrekvensutsträckningen runt 21-22 kHz eller så, men även detta är ganska tveksamt och förutsätter dessutom högre signalnivåer än i majoriteten av klassiska inspelningar. Dock skulle Inte heller detta ge någon påtaglig skillnad för ljudsceneriet. Man bör i sammanhanget känna till att luftabsorptionen vid 20 kHz är så hög att det skiljer sådär 2-5 dB för direktljudet mellan en plats i främre delen av konsertlokalen och mitten av densamma. Ljudsceneriet förändras förstås inte av detta och den som har ekvaliserat sina diskanter till att ha konstant frekvensgång ända upp till 20 kHz har knappast hört några skillnader i det avseendet heller.

När det gäller blindtestning av Chords M-Scaler på egen hand så är det ett problem att växlingen mellan 1x och 2x sker avbrottsfritt, men att växlingen från 4x och uppåt ger ett avbrott (allt enligt ASR:s test), vilket förstås beror på de långa filtren. Detta medför att man kanske omedvetet blir varse var växlingspunkterna ligger och därmed lär sig att identifiera sekvensen.

Jag gjorde nyss ett snabbt men inte speciellt omfattande blindtest mellan dina två ljudfiler, och resultatet var faktiskt att jag hörde en skillnad som jag prickade in 7 av 8 gånger. Skillnaden jag upplevde var just en något högre grad av luftighet i den uppsamplade ljudfilen.

[sprudel]

Har inte Svante kikat på Chord Qutest i Molt?

[RogerGustavsson]

Jag får låna hem en M-scaler och lyssna på den, dels för att höra vad den ger, dels för att utröna ljudnivåskillnader mellan bypass och uppsampling.
Men nu finns det en beg Dave på nätet i Sverige…….

Ska den där Dave också ha en extern uppsamplare?

[I-or]

Jag gjorde nyss ett snabbt men inte speciellt omfattande blindtest mellan dina två ljudfiler, och resultatet var faktiskt att jag hörde en skillnad som jag prickade in 7 av 8 gånger. Skillnaden jag upplevde var just en något högre grad av luftighet i den uppsamplade ljudfilen.

Ja, givet det för klassisk musik ovanligt stora högfrekvensinnehållet i ljudfilerna är det inte omöjligt att höra skillnad längst upp i toppoktaven (förutsatt att man drar på ordentligt), men här kommer den specifika DAC:ens egenskaper att vara avgörande. Det räcker med någon tiondels dB i frekvensgångsskillnad för att uppnå hörbarhet. Inspelningen innehåller egentligen nästan ingenting över knappt 21 kHz, för övrigt.

Mitt resonemang ovan utgår egentligen ifrån ett scenario med en inom ramen för antalet tillgängliga tappar psykoakustiskt optimalt utformad filtrering i anknytning till den interna översamplingen, då skillnaderna mot det långa Matlab-filtret blir ytterst små.

Samtidigt skulle jag nog tro att effektstorleken med en vettig DAC är minimal och att skillnaderna inte är mycket att orda om även om detektion är möjlig.

[Almen]

Jo, så är det ju om man ska vara strikt. Men inte tusan behöver du heller blindlyssna ditt Bryston mot ett mediokert klass D för att vara övertygad om att skillnad råder. M-scalers låtande har uppfattats av så många att effekten knappast behöver betvivlas.

Så kan det vara, men det funkar inte att lämpa över ansvaret på skeptikern. Som JohanL skriver nedan kan det vara en hel massa det beror på (jitter, nivåskillnader, distorsion?), och att då spekulera i overifierade lyssningsintryck ser jag som ogörbart (med hedern i behåll).

Som HerrD visar ovan, liksom tidigare diskussioner i ämnet, är M Scaler en känd apparat som ändrar signalen i både bypassläge och processat läge. Det som Audio Science Review verkar ha missat är att bypassläget ändrar kraftigt på nivån med nästan 3 dB, men det syns i mätningarna. Det behövs för att nivån på uppsamplingen behöver minskas lika mycket för att undvika digital klippning på grund av uppsamplingsprocessen. Det behöver göras för att du som användare ska uppleva lika stark nivå när du växlar olika lägen. Det kan därtill vara så att det inte är exakt lika höga nivåer heller mellan bypass och de andra lägena vilket gör att du egentligen upplever en nivåskillnad, men det skulle behöva mätas upp och kollas om det är så eller inte, och jag vet inte om någon annan gjort det. Det kan vara så att Chord gjort en mindre bra implementerad volymkontroll för nivåsänkningen i M Scaler, vilket ger distorsion. Om du har en digital källa med två digitala utgångar och kopplar den ena direkt till din DAC och den andra via M Scaler kommer du att höra en enorm skillnad, alltså ännu mer än vad du gör idag när du växlar enbart i M Scaler.

Men här spekulerar väl Johan angående ljudnivåerna bypass och uppsampling?

Nja, han spekulerar inte i vad "den ökade illusionen av djup i ljudsceneriet orsakas av - när Chord M-Scaler involveras". Johan påpekar bara alla de felkällor som finns när man lyssnar öppet.