Moderator: Redaktörer
Juanth skrev:Mfc är mycket trevliga. Polypropen som eliminerar uppbrytning. De har ett mycket bra beteende.
juanth skrev:Här är en samling av SB Acoustics egna mätningar på diverse av de element de saluför.
Det kan väl passa i den här tråden?
Den nedre är normaliserad.
I-or skrev:Det finns inga material som ens är nära att dämpa ut böjmoder i konen till den grad som är nödvändig för att uppnå den tulipanaros som ett element utan märkbara uppbrytningar och med frekvensen minskande strålande yta skulle kunna utgöra. Detta låter sig helt enkelt inte göras och man bör ställa sig ytterst tveksam till olika uttalanden om att detta är möjligt. Vissa tillverkare har t.o.m. arbetat med s.k. avstämda dämpare i surrounden med viss framgång, men utan att för den skull bli av med problemet.
Jag vill påstå att man ser tydliga membrandistorsionseffekter för alla element som används upp till strax under första uppbrytningsfrekvensen eller högre (vilket gäller för alla fullrange tvåvägshögtalare med normala konmaterial och delningsfrekvenser). Denna distorsion ligger ofta uppåt 1-3 % (THD) vid lite högre ljudtrycksnivåer och är klart hörbar.
I-or skrev:Om man inte kan få till ett litet avstånd relativt våglängden mellan elementen (oftast mycket svårt i praktiken) så är det bättre att överskrida en våglängd, precis som Maarten är inne på ovan. Detta ger den bästa kompromissen för den vertikala spridningen. Även om detta kanske av vissa inte betraktas som vackert så behöver man inte oroa sig för närgränsen, då hörseln accepterar ganska stora skillnader för källpositionerna i höjdled.
Fördelen med koner som är utförda i mindre styva material som t.ex. polypropen är att förlusterna vanligen är relativt höga, vilket minskar ojämnheterna i frekvensgången i uppbrytningsområdet. Dessutom medför uppbrytningarna att spridningen blir högre (konens delytor svänger med olika faslägen, vilket inte ger lika hög riktverkan som en ideal kolv som något överdrivet skickar vågorna rakt framåt när omkretsen är stor relativt våglängden).
Nackdelen är att uppbrytningarna börjar att bli märkbara vid relativt låga frekvenser, runt en oktav under den första böjresonansfrekvensen för konen. Detta leder till omfattande membrandistorsion, då polymerer har olinjära spännings-töjningsegenskaper.
Denna distorsion hamnar även i det för hörseln allra känsligaste området, vilket i kombination med att det handlar om det övre grundtonsområdet leder till överlag otrevliga ljudande egenskaper, men framförallt för kvinnoröster, pianon och bleckblåsinstrument.
Erhöll dock ganska små avvikelser mellan olika vinklar, typ någon cm vid 2 KHz, vilket ju inte innebär några större fasskillnader.
Var innan mätningen något fundersam kring nyttan med VFC då jag funderade ifall vågorna ändå "jämnar ut" sig en bit ifrån, dvs att begreppet kanske är lite förenklat? (Möjligen kanske lite olika beroende på mjuka/hårda koner?) Men vad vet jag? I-or vet dock nog...
Maarten skrev:Schumi: här är mer info kring c-c-avstånd: viewtopic.php?f=3&t=73462&start=780#p2305498
Men det har du ju kommenterat även då, skriver bara för att det är olika aspekter att ta hänsyn till, både vertikala vinklar och DI.
****
En fråga till I-or eller annan kunnig inom vågutbredning i luft ang detta med vågfrontcentrum och 'sfäriska vågor': Jag har läst om dessa begrepp under årens lopp och försökte som nybörjare i det mesta även testa detta men inte med meningsfulla resultat. Då konkluderade jag:Erhöll dock ganska små avvikelser mellan olika vinklar, typ någon cm vid 2 KHz, vilket ju inte innebär några större fasskillnader.
Var innan mätningen något fundersam kring nyttan med VFC då jag funderade ifall vågorna ändå "jämnar ut" sig en bit ifrån, dvs att begreppet kanske är lite förenklat? (Möjligen kanske lite olika beroende på mjuka/hårda koner?) Men vad vet jag? I-or vet dock nog...
Vill även minnas att du I-or skrev att Klippel ger en bättre bild ljudfältet än konventionella mätningar, vilket fick mig att fundera över hur noggrant vanliga mikrofoner/mätmetoder kan mäta sånt här.
Frågor:
Hur långt ifrån behöver man mäta för att en vågrfront ska ha stabiliserat sig?
Är det ett användbart begrepp för element med koner som bryter upp med olika faslägen?
Förutsätter det frifält?
Rille skrev:I-or skriver "konens delytor svänger med olika faslägen, vilket inte ger lika hög riktverkan som en ideal kolv som något överdrivet skickar vågorna rakt framåt när omkretsen är stor relativt våglängden".
Jag har inga problem med den beskrivningen, men jag hade förenklat skrivit att elementet börjar arbeta vågformigt istället för kolvformigt över en för elementet given frekvens och ju längre in mot mitten desto högre frekvens skapas.
Maarten skrev:Frågor:
Hur långt ifrån behöver man mäta för att en vågrfront ska ha stabiliserat sig?
Är det ett användbart begrepp för element med koner som bryter upp med olika faslägen?
Förutsätter det frifält?
schmutziger skrev:Precis, dela högre än vad jag redan gör är inte intressant.
Lilleman har knäckt min laptop så jag är lite fast i att mäta inomhus.
Har lite extra material över så jag ska nog bygga ett par testbafflar med maxxat cc.
Hittade dessa.mätningar jag hade visat i dft tråden
[ Bild ]
[ Bild ]
https://faktiskt.io/phpBB3/download/file.php?id=42867
https://faktiskt.io/phpBB3/download/file.php?id=42866
Dist vid 90dB,
Dist vid 90dB,
Den undre 0-50grader
mätt.mot en projektorduk pga vad lilleman har gjort med min laptop.
Så lite reflektiv närmiljö. Lite kavr o göra men ingen dealbreaker i ljudet för mig iaf.
delPietro skrev:Själv använder jag 1-1,5 meter mikrofonavstånd...
...
Jag vill inte ha membranuppbrytning i delningsområdet. Då man får en dipp eller en topp i frekvensgång så byter fasen tecken och då funkar inte summeringen som tänkt.
...
För att vågfront skall vara ett användbart begrepp så bör den vara homogen, d v s frekvensgången i given riktning bör inte förändras då mikrofonavståndet varierar i den riktningen. Riktningen kan ses som en vektor.
I-or skrev:Detta är ett missförstånd som tyvärr dyker upp ibland och speciellt på detta forum.
Rille skrev:Tack I-or, Peter och Maarten för all tid du/ni lägger på förklaringar och till och med fina pedagogiska bilder. Om det nu inte är ungefär som min förenkling, vilket fenomen gör att man får en halvsfäriskt vågfront i från ett element som är större än våglängden som skapas?
Eller har jag missat något?
Rille skrev:... Eller i allafall en mycket lik form då det är svårt att mäta med måttband, jag borde spänt ett snöre mitt framför elementet som referens eller haft en kartongbit med bågen utritad på och mätt med laser mätare. Det får bli nästa gång jag gör en sån mätövning.
petersteindl skrev:Rille, varför skulle du se en sådan dipp?
Det I-or beskriver är ett fenomen som uppstår vid någon frekvens hos konelement.
Är delningsfrekvensen under dessa frekvenser så uppstår inte fenomenet totalt sett.
Det gäller att få upp fenomenet mot högre frekvens så långt från delningsfrekvens som möjligt.
Men det finns andra faktorer som göms i en högtalares frekvensberoende spridningsegenskaper.
juanth skrev:petersteindl skrev:Rille, varför skulle du se en sådan dipp?
Det I-or beskriver är ett fenomen som uppstår vid någon frekvens hos konelement.
Är delningsfrekvensen under dessa frekvenser så uppstår inte fenomenet totalt sett.
Det gäller att få upp fenomenet mot högre frekvens så långt från delningsfrekvens som möjligt.
Men det finns andra faktorer som göms i en högtalares frekvensberoende spridningsegenskaper.
Jag tror att Rille tar i beaktande att han delar med första ordningens filter. Med elementets egen avrullning ger det ungefär 2:a ordningen i total. Då skulle det kunna påverka om där finns olinjäriteter kring drygt 3 kHz
Om man ska mäta vågfront hos ett element. Vilket minsta avstånd är att rekommendera?
Rille skrev:Det är just för spridningen som jag lägger vikt vid detta. Att inte få en svacka i sidled vid delningen utan en jämnt fallande nivå. Här är en äldre mätning på mitt projekt. Från rakt fram till 90grader i sidled. 10dB mellan strecken. Jag ser ingen fasförändring i sidled som borde ge en dipp i tonkurvan. Delning vid 2,5kHz. Ursäkta den dåliga bilden med skärmblänk, det var den jag hade i telefonen..
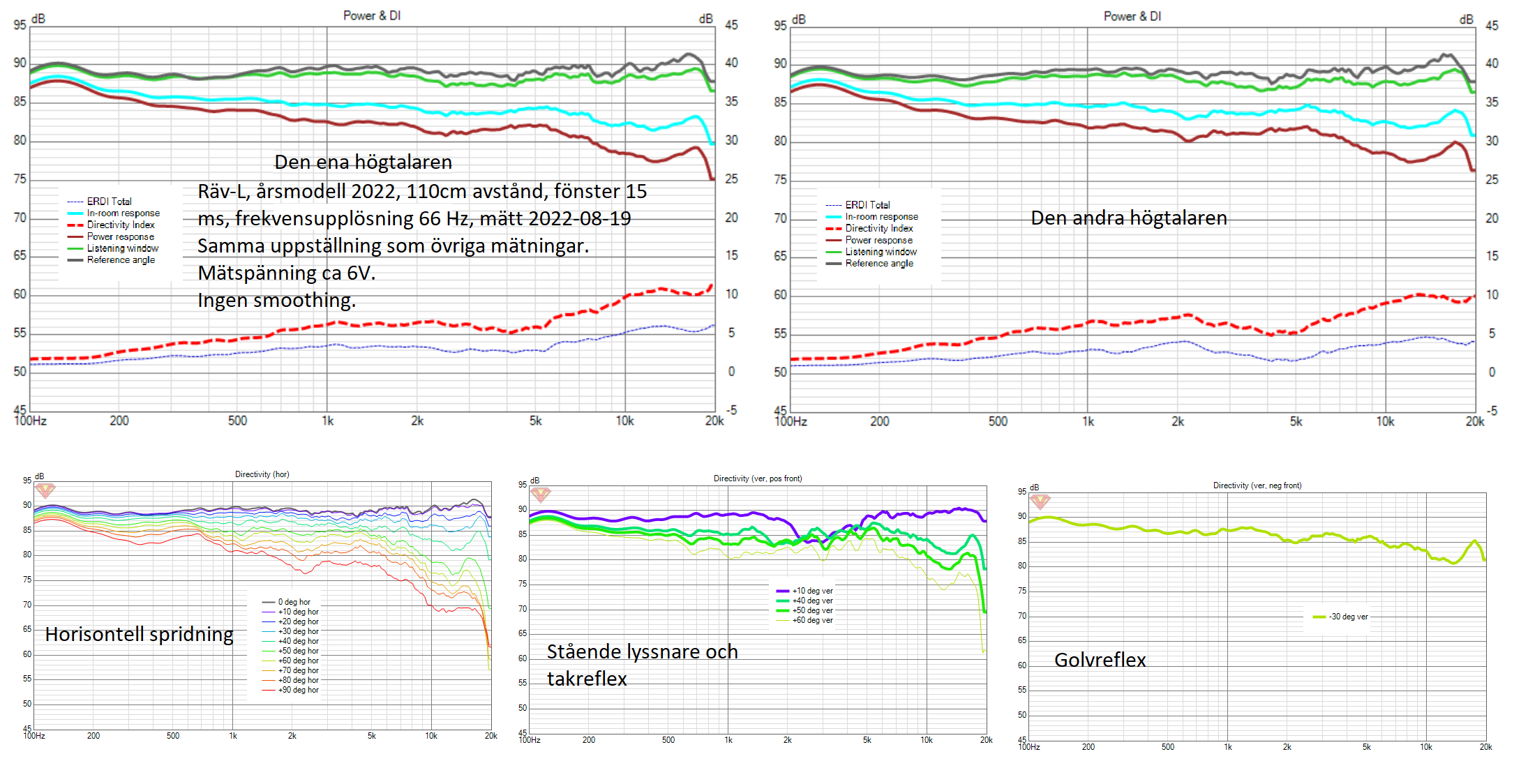
petersteindl skrev:juanth skrev:petersteindl skrev:Rille, varför skulle du se en sådan dipp?
Det I-or beskriver är ett fenomen som uppstår vid någon frekvens hos konelement.
Är delningsfrekvensen under dessa frekvenser så uppstår inte fenomenet totalt sett.
Det gäller att få upp fenomenet mot högre frekvens så långt från delningsfrekvens som möjligt.
Men det finns andra faktorer som göms i en högtalares frekvensberoende spridningsegenskaper.
Jag tror att Rille tar i beaktande att han delar med första ordningens filter. Med elementets egen avrullning ger det ungefär 2:a ordningen i total. Då skulle det kunna påverka om där finns olinjäriteter kring drygt 3 kHz
Om man ska mäta vågfront hos ett element. Vilket minsta avstånd är att rekommendera?
Mäta vågfront? Först måste man definiera vad vågfront är för något. Vad är en vågfront?
I det här fallet handlar det om ljudvågor i luften som medium.
Sedan bör man titta på egenskaper hos en ljudvågfront.
Vill man titta på ljudtryck eller ljudintensitet?
Låt säga att vi väljer ljudtryck. Ljudtryck kan mätas i form av absolut tryck i enheten Pascal Eller som en logaritmisk nivå med enheten dB. Låt säga att vi väljer det senare.
Eftersom vi diskuterar en ljudfront så måste man först titta på och begrunda en ljudfronts egenskaper innan man kan ge sig på att försöka mäta dessa egenskaper. Då man talar om en ljudfront, så kan man se fronten som en vägg. Står denna vägg still? Rör sig hela väggen i en riktning? Är väggen plan eller sfärisk eller ser den ut på något annat sätt? En vägg har en yta. En yta har enheten kvadratmeter och har 2 dimensioner. Ytan finns i en rumsdimension som har 3 dimensioner. Om ytan inte är plan utan krökt så måste ytan beskrivas i 3 dimensioner. Om ytan rör på sig, på sådant sätt att den har en hastighet, så kan man analysera ytan under förutsättning att hastigheten är konstant hos hela ytan och konstant med frekvens. Det är vågrörelse som har frekvens och våglängd som beror på hastigheten på vågfrontens förflyttning/utbredning.
Egenskaper som grupplöptid kommer in i ekvationen. Vill vi att vågfronten skall se identiskt lika ut oberoende av frekvens? Om inte, varför då? Och i så fall, hur skall önskvärd vågfront se ut?
Vad är det man vill veta och åstadkomma med en vågfront?
Om vågfronten rör sig från en plats till en annan plats, vill vi att vågfronten skall vara likadan på bägge platser? Skall den dessutom vara lika för hela tonfrekvensområdet?
Om vi börjar i någon ände och tittar på en pulserande sfär med rak frekvensgång i samtliga riktningar, så fås en sfärisk ljudfront med en konstant lika radie i samtliga riktningar där ljudvågsutbredningen konstant får ökad radie då ljudfronten utbreder sig. Ytan är alltid en sfär. Nivån på ljudtrycket minskar med större radie. Nivån minskar med 6 dB då radien fördubblas. Vågfronten är en sfär med konstant frekvensgång. Fasen ändras inte på ytan.
Frångår vi denna pulserande sfär så kommer vågfronten inte att vara sfärisk med de egenskaper som den pulserande sfären har.
Den sfäriska ytan beror på att radierna åt samtliga håll från ljudkällan kan ses som vektorer med riktning. Samtliga vektorer åt alla olika håll måste vara identiska i fas och frekvensgång. En impuls måste se likadan ut i alla riktningar.
Då bibehålls vågfronten från ljudkälla till observatör, under förutsättning att det är frifält. Detta gäller då direktljud oberoende observatörens plats i det 3-dimensionella rummet.
Vi har då åstadkommit en ytfront som utbreder sig med ljudets hastighet i ett 3-dimensionellt rum.
För att mäta detta d v s en ytutbredning, så krävs det att man mäter på tillräckligt många ställen så att man kan åskådliggöra en yta.
Om denna ytas form ser identisk ut på 2 meters avstånd som på 1 meters avstånd så har man anledning att förmoda att ytans form inte heller ändras på större avstånd än på 1 meters avstånd. Om formen är konstant men större på större avstånd så har formen ändrats linjärt. Det är egentligen enbart skalan på koordinatsystemet som behöver ändras. Det är då endast en koordinatsystemegenskap.
I allt detta så är det vektoregenskaperna som sätter resultatet. Det är då riktningsegenskaperna.
Men eftersom tryck inte har riktning och inte heller ljudtryck, så måste riktningen bestämmas på annat sätt än med ljudtryck. Det är då man måste införa ljudtrycksgradient. Det är en operator som bygger på en specifik derivata av ljudtryck på speciellt sätt. Det är skillnaden på rumskoordinater (x,y,z) då man stegar sig fram i tiden. Det är inte enkom vektorns längd som ändras som är en skalär, utan även rumskoordinaterna d v s riktning uppnås och då finns en vektor med given längd. Tryckgradienten hos ljudtryck från en punkt är den riktning som har störst ljudtrycksförändring per avstånd från punkten. Räknar man på detta så fås riktningen på tryckfronten och den är frekvensberoende hos högtalare. Finns fler ljudkällor i samma frekvensområde så summeras deras vektorer till att bli en summavektor. Summationen är enkom linjär under förutsättning att den sker i ett vektorrum, som även kallas det linjära rummet, på engelska vector space eller linear space.
Finns inte denna linjäritet så kan summavektorn bli i vilken riktning som helst.
Så, det är inte enkelt att mäta vågfront, men man måste veta vad man skall mäta för att sedan beräkna vågfronten korrekt.
Användare som besöker denna kategori: Inga registrerade användare och 7 gäster