Moderator: Redaktörer
Och läckage.Naqref™ skrev: Då har man ett Q-värde som beror (i princip) på dämpningen inne i lådan, flödesförluster i basreflexporten, flex i lådväggar, volymen samt den eqvivalenta massan i porten.
Snickers-is skrev:Q-verdien henger i høyeste grad også sammen med elementets parametre. Derfor kan man heller ikke lage en slik oversikt som du nevner.

manw skrev:Det ringde en klocka nånstans i bakhuvudet att jag i alla fall sett detta någon gång vad det gäller värdet QL. Om det nu är detta som ursprungsfrågan gäller.
Hittade det i en av mina gamla böcker "Bullok On Boxes" ISBN 0-9624191-5-X på sidan 7.
"According to Small, most systems have a QL fo between 5 and 10, with a general tendency for it to fall with increasing box volume. Thus, the asumptions of QL = 10 for small boxes, QL = 7 for moderate boxes, and QL = 5 for large boxes should be satisfactory."
Låter inte som någon exakt vetenskap direkt (eller vad liten, mittemellan och stor är), men författaren (eller Small) har kommit med ett sådant påstående i alla fall. Så står det vidare att man får mäta upp det (hur) och efterjustera "alignment" efter detta.
IngOehman skrev:Kan även tillägga att man nog bör räkna ursprunget till de tvenne resonansvilligheterna lite annorlunda än vad som antytts...
Jag menar att portens Q (kallades nyss Qp, men kallas ofta Qh) beror inte bara av resonansfaktorernas produkt delat med portens egna förluster, utan hit hör även en del av förlusterna i lådans inre, såsom varandes signifikant bidragande.
Svante skrev:Mja, så kan man ju göra och då har man en resultatinriktat synsätt. Om jag förstår dig rätt. Du vill veta Q-värdet som helmholtzresonatorn skulle ha om man täppte igen elementöppningen? Jo, så kan man förstås göra, men då blandar man ju ihop de två orsakerna, nämligen dämpning i låda och dämpning i port.
manw skrev:Svante skrev:Mja, så kan man ju göra och då har man en resultatinriktat synsätt. Om jag förstår dig rätt. Du vill veta Q-värdet som helmholtzresonatorn skulle ha om man täppte igen elementöppningen? Jo, så kan man förstås göra, men då blandar man ju ihop de två orsakerna, nämligen dämpning i låda och dämpning i port.
Jo, det var väl så jag tolkade grundfrågan, och som man i boken behandlade det, att man diskuterade den (empiriskt funna) Helmholzresonatorns Q-värde.
Att försöka bestämma Q-värdet hos porten respektive lådan separat ligger nog över min nivå i alla fall
manw skrev:förstår inte din beskrivning i ekvivalentschemat av "Vent" i Basta-hjälpen, men det kanske finns beskrivet någon annanstans.
PeterAkemark skrev: Tätheten lådorna var mätt med porten tillsluten och en voltmeter ansluten över baselementet. Baselementets membran pressades in 1-2 mm före förslutningen av porten och den uppstående emk´n över talspolen mättes när membranet släppdes. Tiden tills emk'n var 0 mättes och var omkring 3-4 sekunder eller längre.
Svante skrev:IngOehman skrev:Kan även tillägga att man nog bör räkna ursprunget till de tvenne resonansvilligheterna lite annorlunda än vad som antytts...
Jag menar att portens Q (kallades nyss Qp, men kallas ofta Qh) beror inte bara av resonansfaktorernas produkt delat med portens egna förluster, utan hit hör även en del av förlusterna i lådans inre, såsom varandes signifikant bidragande.
Mja, så kan man ju göra och då har man en resultatinriktat synsätt. Om jag förstår dig rätt. Du vill veta Q-värdet som helmholtzresonatorn skulle ha om man täppte igen elementöppningen? Jo, så kan man förstås göra, men då blandar man ju ihop de två orsakerna, nämligen dämpning i låda och dämpning i port. Det blir lite som om du vill ha ett Qts-värde för lådan (som ju beror av Qms och Qes i elementfallet).
Svante skrev:Jag separerar dem faktiskt hellre eftersom jag hellre ser det som en förklaringsmodell, ett sätt att beskriva de två förlustresistanserna.
IngOehman skrev:Håll med mig!
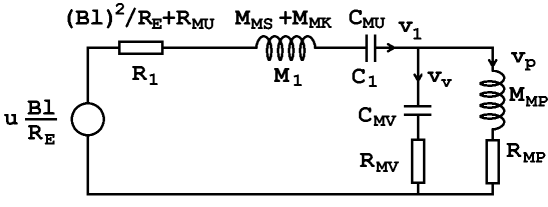
IngOehman skrev:Gillar inte dina analogischemor.
IngOehman skrev:(De är bättre, för man kan så mycket snyggare följa energins väg genom högtalarelement och låda. Tycker även fördelen att insignalen (elektrisk) får vara insignal i modellen, är ett givet plus!)

Svante skrev:PeterAkemark skrev: Tätheten lådorna var mätt med porten tillsluten och en voltmeter ansluten över baselementet. Baselementets membran pressades in 1-2 mm före förslutningen av porten och den uppstående emk´n över talspolen mättes när membranet släppdes. Tiden tills emk'n var 0 mättes och var omkring 3-4 sekunder eller längre.
Hmm, det var ingen bra metod. 0,0 volt eller 0,0000 volt? Hur liten måste spänningen vara för att vara noll? Det vore bättre att registrera tidskonstanten, dvs den tid det tar för spänningen att sjunka till 1/e gånger släppspänningen.
PeterAkemark skrev:Svante skrev:PeterAkemark skrev: Tätheten lådorna var mätt med porten tillsluten och en voltmeter ansluten över baselementet. Baselementets membran pressades in 1-2 mm före förslutningen av porten och den uppstående emk´n över talspolen mättes när membranet släppdes. Tiden tills emk'n var 0 mättes och var omkring 3-4 sekunder eller längre.
Hmm, det var ingen bra metod. 0,0 volt eller 0,0000 volt? Hur liten måste spänningen vara för att vara noll? Det vore bättre att registrera tidskonstanten, dvs den tid det tar för spänningen att sjunka till 1/e gånger släppspänningen.
Nä, det var aldrig ett problem. Det var mer en fråga om att se förhållandet mellan helt öppen port och försluten port. Jag minns att jag använde en deriveringskrets för att tydligare se konrörelsen. Tiden var ofta väsentligt längre än 4 sekunder, mera åt 30-40 sekunder. Mycket beroende på det använda elementet. Det var det som läckte i huvudsak
PeterAkemark skrev:Svante:
Visst är det logiskt att göra som du föreslår, det vara bara det att jag inte gjorde det, då. Det var ett sätt att kvantifiera läckaget på den tiden - omkring 1975. När allt gjordes med räknesticka och en TI-59 (programmerbar kalkylator, magnetremsor)
PeterAkemark skrev:Svante skrev:PeterAkemark skrev: Tätheten lådorna var mätt med porten tillsluten och en voltmeter ansluten över baselementet. Baselementets membran pressades in 1-2 mm före förslutningen av porten och den uppstående emk´n över talspolen mättes när membranet släppdes. Tiden tills emk'n var 0 mättes och var omkring 3-4 sekunder eller längre.
Hmm, det var ingen bra metod. 0,0 volt eller 0,0000 volt? Hur liten måste spänningen vara för att vara noll? Det vore bättre att registrera tidskonstanten, dvs den tid det tar för spänningen att sjunka till 1/e gånger släppspänningen.
Nä, det var aldrig ett problem. Det var mer en fråga om att se förhållandet mellan helt öppen port och försluten port. Jag minns att jag använde en deriveringskrets för att tydligare se konrörelsen. Tiden var ofta väsentligt längre än 4 sekunder, mera åt 30-40 sekunder. Mycket beroende på det använda elementet. Det var det som läckte i huvudsak
Användare som besöker denna kategori: Inga registrerade användare och 25 gäster