Moderator: Redaktörer
silverminken skrev:Hej!
Hur beräknar man avstämningsfrekvens för en rektangulär port med en icke konstant tvärsnittsarea à la Paa?
Och hur ska man tänka med minsta tvärsnittsarean på porten i förhållande till elementens luftflyttningsförmåga?
Jag tror inte att jag har någon programvara som kan räkna på detta, kanske någon som har något tips, länk eller trevliga formler?
LypsylateX skrev:Ges inte avstämningsfrekvensen bara av portens volym? Så om din rektangulära port har samma volym som en rund som ger en viss avstämningsfrekvens så blir det samma... då är det inte så svårräknat.
Ps. Jag kan ha skitfel. ;D
Naqref™ skrev:LypsylateX skrev:Ges inte avstämningsfrekvensen bara av portens volym? Så om din rektangulära port har samma volym som en rund som ger en viss avstämningsfrekvens så blir det samma... då är det inte så svårräknat.
Ps. Jag kan ha skitfel. ;D
Det räcker att säga att du har skitfel. Vi behöver inte gnida in det mer än så.
perstromgren skrev:Hur skitfel då? Jag trodde nämligen samma sak, att det är luftens massa i porten (och indirekt alltså dess volym) som tillsammans med andra komponenter i systemet utgör resonanskrets.
perstromgren skrev:
Hur skitfel då? Jag trodde nämligen samma sak, att det är luftens massa i porten (och indirekt alltså dess volym) som tillsammans med andra komponenter i systemet utgör resonanskrets.
silverminken skrev:Aj då är det så illa...
Ok har ni något tips på hur man ska höfta då?
Kan man tänka sig så här kanske? Räkna fram ett lämpligt rör som skulle göra jobbet. Tänk dig en rektangulär port med samma tvärsnittsarea och längd. Vinklar man sedan upp ändarna så att de får lite större area så borde väl resonansfrekvensen öka eller tänker jag fel? Kanske sisådär 20% med en lämplig uppvinkling?
Låter det totalfel?
Naqref™ skrev:Det räcker att säga att du har skitfel. Vi behöver inte gnida in det mer än så.
Svante skrev:Jo, om man tänker sig röret som två stumpar efter varandra, med olika diameter, så blir det mycket enklare att räkna på de akustiska storheterna.
silverminken skrev:Aj då är det så illa...
Ok har ni något tips på hur man ska höfta då?
Kan man tänka sig så här kanske? Räkna fram ett lämpligt rör som skulle göra jobbet. Tänk dig en rektangulär port med samma tvärsnittsarea och längd. Vinklar man sedan upp ändarna så att de får lite större area så borde väl resonansfrekvensen öka eller tänker jag fel? Kanske sisådär 20% med en lämplig uppvinkling?
Låter det totalfel?
paa skrev:Svante skrev:Jo, om man tänker sig röret som två stumpar efter varandra, med olika diameter, så blir det mycket enklare att räkna på de akustiska storheterna.
Ok, Svante, du som gillar att räkna;
Antag att man har en låda på säg 10 liter och ett säg 20 cm långt basreflexrör som ger en avstämning på säg 30 Hz. Om man då sågar av det röret efter 10 cm (vid mitten) och i stället kopplar ihop det med ett 10 cm långt rör med dubbla arean, vilken avstämningsfrekvens skulle du säga vi har fått då? Det borde ge en uppfattning om storleksordningen av det vi diskuterar.
Challe skrev:En fråga jag ställde i en anna tråd är hur portresonanserna påverkas.
Bestäms de av den luftmassa som fjädrar eller spelar portens utformning någon avgörande roll?
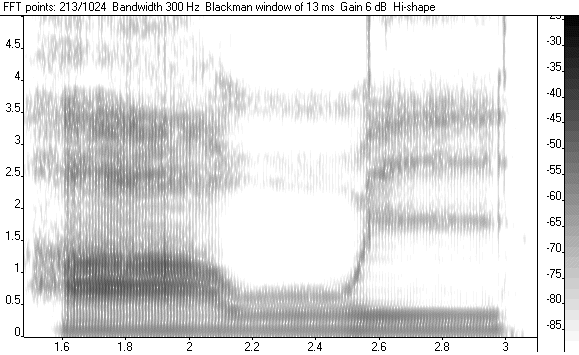
Svante skrev:
Så här flytter sig formanterna (=resonanserna) när jag säger A-O-I:
perstromgren skrev:
Å, jösses! Den där utskriften ser ju som det kommer direkt från den gamla trumskrivaren vi använde för 30 år sedan, men det gör det väl inte, säg?
Naqref™ skrev:perstromgren skrev:
Å, jösses! Den där utskriften ser ju som det kommer direkt från den gamla trumskrivaren vi använde för 30 år sedan, men det gör det väl inte, säg?
Gissningsvis är det en skärmdump av en datorgenererad bild som baserar sig på fysiska data.
Svante skrev:paa skrev:Svante skrev:Jo, om man tänker sig röret som två stumpar efter varandra, med olika diameter, så blir det mycket enklare att räkna på de akustiska storheterna.
Ok, Svante, du som gillar att räkna;
Antag att man har en låda på säg 10 liter och ett säg 20 cm långt basreflexrör som ger en avstämning på säg 30 Hz. Om man då sågar av det röret efter 10 cm (vid mitten) och i stället kopplar ihop det med ett 10 cm långt rör med dubbla arean, vilken avstämningsfrekvens skulle du säga vi har fått då? Det borde ge en uppfattning om storleksordningen av det vi diskuterar.
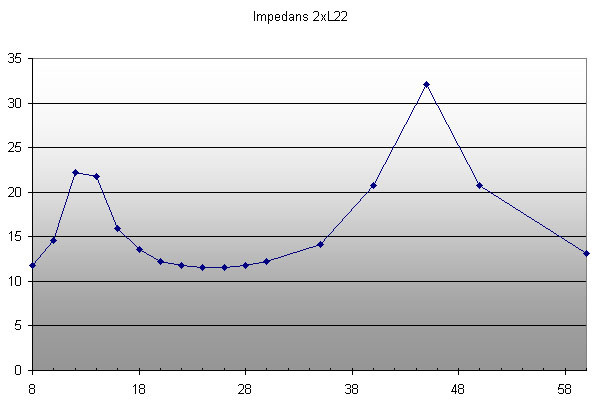
Ok, den akustiska massan är ju
Ma=rho0*L/S
I första fallet består den av två lika delar, om vi tänker oss att vi delar (mentalt) även det röret på mitten. I andra fallet så får ena halvan dubbla arean, dvs halva akustiska massan (när S blir dubbelt så stor). Det som förut var 2 massenheter blir nu bara 1,5. Ändringen i akustisk massa blir en faktor 1,5/2=3/4=0,75. Eftersom resonansfrekvensen är proportionell mot 1/√Ma så blir resonansfrekvensen 1,15 ggr högre, eller 34,6 Hz. Lådvolymen och absoluta rörlängden var redundant information.
I verkligheten blir det lite annorlunda eftersom ändkorrektionen ändras när rördiametern ändras. Men det är en annan femma.
Användare som besöker denna kategori: Inga registrerade användare och 16 gäster