Behringer vs Earthworks, mikrofonmätning.

[celef]

Ok, om jag tar ett tidsfönster på 1 ms och nollpaddar, dvs lägger till 3 ms med nollor. Så gör jag en FFT på 4 ms. Är alla punkterna som kommer ur FFTn mätpunkter då?

inte vet jag men du vet, saken jag vill ha fram är sann upplösning

vad jag heller inte förstår är smooth-funktionen, om jag kör gejtat 4ms (250-500-750-1000-1250-1500-1750-2000-2250-2500-2750-3000... upplösning) plus smoothing 1/3 okt; är då nåt av det jag ser på skärmen sant?

[Svante]

Alltså, så här är det.

En FFT lämnar data på linjär skala, dvs frekvensena för datapunkterna ligger tex på (0), 10, 20, 30, 40, 50 ... 22020, 22030, 22040, (22050).

Visar man det här på logskala så blir det väldigt mycket tätare mellan punkterna till höger. Bandbredden i det här exemplet är ett konstant antal Hz, någonstans i trakterna av 10 Hz.

På den gamla goda tiden när man hade en kurvskrivare som hade en begränsad skrivhastighet och man körde med logsvep, så fick man en filterverkan som fick en bandbredd som blev proportionell mot frekvensen. Bandbredden var kanske 10 Hz vid 20 Hz, men 100 Hz vid 200 Hz och 1000 Hz vid 2000 Hz. Bandbredden var ett visst antal delar av en oktav, tex 1/3.

Det där gamla sättet att visa en kurva är rätt trevligt, men passar illa med en FFT, och därför har man med viss rätt implementerat den filtrering som fanns i de gamla kurvskrivarna.

Så till mitt exempel med nollpaddningen då. Om man lägger till nollor som jag beskrev det så kommer var fjärde punkt att bli som i den korta FFTn och punkterna däremellan blir runt och mjukt interpolerade (med sincar faktiskt). Förmodligen är den interpolationen bättre än bara räta linjer mellan datapunkterna i den meningen att de förmodligen ligger närmare det verkliga värdena mellan punkterna. Nackdelen är att man inte ser datapunkterna lika tydligt.

Så här:




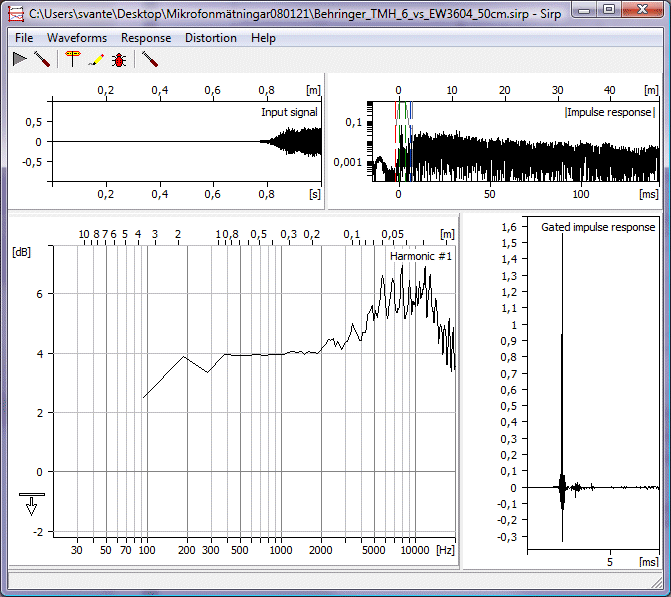
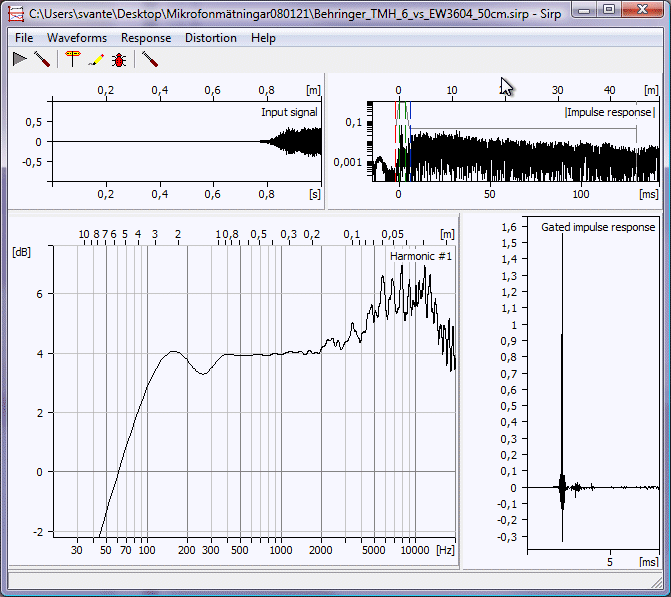
I den andra bilden är det ju mycket snyggare och förmodligen riktigare runt 200 Hz, men förädiskt lätt att tolka som att mikrofonen i fråga har ett kraftigt basfall. Det har den inte, fönstret är för kort bara.

[celef]

dottar skulle funka, ser riktigt informativt ut tycker jag själv

antingen hardcore-varianten till vänster för dom tuffa och för dom löskokta mellantinget till höger

[Jocke]

Hmmm...

Brukar man inte säga att den ideala högtalaren är en punktformig ljudkälla?

/Jocke

[Svante]

Hmmm...

Brukar man inte säga att den ideala högtalaren är en punktformig ljudkälla?

/Jocke

Det beror nog på vem "man" är och vad mannen ifråga anser vara idealt.

Alltså, ordet "idealt" låter ju väldigt fint, men det brukar bara stå för en modell av något som är förenklad. Den kan vara ideal även om den är dålig.

[rikkitikkitavi]

dottar skulle funka, ser riktigt informativt ut tycker jag själv

antingen hardcore-varianten till vänster för dom tuffa och för dom löskokta mellantinget till höger

nja, du får nog öka frekvensupplösningen lite? vad, har inte datorn tillräckligt med MHz o MB ? klenis

kan vara lite svårt att se hur kurvan går i de lägre frekvenserna. Men vad är det du mäter under 300 Hz ändå med gatade mätningar?

[Svante]

nja, du får nog öka frekvensupplösningen lite? vad, har inte datorn tillräckligt med MHz o MB ? klenis

Alltså, det där hänger ju inte på datorkraft utan på det faktum att tidsfönstret måste vara kort för att bli av med rumsreflexerna.

[celef]

kan vara lite svårt att se hur kurvan går i de lägre frekvenserna. Men vad är det du mäter under 300 Hz ändå med gatade mätningar?

nja, jag vill ju bara belysa den sanna mätupplösningen, jag vill bli påmind om detta och det bästa vore om det syntes på mätningen direkt. och att bli påmind att byta samplingsfrekvens för lågbasmäting som exempel, och mls och fft storlekar

[Svante]

kan vara lite svårt att se hur kurvan går i de lägre frekvenserna. Men vad är det du mäter under 300 Hz ändå med gatade mätningar?

nja, jag vill ju bara belysa den sanna mätupplösningen, jag vill bli påmind om detta och det bästa vore om det syntes på mätningen direkt. och att bli påmind att byta samplingsfrekvens för lågbasmäting som exempel, och mls och fft storlekar

Mm, det där är en av de svåraste problemen när man skriver program; hur styr man användaren att göra "rätt" av sig själv? Det är två helt olika saker att skriva ett program som kan göra många saker och ett som får användaren att göra rätt saker. Det är nästan ett motsatsförhållande mellan dem.

[IngOehman]

Min uppfattning är att det bästa vore att aldrig tillåta redovisning av kurvor i frekvensområden där mätproceduren som sådan ger falska och/eller opålitliga data. Det är lika fel att sätta falska dottar, som att interpolera/extrapolera fram en kurva som passerar dottarna.

Det minst vidriga vore kanske att helt frankt ta bort den del av kurvan som är helt opålitlig (man får först välja en opålitlighetstolerans). Eller möjligen att redovisa den med toleranserna (som en mot låga frekvenser växande tratt).

Hmmm...

Brukar man inte säga att den ideala högtalaren är en punktformig ljudkälla?

/Jocke

Folk påstår mycket som är ogenomtänkt.


Vh, iö

[Jocke]

Appropå:

dottar skulle funka

/J

[rikkitikkitavi]

nja, du får nog öka frekvensupplösningen lite? vad, har inte datorn tillräckligt med MHz o MB ? klenis

Alltså, det där hänger ju inte på datorkraft utan på det faktum att tidsfönstret måste vara kort för att bli av med rumsreflexerna.

jo, jag vet . du förklarade det lite längre upp i tråden. Ironin gick inte riktigt hem. Att det bara hänger på datorkraft o inte mätuppställningen, lätt att gå förlorat när man blir lite "isolerad" mha ett program som gör en massa man inte riktigt förstår.

Det är knepigt att mäta. (nu talar jag allmännt, inte bara akustik)

Om man aldrig interpolerade skulle vi inte ha data , ialla fall inte med mätsystem där man samplar signalen. En rimlig frekvensupplösning dikteras ju av huruvida den är tillräcklig för att man skall kunna göra sitt arbete med mätobjektet.

[IngOehman]

Ekofia rum underlättar sådana här mätningar, och det behöver faktiskt inte vara ekofritt så speciellt långt ned i frekvens (så länge man inte blandar kulor och njurar), när man mäter mot referens.

Det är väldigt lätt att snabbbygga ett litet halvgenomsläppligt "mätbås" som gör susen prima väl. (Undvik att de inre absorptionsytorna får konkav form.)


Vh, iö

- - - - -

PS. Bra ljudkälla för sådana här referensade mätningar är en 2" mellanregisterdome av god kvalitet, helst nedsänkt i golvet. Möjligen kan man dela den lågt till ett baselement också, för lägre ljudgeneratordist och bättre S/N vid låga frekvenser.

[Jocke]

Det är knepigt att mäta.

Mm, det där är en av de svåraste problemen när man skriver program; hur styr man användaren att göra "rätt" av sig själv? Det är två helt olika saker att skriva ett program som kan göra många saker och ett som får användaren att göra rätt saker. Det är nästan ett motsatsförhållande mellan dem.

Eftersom det nu är en allmän ståndpunkt här att mätning är nödvändig för att förklara och bekräfta det vi upplever. Visst är det viktigt att det blir rätt för att vi ska kunna utläsa något ur resultatet men framför allt tror jag att vad de flesta av oss behöver är ett hyggligt verktyg (tex Tombstone och ECM8000) som inte ruinerar oss.

Sedan är det naturligtvis bra om vi kan resonera kring vilka rutiner för mätningar som ger korrekta och jämförbara resultat. Sedan är det en viktig sak: Tillgången till kamraterna på faktiskt.se

Om man sätter ambitionerna för högt och börjar på toppen finns det bara en väg därifrån - nedåt!

Jag tycker att Svante bör ha rejält med "cred" för sitt engagemang!

/Jocke

[Svante]

Min uppfattning är att det bästa vore att aldrig tillåta redovisning av kurvor i frekvensområden där mätproceduren som sådan ger falska och/eller opålitliga data. Det är lika fel att sätta falska dottar, som att interpolera/extrapolera fram en kurva som passerar dottarna.

Instämmer. Det kan dock vara ett närapå lika stort arbete att räkna ut felet som att räkna ut kurvan, så det där önskvärda är inte alltid så lätt att få till. Man vill ju inte stänga av funktionalitet som kan tänkas vara användbar, men man vill heller inte presentera data som kan vara felaktiga. Och en mätning som är felaktig i ett sammanhang kan vara riktig i ett annat.

Även om man kan hjälpa användaren så går det nog inte att komma ifrån att man faktiskt måste förstå mätmetoderna ibland. Det kan vara lite svårt att få in i dagens trycka-på-knappen-datorn-fixar-nog-det-där-samhälle.

[RogerGustavsson]

Som alternativ till en okalibrerad ECM8000 är väl Ibf Akustiks EMM-8 ett bra val?

[Svante]

Ekofia rum underlättar sådana här mätningar, och det behöver faktiskt inte vara ekofritt så speciellt långt ned i frekvens (så länge man inte blandar kulor och njurar), när man mäter mot referens.

Det är väldigt lätt att snabbbygga ett litet halvgenomsläppligt "mätbås" som gör susen prima väl. (Undvik att de inre absorptionsytorna får konkav form.)


Vh, iö

- - - - -

PS. Bra ljudkälla för sådana här referensade mätningar är en 2" mellanregisterdome av god kvalitet, helst nedsänkt i golvet. Möjligen kan man dela den lågt till ett baselement också, för lägre ljudgeneratordist och bättre S/N vid låga frekvenser.

Mm, jag har ju använt ett 1" diskantelement i en vanlig högtalarlåda som källa och det tror jag är det största problemet. Jag gejtar ju impulssvaret, så mätbåset blir onödigt, i varje fall vid det här frekvenserna. Jag leker just nu med tanken att bygga en "bula" med en tunn 1" diskant att lägga på golvet. Även om det är frestande att ta fram sticksågen och såga ett hål i sovrumsgolvet, mitt i rummet, så tror jag att det skulle stöta på patrull.

[Svante]

Sedan är det naturligtvis bra om vi kan resonera kring vilka rutiner för mätningar som ger korrekta och jämförbara resultat. Sedan är det en viktig sak: Tillgången till kamraterna på faktiskt.se

Javisst. En viktig del i det där är också att man faktiskt vågar visa hemska kurvor som man har mätt upp. Kurvorna som jag har visat i den här tråden är just såna som man får när inte allt ännu är optimalt. Får man bara se kurvor som de i mikrofondatabladen så är det lätt att bli avskräckt när man gör sin första mätning och ingenting ser ut som när proffsen gör mäter.

Fina kurvor imponerar. Fula kurvor inspirerar.

[Svante]

nja, du får nog öka frekvensupplösningen lite? vad, har inte datorn tillräckligt med MHz o MB ? klenis

Alltså, det där hänger ju inte på datorkraft utan på det faktum att tidsfönstret måste vara kort för att bli av med rumsreflexerna.

jo, jag vet . du förklarade det lite längre upp i tråden. Ironin gick inte riktigt hem.

[phon]

Jag leker just nu med tanken att bygga en "bula" med en tunn 1" diskant att lägga på golvet. Även om det är frestande att ta fram sticksågen och såga ett hål i sovrumsgolvet, mitt i rummet, så tror jag att det skulle stöta på patrull.

Nämen alltså, bara för att gravitationen finns så behöver man inte använda golvet.

Vad är det för fel på en vanlig fyrfot åtta spånskiva? Om miken ändå stämmer hyfsat under några kHz så behövs ju inte ett helt golv, det räcker med en skiva som är tillräckligt stor för att baffelsteget skall ligga under de frekvenser man mäter.

Om du ändå absolut vill stråla uppåt så går det ju bra att lägga skivan på golvet. Annars är den mer ur vägen om den hänger i taket och strålar nedåt, där dämpar dessutom mattan en del reflexer.

[rikkitikkitavi]

jo, jag vet . du förklarade det lite längre upp i tråden. Ironin gick inte riktigt hem.

Äh, det var nog jag som var lite för "o-ironisk" för att det skulle gå hem. Du kunde ju inte veta att jag visste, så att säga. ´

Fortsätt skriva i tråden, alla. Sådana här trådar är oehört pedagogiska.


Går det inte lika bra med kartongbitar? Förutsättningen är ju att eventuella skarvar är små.
Men phons ide med spånskivor, kombinerat med en "ljudhuv" kan ju vara något?

[RogerJoensson]

Ekofia rum underlättar sådana här mätningar, och det behöver faktiskt inte vara ekofritt så speciellt långt ned i frekvens (så länge man inte blandar kulor och njurar), när man mäter mot referens.

Det är väldigt lätt att snabbbygga ett litet halvgenomsläppligt "mätbås" som gör susen prima väl. (Undvik att de inre absorptionsytorna får konkav form.)

Frågan i det här fallet är om det inte ändå blir renare mätning av diskanten med kort eller variabelt tidsfönster. De båda mikarna har ju faktiskt olika riktverkan i översta oktaven och ev. små reflexer kommer att ge stora utslag. Det är klart har man en väldigt bra absorbent så kanske...

Jag lägger en slant på kort eller variabelt tidsfönster och medelvärdesutjämning (tex med bredden 1/12 oktav) före referenskompensation (för mätning av diskantregistret). Då slipper man krångla med ett bås och får stabila mätningar på ett enkelt sätt:


Panasonic 6mm kapsel (Ref.mik Earthworks M30), 5ms fyrkantigt tidsfönster, 0.7m avstånd, MLS, medelvärdesutjämnad före referenskompensation med bandbredd 1/12 oktav.

Det mesta av oroligheterna (+-0,2dB) är rester från högtalarens små oroligheter. Om man går ner till 1/6 oktavs bandbredd försvinner dessa nästan helt.

Om man kompenserar för kapselns frekvensgång (går även att göra med exemplaranpassad Eq i mikrofonen), så är den definitivt tjänlig för kvalitativa högtalarmätningar!

[Svante]

Ja, då har jag mätt dist på mik nummer 6 också.

[rikkitikkitavi]

varför ökar 3e disten när SPL sjunker? Men inte 2d?

Är det bruset som dyker upp som 3e tons dist?

vad har du för mikförstärkare?

Du måste ha mätt inne i lådan , med tanke på att mätningen går upp en bit ljudtrycksnivå ? eller så har du ett väldigt potent system , och en tolerant familj (och grannar i de högsta dB talen

intressant, mycket intressant.

[Svante]

varför ökar 3e disten när SPL sjunker? Men inte 2d?

Är det bruset som dyker upp som 3e tons dist?

vad har du för mikförstärkare?

Du måste ha mätt inne i lådan , med tanke på att mätningen går upp en bit ljudtrycksnivå ? eller så har du ett väldigt potent system , och en tolerant familj (och grannar i de högsta dB talen

intressant, mycket intressant.

Nja, tredje delton under 110 dB är nog inte så tillförlitlig. Jag driver högtalaren med ett ganska billigt PA-slutsteg som brummar en del, så det finns deltoner vid 150 och 250 Hz, ganska nära andra och tredje deltonen för 80 Hz.När disten blir svag flyter det ihop en del.

Mikrofonförstärkaren är en Symetrix nånting, det dög inte med USB-ljudkortet, det kunde inte dämpa signalen tillräckligt mycket. Det är ju ganska starkt. Symetrix-burken har en knapp som heter 15 dB pad, den var bra .

Och ja, det var inuti lådan så nivån ute i rummet var inte i närheten av 130 dB. Det var på jobbet, så det var bara rumskompisen som drabbades. Han är van.

[Svante]

Jag passade på att mäta med Earthworksmiken samtidigt. Här är jag dock inte säker på om det är högtalaren eller mikrofonen som distar. Jag mätte med en annan finare mikrofon också (DPA4066) och den gav ett snarlikt resultat, så kanske är det här högtalardist.

[Svante]

Jag leker just nu med tanken att bygga en "bula" med en tunn 1" diskant att lägga på golvet. Även om det är frestande att ta fram sticksågen och såga ett hål i sovrumsgolvet, mitt i rummet, så tror jag att det skulle stöta på patrull.

Vad är det för fel på en vanlig fyrfot åtta spånskiva? Om miken ändå stämmer hyfsat under några kHz så behövs ju inte ett helt golv, det räcker med en skiva som är tillräckligt stor för att baffelsteget skall ligga under de frekvenser man mäter.

Mja... Nuskavise. Det är alltså avståndet till första reflexen som bestämmer hur långt ner i frekvens man kan mäta. Att fälla in källan i golvet är ju ett sätt att maximera avståndet till den i ett vanligt rum. Oftast blir det takreflexen som blir första reflexen och den anländer vid en tidpunkt som motsvarar 2x avståndet mellan mik och tak efter direktljudet, typiskt kanske 2x1,5=3 meter. Detta är vad baffeln har att konkurrera med, man måste få 3 meters längre löpväg för kantreflexen. Det blir en ganska stor spånskiva det.

...fast å andra sidan är det ju bara om man ska ner så långt som möjligt i frekvens, det är ju inte säkert att man vill det.

[lilltroll]

Jag passade på att mäta med Earthworksmiken samtidigt. Här är jag dock inte säker på om det är högtalaren eller mikrofonen som distar. Jag mätte med en annan finare mikrofon också (DPA4066) och den gav ett snarlikt resultat, så kanske är det här högtalardist.

Kan du inte porta lådan och mäta vid fp, med ordentlig portdiameter. Borde minska både 2:a och 3:e genererat från elemenetet. Det är väl ELAK lådan ?

[IngOehman]

Min uppfattning är att det bästa vore att aldrig tillåta redovisning av kurvor i frekvensområden där mätproceduren som sådan ger falska och/eller opålitliga data. Det är lika fel att sätta falska dottar, som att interpolera/extrapolera fram en kurva som passerar dottarna.

Instämmer. Det kan dock vara ett närapå lika stort arbete att räkna ut felet som att räkna ut kurvan, så det där önskvärda är inte alltid så lätt att få till. Man vill ju inte stänga av funktionalitet som kan tänkas vara användbar, men man vill heller inte presentera data som kan vara felaktiga. Och en mätning som är felaktig i ett sammanhang kan vara riktig i ett annat.

Även om man kan hjälpa användaren så går det nog inte att komma ifrån att man faktiskt måste förstå mätmetoderna ibland. Det kan vara lite svårt att få in i dagens trycka-på-knappen-datorn-fixar-nog-det-där-samhälle.

Instämmer. I allt.

Men den praktiska verkligheten är ändå den, att "alla användares insikt i mätmetodens/presentationens brister", är en utopisk dröm.

Därför menar jag att den som skapar mätprogrammet trots allt får förmodas ha ett kunskapsövertag över rätt många av programmets
användare - och har därför ett ansvar (möjlighet att ta ett i varje fall) att hjälpa användaren att inte dra några felaktiga slutsatser,
genom att utforma presentationen således att den inte framställer gissningar som sanningar.

(Det gäller för maskiner - och för människor. )


Vh, iö

[lilltroll]

Oehman: En 2" fullrange-konhögtalare som är tämligen fri från (stygga) uppbrytningar, skulle det kunna fungera? Fördelen är att fs = 150 Hz.

Jag har själv provat i en 2*2 meters baffel med trunkering alá log-chirp. Referensmikrofonen fick vara ensam mikrofon under mätningen, därefter mättes objektet ensamt. Fick jättefina kurvor utan smoothing.
Diskanten var en Scanspeak 9300.

En sytråd med en vikt i som lod från taket eller stativ är praktiskt för att hamna på samma ställe varje gång i rummet.