Zaph omvärderar höga Q.

[Jocke]

På sin blog http://www.zaphaudio.com/blog.html skriver Zaph bla:

So, in the case of the RS100 8ohm with a .8 Qts for example, most brainless box response programs will recommend a too-large box with no consideration of what baffle step does to the response. Using a "normal" enclosure size with a high Qtc, after factoring in baffle step you'll see that the high Qts bass peaking doesn't look so bad - in fact it's nearly not there.

/J

[paa]

Slutsatsen han drar är inte fel heller:

People need to realize that smart, real world enclosure design requires more than what most of these box response programs provide.

[skrutten]

Måste zaph stämma om alla sina högtalare nu då??

VVVVVVVVVVV

[Kaffekoppen]

Nä, han är mest sur för att han lagt stora pengar på spolar förut

...oavsett så brukar höga q-värden resultera i allt annat än djupgående system?

[rikkitikkitavi]

Nä, han är mest sur för att han lagt stora pengar på spolar förut

...oavsett så brukar höga q-värden resultera i allt annat än djupgående system?

inte om man ringer Mr. Linkwitz...

Men då måste man ju bygga elektronik (eller så har man en parametrisk EQ av förträffligt slag)

[Naqref]

...oavsett så brukar höga q-värden resultera i allt annat än djupgående system?

Beror ju på vad man menar med höga Q men om man håller sig i normalintervallet så är det omvända snarare mer relevant. Låga Q omöjliggör djupbas.

[Jocke]

...oavsett så brukar höga q-värden resultera i allt annat än djupgående system?

Beror ju på vad man menar med höga Q men om man håller sig i normalintervallet så är det omvända snarare mer relevant. Låga Q omöjliggör djupbas.

Relaterat till resonansfrekvensen!

/J

[Naqref]

Nu avsåg jag det som en fri parameter där alla andra hålls konstanta. Då får man svagare djupbas med lägre Q hos elementet än om man har något högre Q.

[Kraniet]

ett qts på 0.8 tycker jag nog är lite väl högt. iaf vad gäller de högtalare jag vill bygga.

men många kommersiella högtalare har ju ofta högt q i basen. många personer föredrar q uppåt 1.0 då basen upplevs "bättre". Små högtalare har ju ofta det tricket med en puckel i 70hz området så man ska bli lurad att dom går djupt.

men personligen upplever jag lågt Q som bättre.

[Jocke]

Nu avsåg jag det som en fri parameter där alla andra hålls konstanta. Då får man svagare djupbas med lägre Q hos elementet än om man har något högre Q.

Det är det jag menar! Tänkte mer på att slippa en diskussion om definitioner genom att relatera Q till Fs.

/Jocke

[Jocke]

ett qts på 0.8 tycker jag nog är lite väl högt. iaf vad gäller de högtalare jag vill bygga.

men många kommersiella högtalare har ju ofta högt q i basen. många personer föredrar q uppåt 1.0 då basen upplevs "bättre". Små högtalare har ju ofta det tricket med en puckel i 70hz området så man ska bli lurad att dom går djupt.

men personligen upplever jag lågt Q som bättre.

...eller om man ska se det som ett sätt att få små högtalare "användbara"? Att tvinga ut riktigt låg bas ut ett litet element upplever jag som en bortkastad ambition då andra faktorer ändå kommer att begränsa återgivningen!

/Jocke

[Svante]

Bara så vi vet vad vi pratar om. Här är några olika system med olika Qts i olika lådor:



...och samma system när man har räknat med baffelsteget.



Det är inte helt enkelt att jämföra olika Qts, eftersom man lämpligen ändrar lådvolym och avstämning också. Rör och blå kurva är exempel på att man bara har ändrat Qts (svarta kurvan är utgångspunkten), ljusblå och ljusröd har man i stället använt Ingvars "leksaksformler" för att bestämma lämplig lådvolym och avstämning.

[Jocke]

En gång i tiden lyckades jag lära mig lite av de här sambanden genom ett kompendium som "McBruce" (nick) var inblandad i. Där användes parametrarna S och M för att bestämma förhållandet mellan styvheter och massor. För "maximalt flat" återgivning varierades S och M för olika Q. Vid Q=0,383 blev S=1,414 och jag vill minnas att man fick ut Vb genom Vas/S. Vid Q=0,3 blev S=2 och lådan blev således mindre och vice versa för högre Q. Rippel var inte möjligt att undvika vid Q>0,383.

Vill minnas att formlerna refererades till Lea & Lampton men var de härlett sambanden ifrån vet jag inte men man kan väl gissa på T&S.

/Jocke

[Svante]

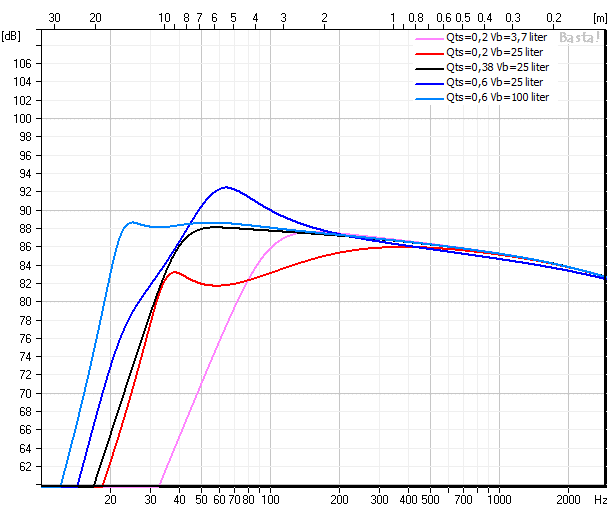
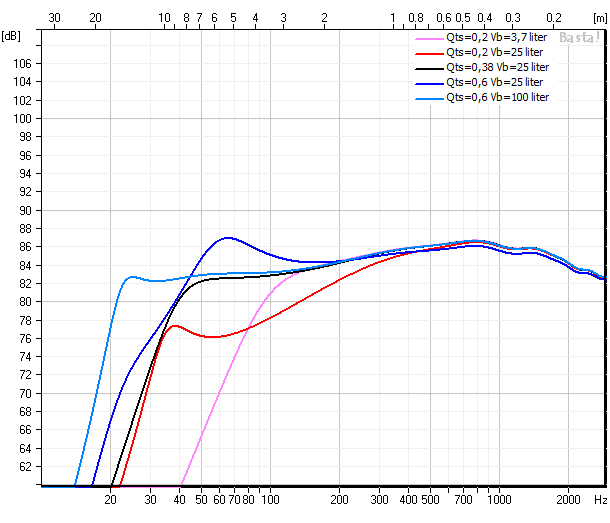
En gång i tiden lyckades jag lära mig lite av de här sambanden genom ett kompendium som "McBruce" (nick) var inblandad i. Där användes parametrarna S och M för att bestämma förhållandet mellan styvheter och massor. För "maximalt flat" återgivning varierades S och M för olika Q. Vid Q=0,383 blev S=1,414 och jag vill minnas att man fick ut Vb genom Vas/S. Vid Q=0,3 blev S=2 och lådan blev således mindre och vice versa för högre Q. Rippel var inte möjligt att undvika vid Q>0,383.

Vill minnas att formlerna refererades till Lea & Lampton men var de härlett sambanden ifrån vet jag inte men man kan väl gissa på T&S.

/Jocke

Man kan göra det ur överföringsfunktionen för basreflexlådan. Man har fem parametrar som bestämmer tre koefficienter i ett normerat fjärdegradspolynom. De fem parametrarna är fs/fh, Vas/Vb, Qts och två Q-värden som bestämmer resistiva förluster i låda respektive port.

Vid förlustfri låda och port ska Vas/Vb vara 1,41, fs/fh=1 och Qts=0.383 om det ska bli ett butterworthpolynom. Med förluster i port och låda Ska Qts vara större, Vas/Vb mindre och fs/fh ungefär samma. Man kan göra samma övning med chebychevpolynom också.

Det trista med den här metoden är att det finns flera saker som inte finns med i modellen som baffelsteg och rumseffekter. Ska man ha med dem så blir den analytiska matten för jobbig och man får simulera i stället. Det är å andra sidan ganska lätt, numera .

[Jocke]

Ja, jag har hört talas om ett program som heter Basta där man kan simulera alla möjliga förutsättningar - har du provat det?

Man kan ju då undra om baffelsteg och rumseffekter är olika för element med olika Q? Annars verkar det ju ju vara en teori som är möjlig att tillämpa på basåtergivning fortfarande.

Men visst har det blivit otroligt mycket enklare sedan jag körde de här beräkningarna på en Nord100!

/Jocke

[Svante]

Ja, jag har hört talas om ett program som heter Basta där man kan simulera alla möjliga förutsättningar - har du provat det?

Ja, det ska du låta bli, det är bara sopor.

Man kan ju då undra om baffelsteg och rumseffekter är olika för element med olika Q? Annars verkar det ju ju vara en teori som är möjlig att tillämpa på basåtergivning fortfarande.

Nej de är inte olika, däremot kan de bitvis samverka eller ta ut varandra. Om tex målet är en rak tonkurva, så kan ett lite högre Q-värde motverka obalansen mellan låga och höga frekvenser som uppstår pga baffelsteget.

[Jocke]

Ja, jag har hört talas om ett program som heter Basta där man kan simulera alla möjliga förutsättningar - har du provat det?

Ja, det ska du låta bli, det är bara sopor.

Det du vill höra är väl att det inte alls är så och att programmet är bra?

- Så är det inte, Svante! Pragrammet är utmärkt!

Man kan ju då undra om baffelsteg och rumseffekter är olika för element med olika Q? Annars verkar det ju ju vara en teori som är möjlig att tillämpa på basåtergivning fortfarande.

Nej de är inte olika, däremot kan de bitvis samverka eller ta ut varandra. Om tex målet är en rak tonkurva, så kan ett lite högre Q-värde motverka obalansen mellan låga och höga frekvenser som uppstår pga baffelsteget.

Var det inte det som Zaph hade upptäkt nu? Det var på tiden!

/J

[Kaffekoppen]

Är det där något nytt egentligen ?

Alltså att ett element som har högt q får en puckel i responsen och att den kan försvinna/mildras om man planerar baffelbredden lite? Känns ju inte särdeles revolutionerande direkt.

Har jag missat nått vässentligt?

[celef]

nu svamlar ni väl i nattmössan, inte kan man peaka basen med högt qt för att fylla ut för baffelsteget, det syns ju tydligt i simuleringen. eller kan man bredbanda portens bidrag numer?

[IngOehman]

Till att börja med vill jag säga att det är självklart att Q-värden över 0,7 kan vara försvarbara i många sammanhang.

Sen vill jag säga att man inte bör förenkla verkligheten till att bara handla om "rak tonkurva", men att det nog är vanligare att folk gör det motsatta - det vill säga nojjar in på andra mindre relevata saker.

Till sist vill jag säga att det blir väldigt konstigt att tala om ETT Q-värde när man diskuterar basreflexlådor. Det är system som approximerar fjärde odrningens system hyggligt nära, och det betyder att deras HP-funktion (helt oräknat effekter av baffeln, det vill säga baffelsteget) besrkivs av TVÅ polpar, inte av ett. Överföringsfunktionen beskrivs därför av två olika Q-värden, och att bara tala om det ena blir väldigt fel, för att inte säga irrelevant.

När det gäller slutna lådor är man närmare sanningen om man föreknlar verkligheten till bara en resonans/ett Q-värde, men inte heller då är det sant. Man ser nämligen nästan undantagslöst effekter av ännu en resonans som yttrar sig över gränsen mellan den mekaniska och de elektriska världen - resonansen mellan talspoleinduktansen och den övertransformerade membranmassan.

Sen finns det ju roliga saker som tredje ordningens slutna lådor också (som brukar kräva Q-värden för Fsl om 1 - 1,2 för att spela riktigt bra) som klarar att nå en F(-3dB) långt under Fsl, men det får vi ta nästa gång.


Vh, iö

- - - - -

PS. Fsl i texten ovan är den resonansfrekvens som bildas när ett högtalarelement placeras i en sluten låda. Det vill säga elementets resonansfrekvens gånger sqr((Vas/v+1). Där V förstås är lådans akustiska volym och inte den mekaniska.

[Kaffekoppen]

Är det där något nytt egentligen ?

Alltså att ett element som har högt q får en puckel i responsen och att den kan försvinna/mildras om man planerar baffelbredden lite? Känns ju inte särdeles revolutionerande direkt.

Har jag missat nått vässentligt?

Sluten låda håller jag mig till

[Svante]

Till sist vill jag säga att det blir väldigt konstigt att tala om ETT Q-värde när man diskuterar basreflexlådor. Det är system som approximerar fjärde odrningens system hyggligt nära, och det betyder att deras HP-funktion (helt oräknat effekter av baffeln, det vill säga baffelsteget) besrkivs av TVÅ polpar, inte av ett. Överföringsfunktionen beskrivs därför av två olika Q-värden, och att bara tala om det ena blir väldigt fel, för att inte säga irrelevant.

Mja, jag tror Q-värdet som diskuterades var elementets Qts-värde och vad man kan uppnå med olika sådana. Det värdet är ju inget av de två som du nämner, men påverkar båda. Som jag skrev så är tre av de där fem parametrarna Q-värden.

[Jocke]

Jag gillar verkligen tumregler i vanliga fall! Det beror så klart på att jag inte är så påläst att jag kan bortse från dem! Men här är jag beredd att hålla med dig, Ingvar!

Ofta avfärdas sådana här element här som oanvändbara när frågan borde vara hur man ska applicera en lämplig lösning!

/J

[celef]

kan nån säga om ebp-faktorn har nån relevans för att välja slutet eller portat system?

[Jocke]

ebp?

Är det den där beräkningen av parametrar som blir runt 100 för att "passa" i portat system?

/J

[celef]

ja just det, efficiency bandwidth product

ebp = fs / qes

ebp runt 50 lämpligt för slutet
ebp runt 100 lämpligt för portat

finns det någon relevans?