Hej Johan!
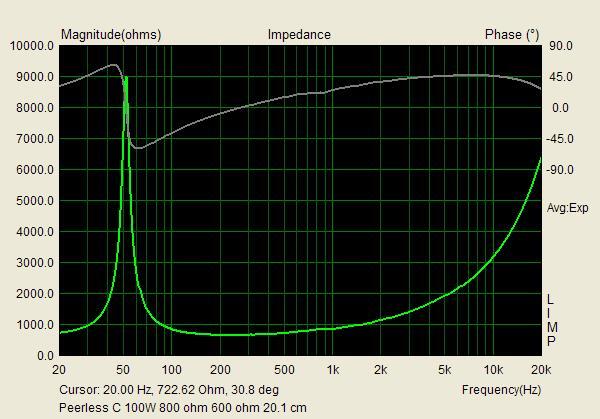
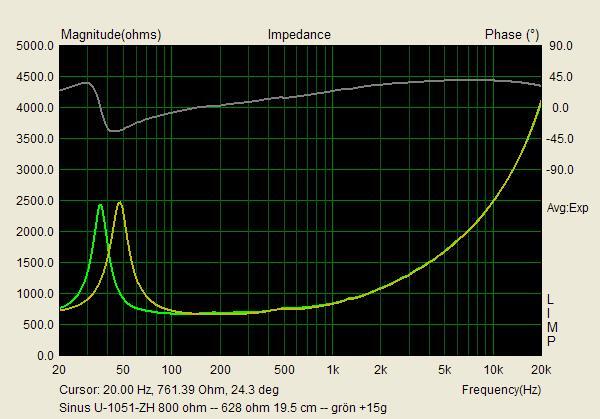
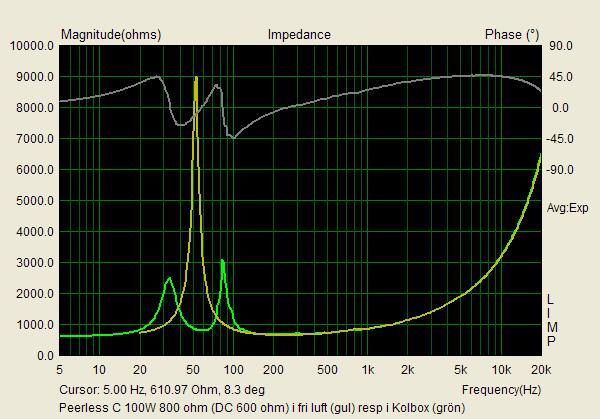
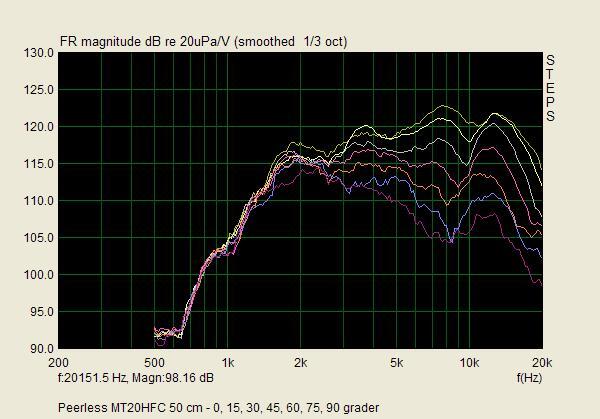
Jaha, det var ju jätteintressant. Pudelns kärna, skulle man kunna säga. För baselementet är ju vad som verkligen samarbetar med Kolboxens storlek och form. Jag har studerat dina T/S-mätningar, och de verkar ju kunna stämma, trots att troligen ingen använt programmet till 800 ohms element. Peerless verkar ju vara ett element i den äldre traditionen, som Philips 9710 med en lätt kon.
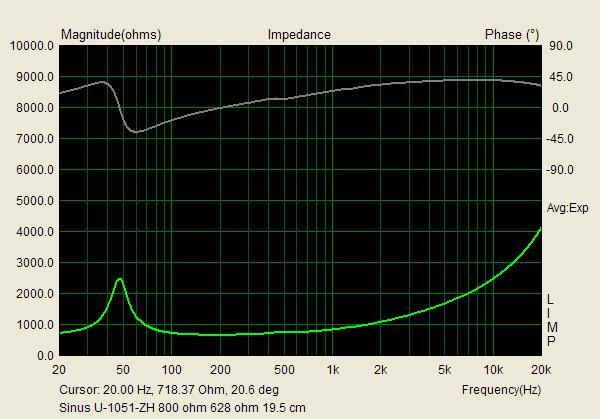
F.ö. har 800-ohm-elementen inte 100 ggr så många varv. Det räcker med 10 ggr så många som i ett 8 ohms element; om koppartråden har 31,6% av diametern blir som bekant dess area 1/10 och rho*l/A ger precis en faktor 100 vid ungefär samma dimensioner och vikt på talspolen som hos ett 8 ohms element. Så det där med 40 um tunn tråd verkar ganska extremt, men det har funnits 150 och 800 ohms högtalare i mindre format också. DC-resistansen på 600 ohm är också korrekt (jag har köpt
en sån här och den har också det); den är ju 5-7 på ett 8 ohms element. T/S skiljer sig ju helt klart med en faktor, som är i storlektordningen 10 jämfört med motsvarande 8-ohms element, såvida en spänning eller ström ingår (och alltså 100 om båda ingår, som hos impedansen!). Men att det är exakt 10, ska man kanske inte ge sig attan på, för den tunnare tråden lär ju i proportion ha haft ett tjockare lackckikt, som kanske givit lägre verkningsgrad.
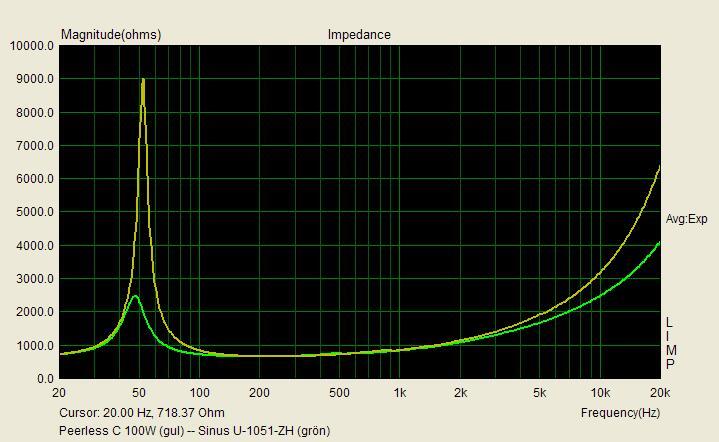
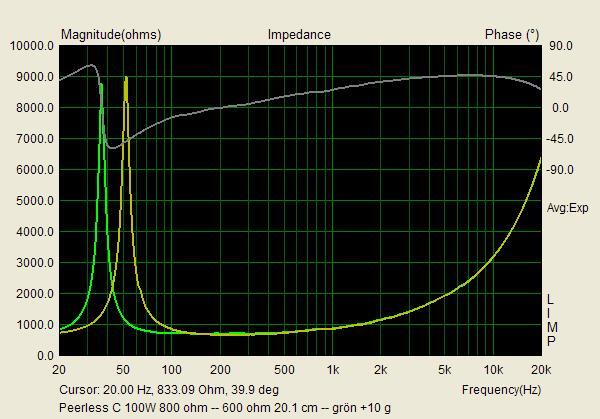
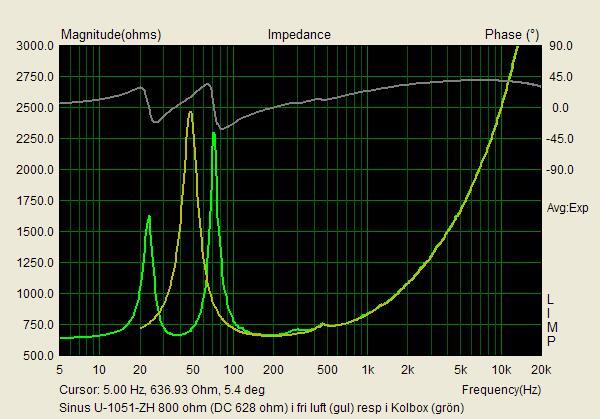
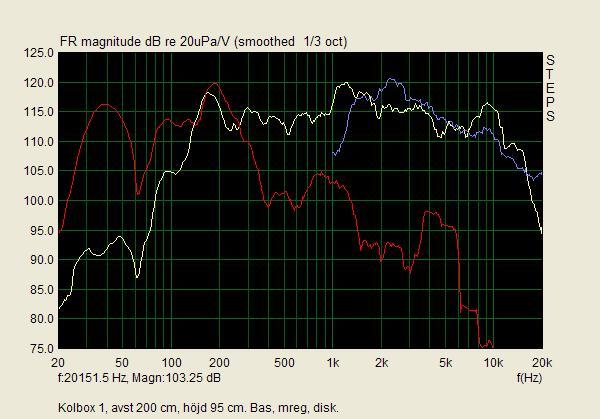
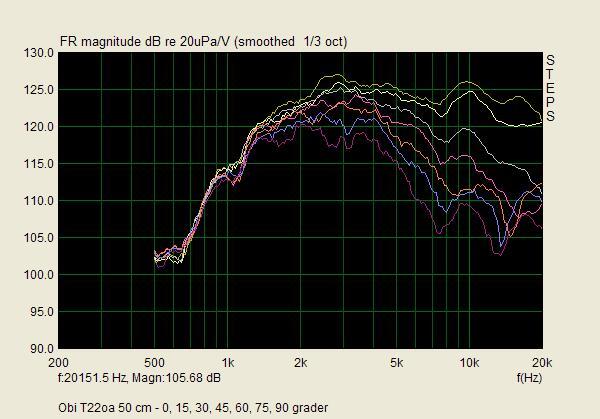
Det som förbryllar mig är bara varför avstämningen skiljer mellan de båda exemplaren. Carlssonplanet talar ju i sin historieskrivning om att det var Peerless som gällde för Kolboxen och att Sinuselementet utvecklades för den senare m.h.t. till industriell tillverkning utvecklade OA-6. Elementet på skissen är ju också likt Peerless, om man tar det för vad det är, nämligen en skiss, som inte ska förråda industrihemligheter. Och din logiska förmodan är ju att din Sinus satts in efteråt såsom senare tillgänglig reservdel, tyvärr med den misshandel av bottnen, som det medfört. Varför i all sin dar har då lådan med Peerless en högre avstämning, ca 58 Hz, t.o.m högre än elementets friluftresonans på 52? Rimligen bör en basreflex enligt Carlssons patent vara underavstämd, liksom din Sinuslåda är, eftersom han ville ha en fallande kurva i basen till att kompensera vad som här på forat brukar kallas "rumsstödet". 36 Hz är visserligen svårt att avläsa på den flacka impedanskurvan, men man brukar ju ta Peter Åkemarks trick att definiera det som 0 grader på fasen i stället*.
Som jag nämnde i epost (till Johan alltså), har jag bara gjort grova överslagsberäkningar på schemat av Kolboxens rörförstärkare hittills. (SPICE-simuleringar har jag som IC-konstruktör haft nog av under 25 års jobb.) Det som inte stämmer alls är förstärkningens absolutvärde för båda kanalerna. Jag tror den borde vara 10 dB högre, om i mellan/diskant-kanalen återkopplingsmotståndet R17=27 kohm, som rättelsen för hand säger. Kanske har man ändrat skalan 10 dB för att försvåra industrispionaget något, eller inte observerat att den inte går från 0 dB! I databladet nämns ju något om 1 V ut från förförstärkaren Lund 1001, och uppemot 100 V ut från slutsteget måste man ha, för att få 12 W i en 800 ohms högtalare ... Och baskurvan borde gälla vid inkopplad högtalare, där den positiva återkopplingen (för negativ utgångsresistans) ger kanske 6 dB högre utspänning än tomgångsspänningen. (Om kurvan gäller med omkopplaren i det visade läget med minimal basförstärkning.) Alltså måste baselementet, som jag alltså inte känner annat än genom din beskrivning, vara ännu känsligare än den välbekant högkänsliga 9710, om reflexerna från golv och väggar ger en förstärkning på c:a 7,5 dB vid 500 Hz. För övergångsfrekvensen är i denna storleksordning och inte alls där de båda kurvorna skär varandra vid knappt 200 Hz! För baskanalen skulle jag tro att den (bestämd av C16) ligger vid 450 Hz för 800 ohm i högtalaren eller 540 Hz vid 600 ohm. För mellan/diskant-kanalen tycker man sig se -3 dB vid 500 Hz jämfört med platån vid 2 kHz. Det kan nog stämma, för den har två poler, 0,159/R17/C10=236 Hz och 0,159/R19/C11=170 Hz. Det syns inte tydligt, då man inte dragit diskantkurvan längre ner i frekvens och kurvan trots den lustiga skalan - linjär mellan 0 och 100 Hz(!) - rimligen borde ha lutat mer än 6 dB mellan 50 och 100, detta trots det obetydande nollstället vid 0,159/R6/C10=6 Hz. Resten av diskantkurvan stämmer rätt bra, alltså "i grunden" en sluten slingförstärkning på 80x eller 38 dB, ett nollställe vid 0,159/(R15||R17)/C9=8,6 kHz och en pol vid icke för någon hörbara 0,159/R15/C9=32 kHz.
Mitt första ordningens förslag till delningsfilter är alltså dessa hörnfrekvenser, medan dalen vid 80 Hz ser ut att komma helt från den negativa utgångsresistansen -R51*(R32/R33)=-416 ohm i kombination med den "slutna resonansens" impedanstopp hos elementet! Utgångsspänningen
stiger ju, när belastningen minskar! "Mellanfrekventa" förstärkningen hos baskanalen uppskattar jag till 28x eller 29 dB. Det är fortfarande litet för en 800-ohmare med nominellt 1 V från försteget (men för 8 ohm är skaleringen inte heller gjord!). Du bör alltså inte ha någon svårighet att ställa in ett parametriskt aktivt delningsfilter enligt detta. Vad jag ännu inte analyserat är korrektionen vid (eller under) avstämningsfrekvensen. Den kommer som synes från en "notch"-krets i återkopplingen, som torde vara väldigt känslig för komponenttoleranser. (Det var 10% massamostånd som var standrad vid den här tiden, men det anges ju till skillnad från Idestam-Almquist inga toleranser i stycklistan!) Att ha en topp på 20 dB vid 35 Hz tycker jag verkar häftigt. Men där kan anhängarna av "Linkwitz-transform" och liknande ge dig bättre råd; de använder ju t.o.m. samma förstärkning ner till DC!!!
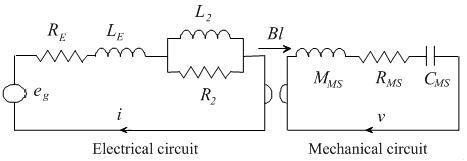
*=Det är inte exakt samma frekvens man då definierar! (Med risk för att jag får en släng av sleven av "IÖ", för att jag fuskat på hans revir som överlärare på forat, erkänner jag ändå att jag försökt förklara admittansanalogin i den här tråden. Men det handlade om det grundläggande faktum att det blir "kamelpucklar" på impedanskurvan ...) Jag tänker så här i admittansanalogin - se tråden ovan; i den här diskussionen försummar jag talspoleinduktansen vid basfrekvenser: Admittansen Yms blir då induktiv vid låga och kapacitiv höga frekvenser, men har alltid en (positiv) realdel som bestämms av den mekaniska dämpningen. Vid systemresonansen i luft, fs, är admittansen minimal och reell, det gäller exakt. Vid ett frekvenssvep rör sig orten för admittansen nerifrån (negativ imaginärdel) och upp på en rät linje. Men när låda och port tillkommer, får vi i admittansschemat en seriekrets Lab+Cbr adderad. Seriekretsens impedans rör sig också på en rät linje, så när vi inverterar den till en admittans, får vi en cirkel - positiv imaginärdel för låga frekvenser och negativ för höga. Cirkeln genomlöps alltså medurs. Om nu helmholzresonansen, fb, har någorlunda högt Q-värde kommer följande att hända vid ett frekvenssvep: Först går vi "uppåt" på vår räta linje och adderar en cirkel, där vi fortfarande befinner oss nära dess startpunt, till vänster. Med stigande frekvens händer först inte så mycket längs cirkelbågen, men cirkeln förflyttas uppåt med Yms. När vi närmar oss fb, går vi snabbt längs cirkeln, för att få ett maximalt (och rellt) admittansbidrag vid fb. Jag antar att lådan är underavstämd, d.v.s. fb < fs. Då har vi redan passerat den frekvens där totala admittansen är rent reell, fr. D.v.s. elementets fortfarande induktiva susceptans kompenseras av lådans kapcitiva. Men vi får gå något litet högre i frekvens än fb för att hitta den punkt som är längst från origo, alltså admittansmaximat eller impedansminimat, säg fm. Denna punkt har ju en något mer negativ imaginärdel än cirkelns mitt. För en underavstämd låda, alltså fb < fs, gäller alltså fr < fb < fm ("ungefär lika med" skulle man kunna säga i den sista olikheten). Omvänt gäller naturligtvis för en överavstämd låda. Jag ser det i båda fallen som att fm dras något litet från fr mot fs, om inte fb's Q-värde är väldigt högt. (Och det är det inte alltid, snarare 2 än 7 för en OA-5!)Om det är någon här som jag inte har förolämpat i kväll, så ber jag denne om ursäkt. (J. Brahms)