Svante skrev:IngOehman skrev:Svante skrev:Jodå jag vet. Jag bara läste Ingvars inlägg lite fort och hittade mer och mer i det när jag läste om det.
Inget problem alls. Tack för svaren.
Är dock fortfarande inte på det klara riktigt med vad det är du testar.
Att det kan bli problem i den apparat som man spelar upp musiken i är ju en sak, och visst kan
tillverkarna ta till lite för dålig marginal därvidlag således att sinc-vindlingarna/vågningen som
uppstår då man översamplar kan rendera klippning. men då är ju ändå de signaler som finns på
fonogrammet icke-nyquist-fientliga. Men det kanske de som du talar om uppfyller också.
Jag är inte säker på att jag helt förstod ditt svar med avseende på just detta.
Är i själva verket inte ens säker på att jag förstår om en signal i den digitala domänen KAN vara
nyquist-fientlig. Fast jag själv resonerade om det.
Hmm... Kan ett antal samples i den lagrade koden vara "omöjlig" i betydelsen att det inte finns
någon analog insignal som kan resultera i den, utan att innehålla energi över Fs/2?
- - -
Jag tycker att jag borde veta svaret på frågan intuitivt, men det är inte så lätt efter all påskmust
som de andra druckit, så jag slapp och fick vin istället. Att fundera går bra, men att komma fram
till något är inte lika lätt.

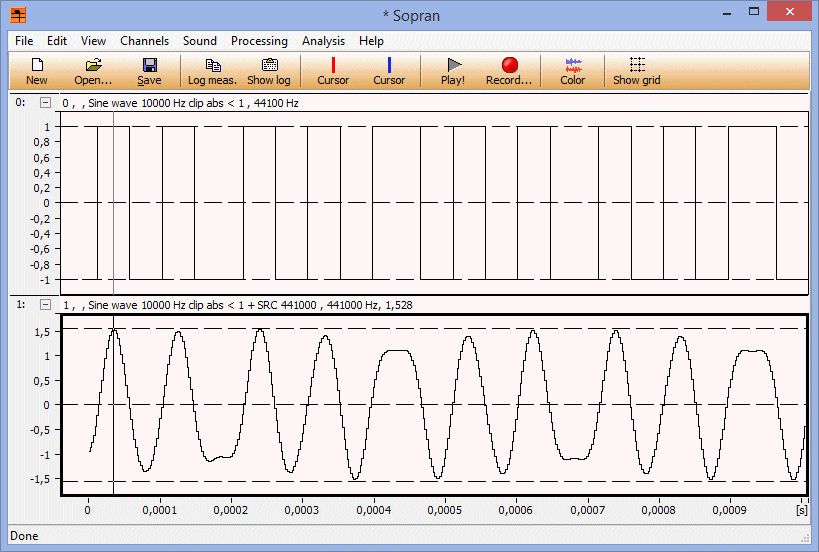
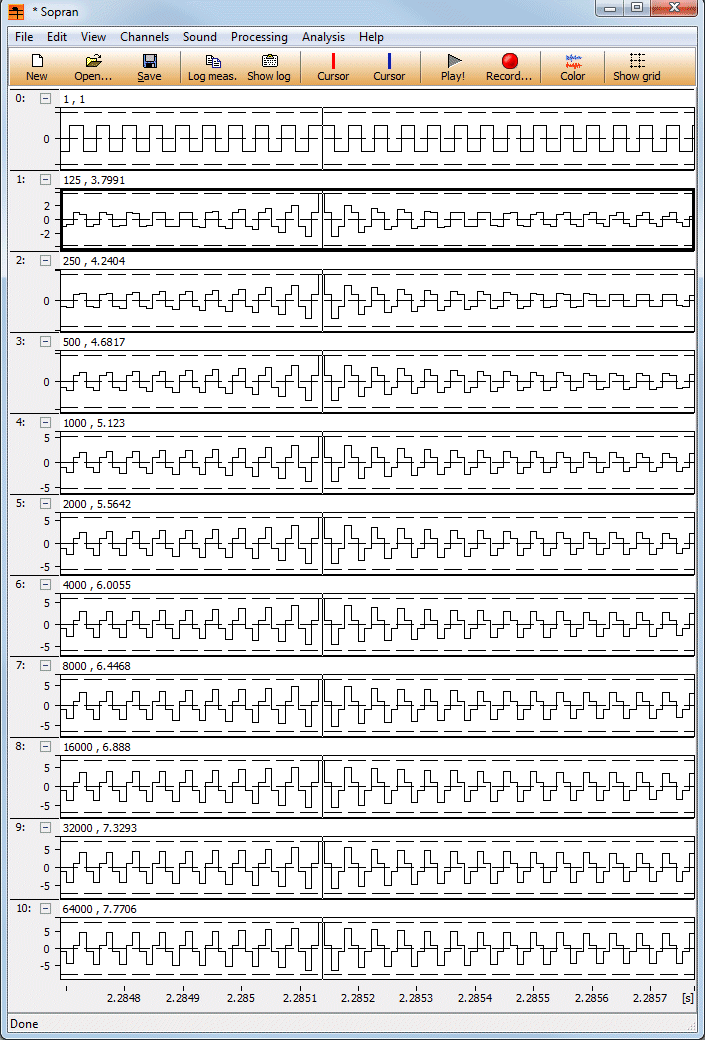
Får en sorts dejavu (eller hur det stavas) och associerar när jag ser dina fasvingliga fyrkantvågor
till strömförbrukningen som kan uppstå dynamiskt när man har en högtalare med reaktiv impedans.
Det är även där lätt att visa att man kan få toppströmmar mycket större än Uinmax/Zmin, men det
är också svårt att beräkna den teoretiska gränsen för hur stora toppströmmar som kan uppstå med
en insignal som är helt formfri och bara begränsad med avseende på max spänning åt både plus-
och minushållet.
Har en känsla av att det finns släktskap matematiskt, även om det är olika funktioner som "kopplar
samman" orsakande och resulterande signal, nämligen sinX/X respektive högtalarens impedans.
Vh, iö
Hmm, nuskavise om jag kan uttrycka mig bättre.
Alltså jag försöker hitta en digital signal som är sådan att den efter uppsampling ger så högt toppvärde som möjligt. Som du säger kan inte en digital signal vara nyqvistvidrig, signalen innehåller ju per (den vanligaste) definition(en) endast frekvenser under fs/2. Jag tänkte mig närmast att om man klipper en signal i den digitala domänen så bildas det övertoner, men eftersom de inte kan ligga över fs/2 så viks de ner under fs/2.
Så signalen jag har är alltså helt syntetisk, det finns nog en analog signal som man skulle kunna sampla så att den blir som min digitala signal, men det har jag inte brytt mig om.
Jag tror du kan stryka "nog". Svaret på frågan är ju att den finns, nämligen samma signal som den du får
ut ur din uppsamplare!

(Finns det förresten något speciellt skäl till att du skriver uppsampling istället
för översampling?)
Men (och detta är ett lite viktigt men kan jag tycka) om du skulle skapa en analog signal av detta slag
och sampla den (AD-omvandla) så känns det inte troligt att de platta klippliknande vågformstaken skulle
hamna på den höga nivå som man kan få dem när man klipper digitalt.
Teoretiskt är det förstås möjligt att så skulle bli fallet om head room för ingångsförstärkaren är tillräcklig
och man har sådan osannolik "tur" att samplen hamnar på exakt rätt ställe, men om man har ett utstyr-
ningsinstrument som läser den analoga insignalens peaknivåer så skulle man ändå klara sig.
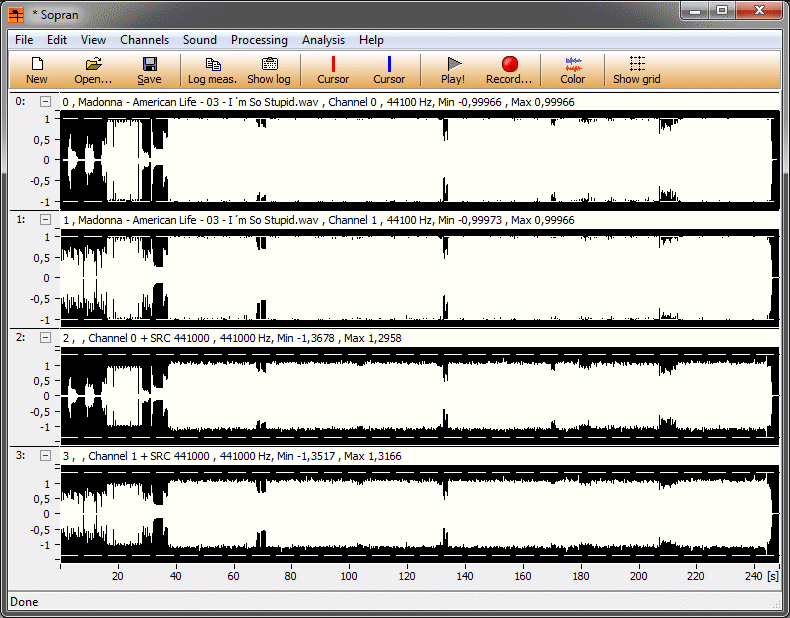
På något sätt känns det som om dina studier (som är mycket intressanta) framförallt är av betydelse för
dem som är intresserad av vilka problem som kan uppstå när några är framme och maximerar signalen i
den digitala domänen, det vill säga mastrar...
Så länge man nöjer sig med att spela in och mixa musik och kanske komprimera i den analoga domänen
föra ADC så torde problemet, eller rättare sagt risken för att problemet skall uppstå, vara minimalt.
Svante skrev:Jag känner mig i stället väldigt artistisk och fri och skapar signalen som jag vill i den digitala domänen.
Och det gör du förstås rätt i när det är vad som kan hända när man gör så som du studerar. Och som jag
ser det så är det absolut meningsfullt att titta på sådana saker, inte bara som ren grundforskning utan
som en studie specifikt inriktad på att finna vad som kan gå snett i mastringsstudiorna, det vill säga med
fonogrammen när de modifieras i mastringsttudierna.
Svante skrev:I varje fall kan signalen rekonstrueras till en analog bandbegränsad signal, möjligen med reservationen att amplutuden måste vara oändlig i en punkt. Hmm...
Min känsla är att amplituden inte kan bli oändlig, eftersom sincens vindlingars sammanlagda amplitudtid-
produkt inte går mot oändligheten ens om man integrerar från minus oändligheten till plus oändligheten.
Men jag är inte säker.
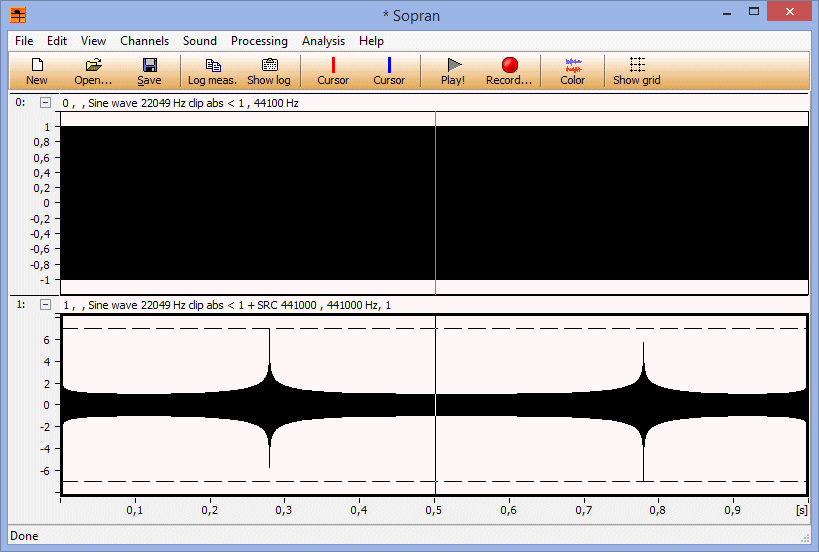
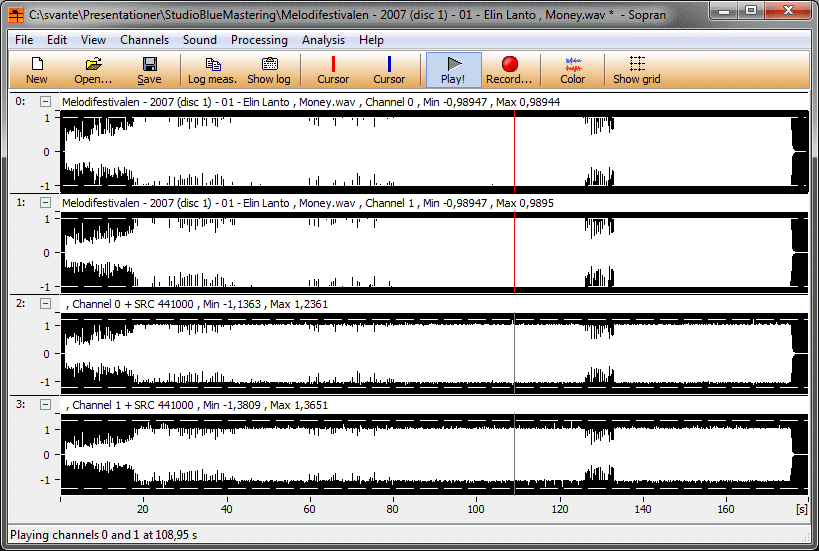
Svante skrev:...men den digitala signalen är alltså begränsad till +/-1 (=full utstyrning) och efter omsampling blev den mer än 10 dB starkare och jag tror mig ha visat att den kan bli hur stor som helst, givet ett idealt rekonstruktionsfilter.
Det beviset tror jag att jag har missat. Har du lust att repetera eller förtydliga dig? Jag har ju sett att du
genom att fortsätta leta har lyckats hitta högre och högre toppar, men det säger ju inte att limes per de-
finition blir oändligheten, det kan ju lika gärna vara ett ändligt tal, eller?
Svante skrev:Dessutom tar jag mig friheten att leka med rekonstruktionsfiltret, jag har ju skrivit uppsamplaren själv så då går ju det. Det visade sig att den vanliga inställningen, där jag inte har en riktig sinc, utan en som dämpas lite mer i svansarna, och som svänger lite långsammare än sincen ger mindre översläng än den nära ideala* långa trunkerade sincen med 20000 perioder.
En vars energi rullar av lite före 22 050 Hz alltså och inte är oändligt brant. Ja, det är ju lätt att förstå att
det blir så. Förenklar(kortar) man sincen till en rektangelstapel så blir ju överslängen noll.
Vh, iö
Fd psykoakustikforskare & ordf LTS. Nu akustiker m specialiteten
studiokontrollrum, hemmabiosar & musiklyssnrum. Även Ch. R&D
åt Carlsson och Guru, konsult åt andra + hobbyhögtalartillv (Ino).