Nu kommer första försöket med att skapa ett helt högtalarelement i FEM.
Jag kommer att fuska på en del punkter i detta första försök.
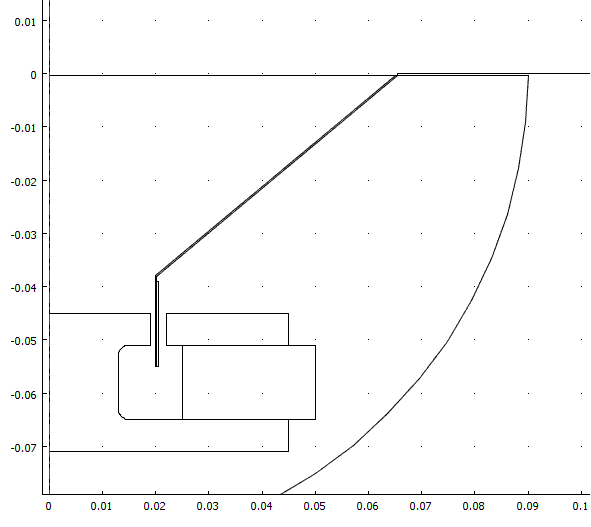
Först behövs ett magnetsystem - tillhör ett magnetostatiskt system.
Tre större fusk här -
1) Magneten ersätts med en magnet med 0 magnetisk utimpedans (reluktans) - en ideal B-fälts generator som sprutar ur sig 0.4 T helt enkelt. (Kan förbättras)
2) Det magnetiska ledningsystemet har en konstant permabilitet på 4000. Järnet mättas således inte DC mässigt. (Kan förbättras)
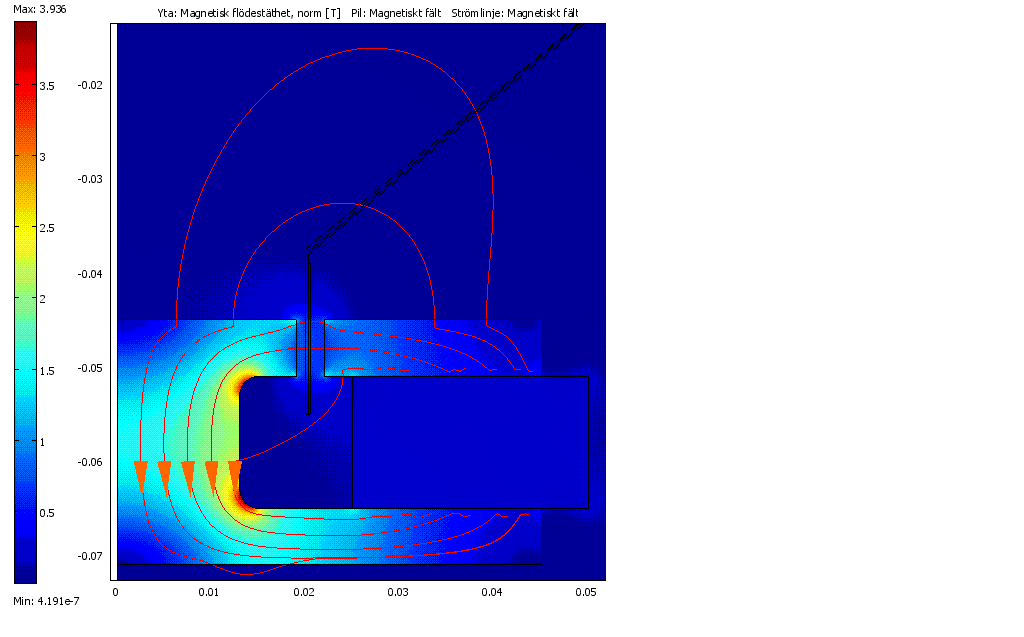
Allt över 1.5T i järnet är orimligt - det bör ha gått i mättning.
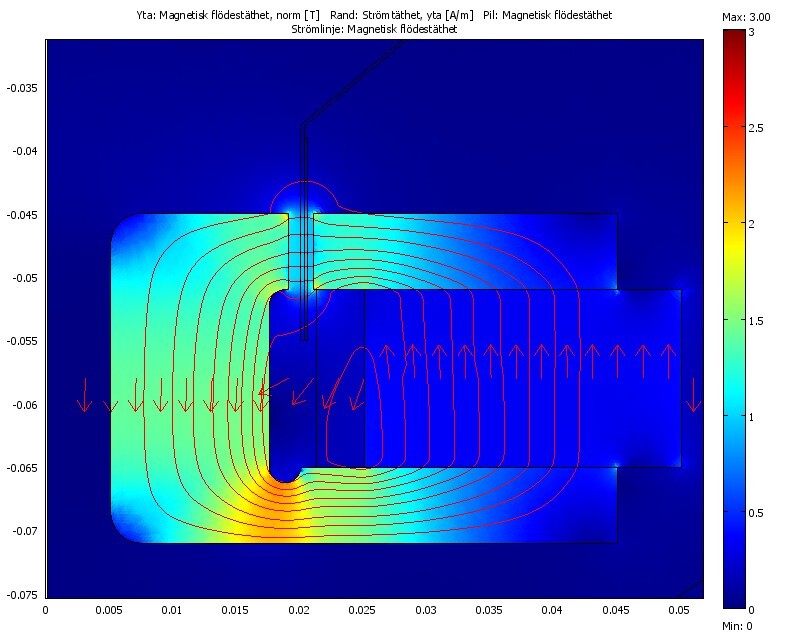
Nu kan vi beräkna B-fältet över spolen.
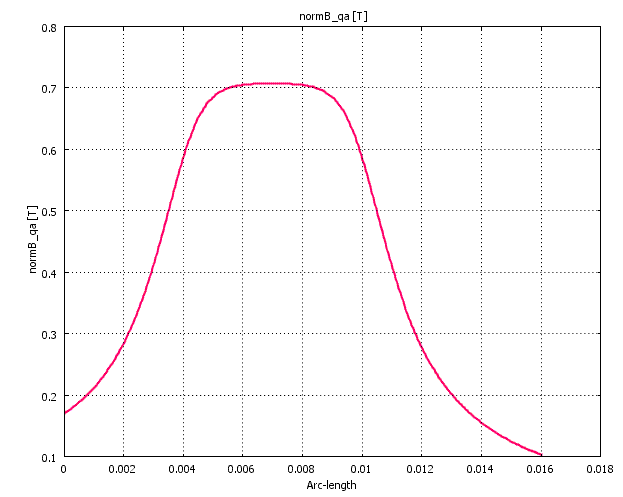
0.7T i gapet är ganska klent, ingen superhögtalare det här.
3) Spolen är def. som att den är lindad 100 varv med en viss tvärsnittsarea samt radie, och att den får en total DC-resistans på 6 ohm. Vilket inte alls behöver stämma överens med materialet koppar.
(Bättre att faktiskt linda en spole i koppar i FEM som får plats i gapet, men här fuskas det)
Det är då möjligt att räkna ut kostanten BL vid utslaget 0. BL blir ca 5.5 N/A.
Då var DC fallet klart.
*--------------------------------------------*
Nu ska AC fallet beräknas.
Spolen ska spänningsättas i magnetgapet med 2.83 V RMS, och induktansen inkl. förlusterna i magnetsystemet ska beräknas.
Opps, alltså spolen kommer inducera en ström i järnet som tillslut blir värme, vid 10 kHz är skinndjupet för järnet ca 20um! Jag har minne i min laptop för att göra en randmesh längs järnet på 15 um, så jag nöjer mig med den högsta ljudfrekvensen 8 kHz. Det problemet får 150 000 frihetsgrader.
(För att simuleringen ska vara meningfull bör jag ha i alla fall två trianglar per skindjup, trianglarna får sedan växa till storlek in i järnet.)
Allt detta slit för att beräkna spolens induktans, (som inte är kopplad till konen än)
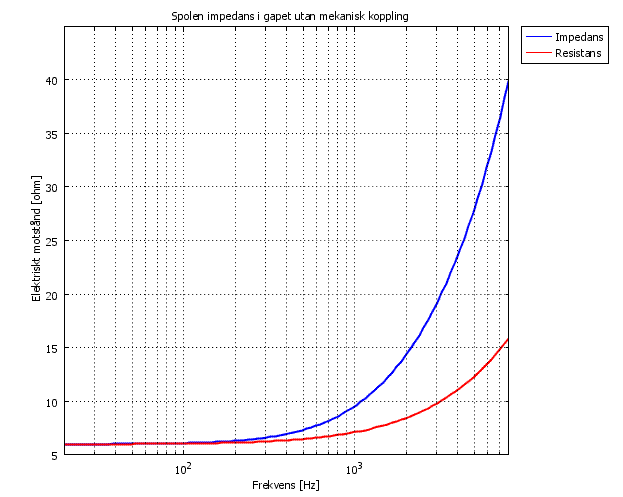
Se där!!! Resistansen är inte konstant, får en del förluster i järnet
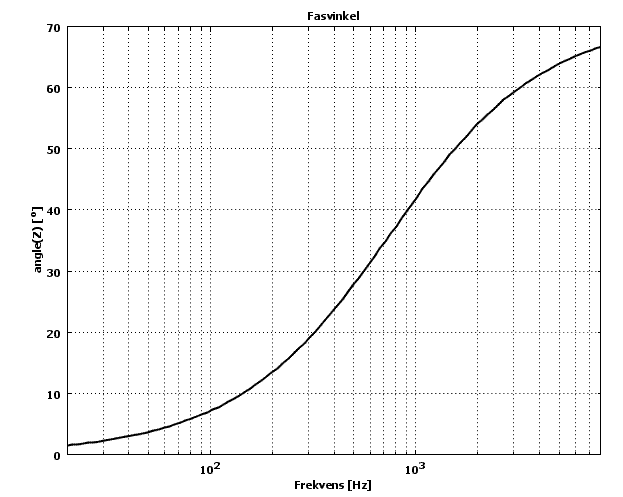
Ett annat sätt att undersöka fenomenet är att titta på fasvinkeln, en spole i fri luft ska få vinkeln 90 grader för höga frekvenser, men runt järn ska det bli mindre.
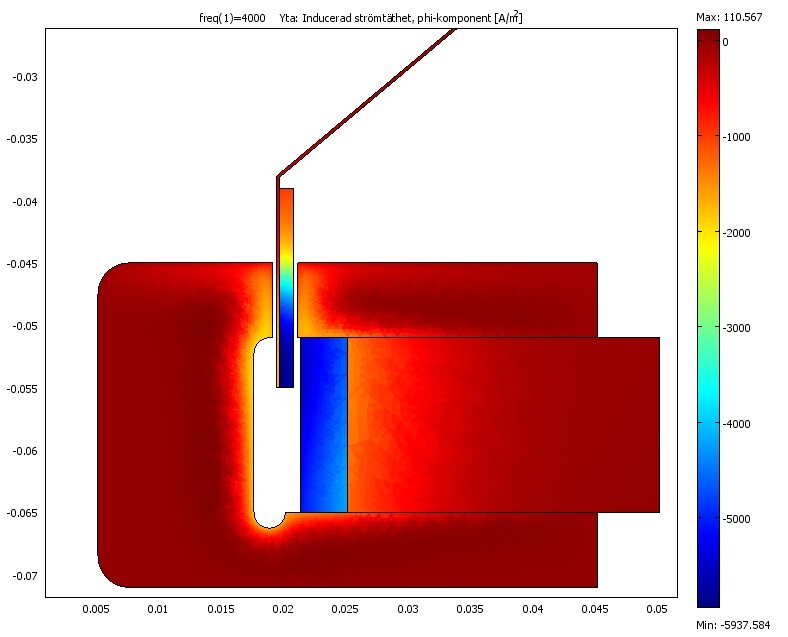
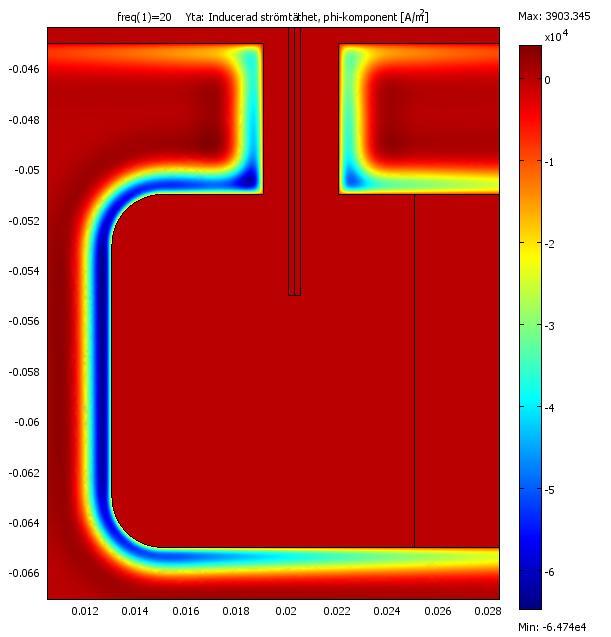
Så en titt hur den inducerade strömtätheten i järnet ser ut, först 20 Hz där skin djupet är ganska stort.
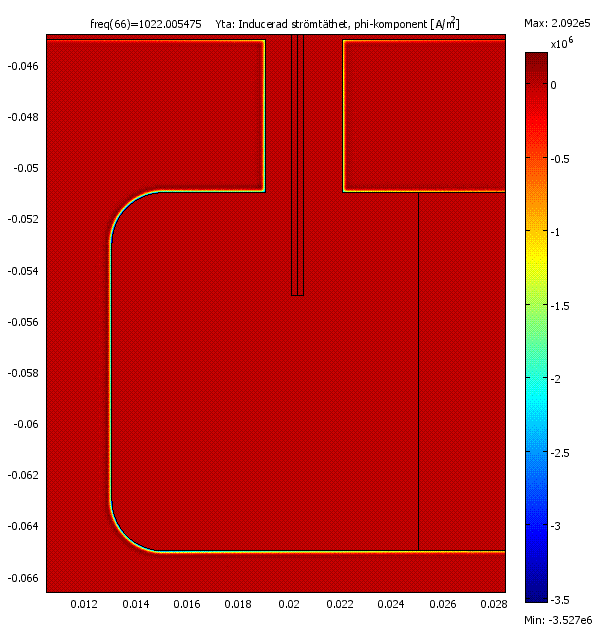
Men redan strax över 1000 Hz så är skin djupet mycket mindre, och strömtätheten börjar då bli riktigt stor.
*----------------------------------------------*
Nu till det mekansika.
Membranet får materialvalet magnesium, och spolen koppar. Spindeln och membranhättan utgår. Membranets ytterkant kopplas till en linjär fjäder med fjädringskonstanten 1.4e-3[m/N], samt lite mekanisk däpning 1.2[N*s/m].
Nu kopplas mekaniska påkänningar på konen in i fysiken. Spolen verkar i z-led på konens mitt, och fjädern verkar på konens ytterkant.
Detta gör att själva konen kan hamna i en mekaniska resonans, dvs få uppbrytningar. Konens totala mekaniska massa löser sig själv iom materialens densitet.
Lät det enkelt? Jag skrev inte mycket om mekaniken med konens uppbrytning ... men den finns där.
Så, på med akustiken.
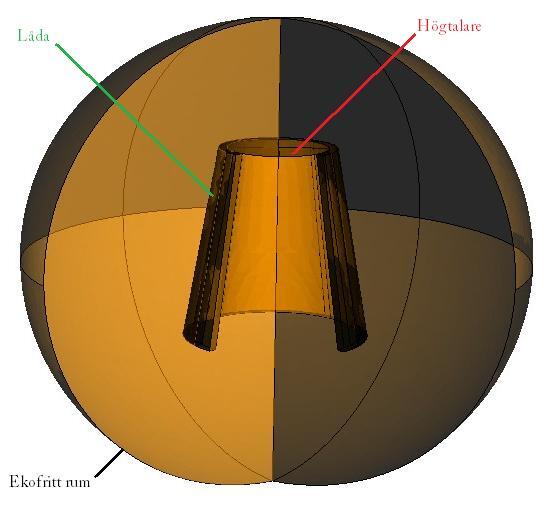
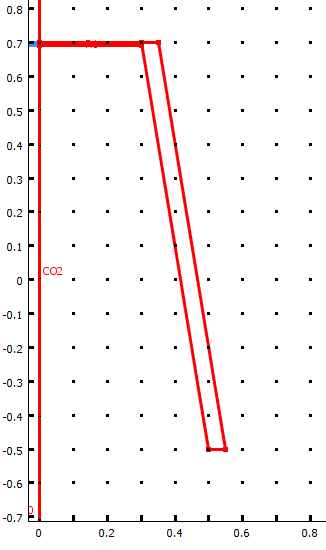
Accelerationen i varje punkt på konen ska nu kopplas till den akustiska domänen. Ett litet ekofritt rum skapas bakom högtalaren och en lite större halvrymd framför högtalaren.
Klent med RAM
Ni får nöja er med ganska få punkter just nu och bara upp till 3.5 kHz. Min Laptop...
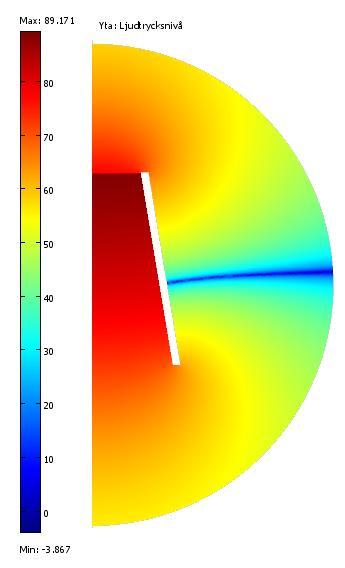
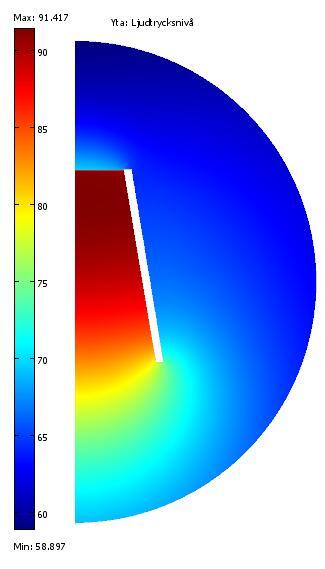
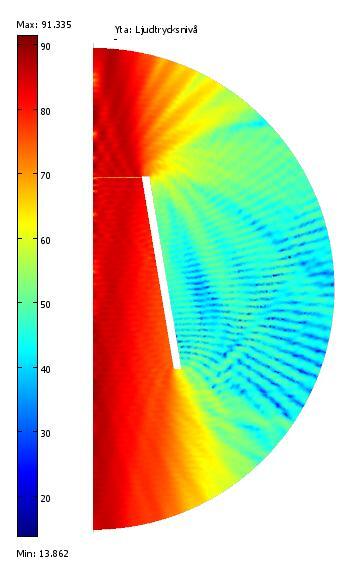
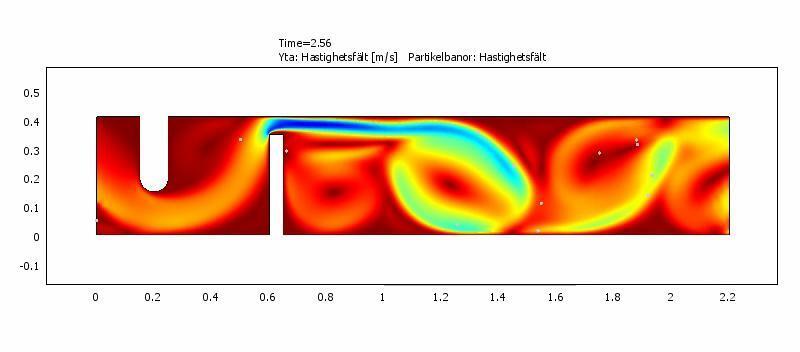
Hela uppställningen ser ut så här vid 2.83V in @ 3.5 kHz i den akustiska domänen.
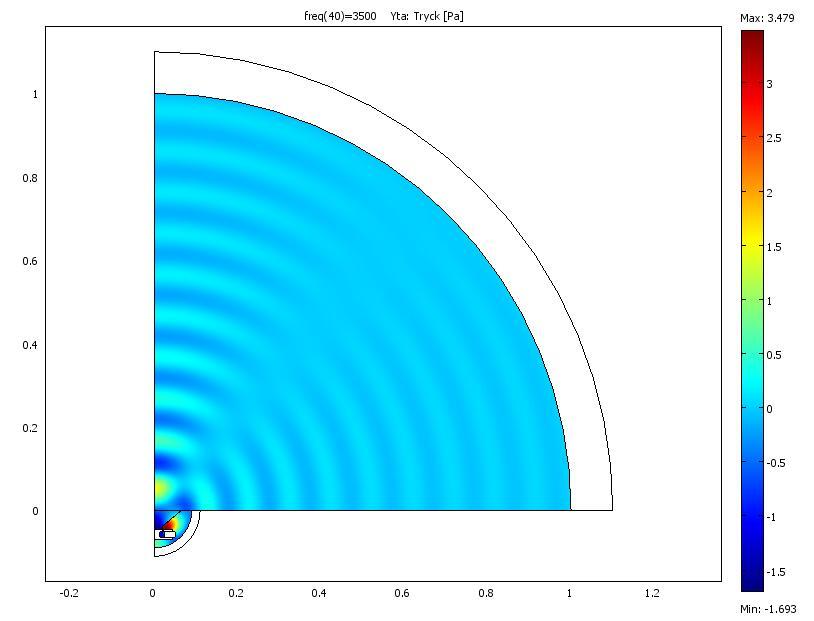
Den elektriska impedansen kopplad till det mekansika nu såhär.
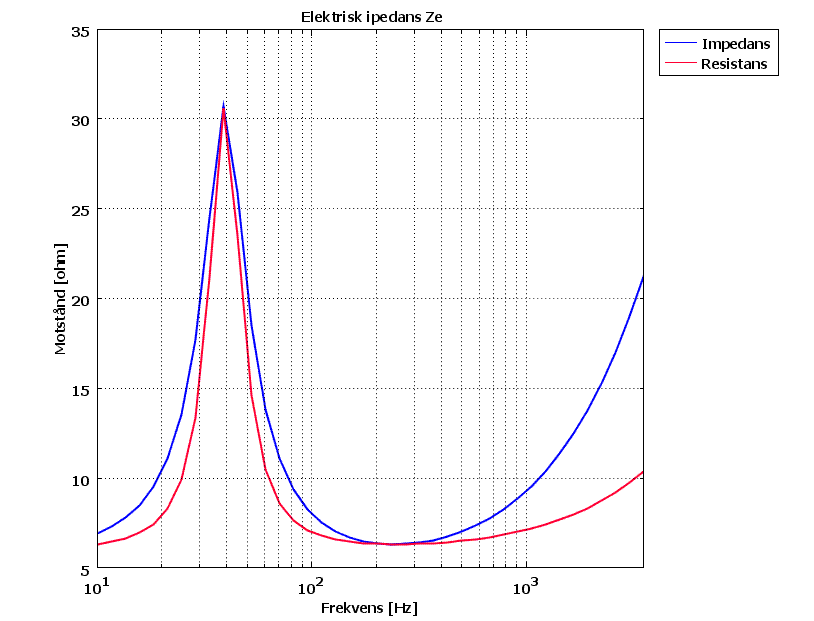
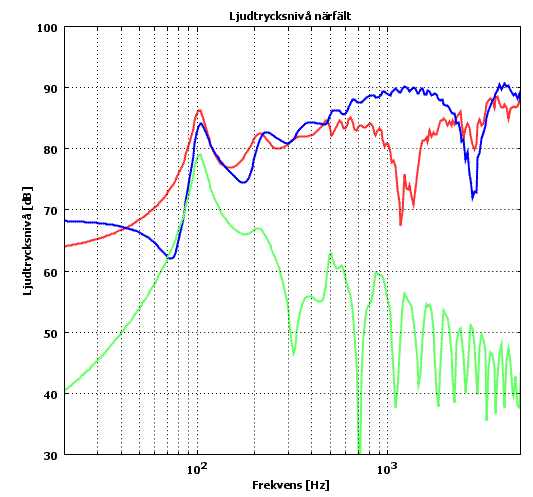
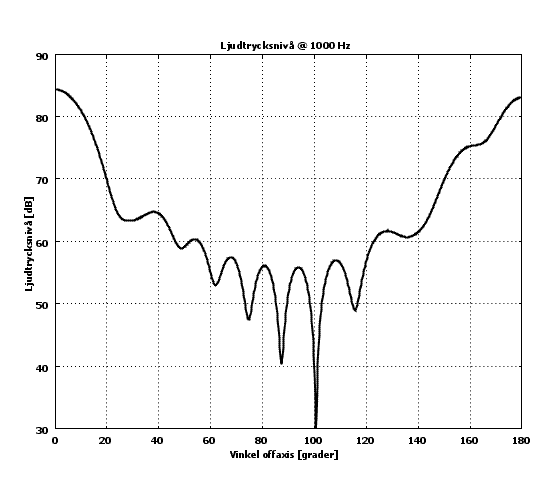
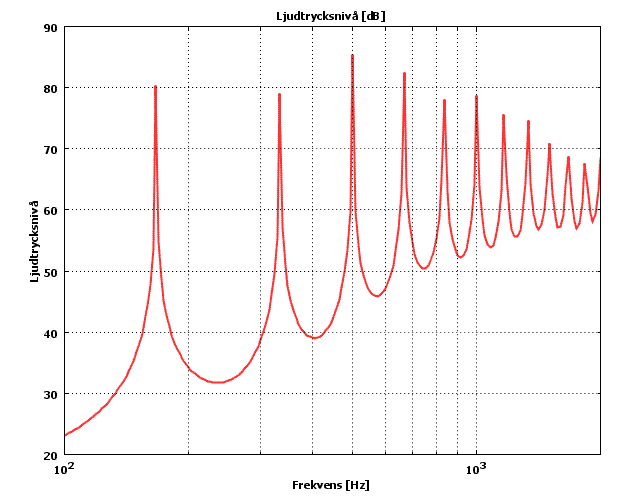
Och tillslut några tonkurvor
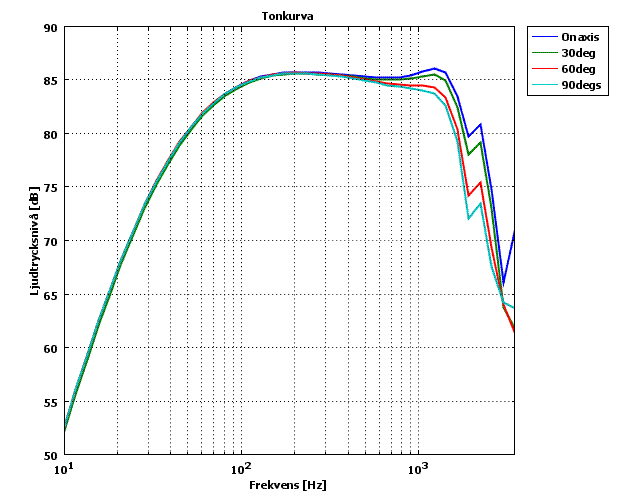
Undrar vad det där blev, jämföra med Basta
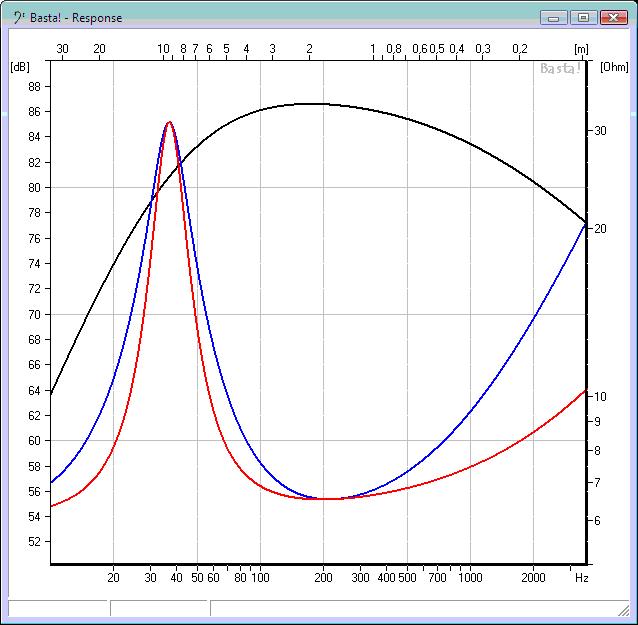
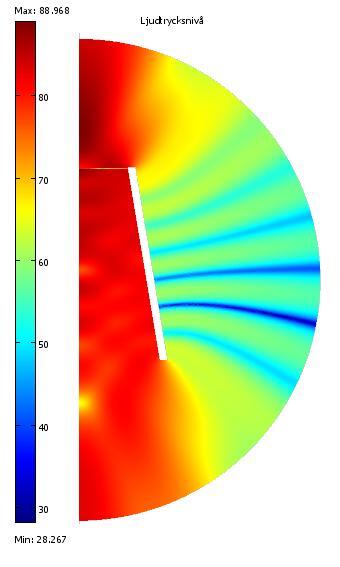
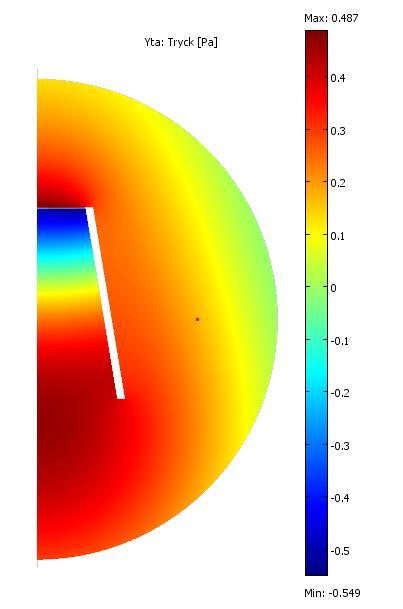
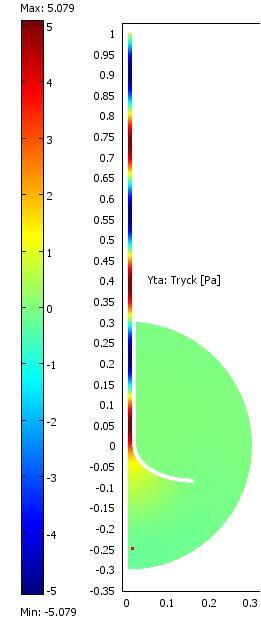
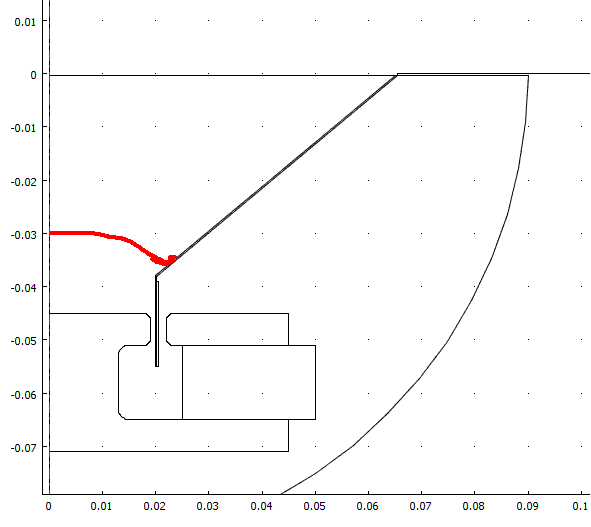
Nu vet jag vad som spökar! Kollar man på trycket vid 10 Hz så ser man att det läcker genom magnetsystemet till baksidan, jag har ju ingen hätta på högtalaren, dessutom har jag inga turbulenta flöden inkopplade, så det kan läcka förlustfritt från framsida till baksida. Det gör att det faller av i basen > 12 dB okt i min simulering. Så har ju jag med uppbrytningar också.
För att göra det lättare att förstå visas ljudtrycket istället för ljudnivån.
