hevi skrev:Svante skrev:Naquref skrev:Här ser man ju en komprimering. Men inte så stor som när det är oemotkopplat. Hur blir det då om det omvända råder? D v s om förstärkningen ökar med nivån?
Då får man en expansion på 25% oemotkopplat och 2.3% med motkoppling. (A=100 @ 1V, A=80 @ 0.1V)
Ponera att man lägger arbetspunkten så att man får en komprimering för för nivåer under nollan och en expansion för signaler över nollan. Då får man både en relativ komprimeringsminskning i det ena fallet och en relativ expansionminskning i det andra. Vilket kommer hörseln att bry sig om mest?
Eller tänker jag i galen tunna igen?

Ja, nu skulle jag väl inte kalla det för komprimering i första hand, lika lite som jag skulle kalla en distpedal till en elgitarr för kompressor. Icke desto mindre är det en dynamikreduktion, och som du säger är den mindre än i det omotkopplade fallet.
Om förstärkningen i stället ökar med amplituden blir det också som du säger, dvs att den expansion som uppstår minskar.
Fallet Naq nämner är väl i princip exakt det som man har i SET-fallet. Här är ett typiskt diagram för en triod och relationen gridspänning anodström (input är gridspänning och outputen är anodströmmen):
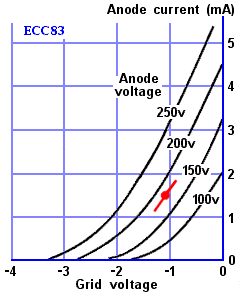
Arbetspunkten har man i det här fallet valt till ca -1V grid och 175V anodpänning (röda pricken) och svinget man avser utnyttja för sin SET är det röda lilla strecket. De svarta sträcken med olika spänningar som böjer sig över diagrammet är hur insignalen förhåller sig till utsignalen vid olika anodspänningar. Har man 200V anodspänning så kommer ingen ström flyta vid ca -2,7V. Vid -1V så flyter 2mA genom anoden.
Det som är intressant att notera här är dessa kurvor är "bananböjda". Även om dom ser rätt raka ut i det område som är markerat med rött så är dom böjda, dvs förhållandet mellan insignal och utsignal är inte linjärt.
Förutom att sambandet mellan insignal¤/utsignal inte är linjärt så är inte heler "böjningen" symmetrisk runt arbetspunkten. Precis som Naq's frågeställning så böjer kurvan mer under arbetspunkten och lite mindre över arbetspunkten vilket ger precis den effekt naq talar om.
Det olinjära sambandet mellan in och utsignal ger upphov till udda distkomponenter. Asymetrin runt arbetspunkten ger upphov jämna distkomponenter.
Vad som också går att uttyda hoppas jag, trots att kurvan är asymetrisk, är att
olinjäriteten mellan in och utsignal får till följd att ju större insignalens sving är kring arbetspunkten desto mindre kommer förhållandet bli mellan in och utsignal, dvs det finns en amplitudberoende komprimering -starka signaler förstärks inte lika mycket som svaga. Starka musikpartier kommer alltså att "tystas" (eller så kan man se det som att svagare partier kommer fram bättre).
edit:förtydligande
Hevi, du skriver "olinjäritet mellan in och utsignal". Vad är insignal och vad är utsignal? Jo, insignalen är en spänningsförändring på gallret medans utsignalen är en olinjär strömförändring över anodmotståndet, men anodmotståndet är också olinjärt med anodströmmen.
Jag vill nog förtydliga kurvan. Om man definierar insignalen som en spänningsförändring på ingången d v s på gallret och utsignalen som
spänningsförändring på utgången d v s på anoden över en belastning så ges förstärkningsfaktorn av utspänning/inspänning. Det betyder att om man skall söka olinjäriteter så är det olinjäritet i förstärkningsfaktorn som är väsentlig.
Det är alltså inte olinjäriteten i brantheten som är den väsentliga parametern. Det man ser i kurvan är en spänningsförändring på ingång (galler) som ger upphov till en strömförändring på utgången (anoden). Detta kallas även för branthet eller transkonduktans.
Men eftersom anodresistansen också är olinjär med avseende på anodströmmen så måste man ta hänsyn till detta då man skall studera linjäritet på triodens utgång.
Jag försökte poängtera detta i mitt tidigare inlägg.
μ=Ri*gm. Denna ekvation gäller under vissa förutsättningar, nämligen att trioden är obelastad på anodsidan och jordad på katodsidan. Då får man fram det teoretiska maximala värdet på μ.
Om man synar linjäriteten hos anodresistansen så ser man att anodresistansen minskar med ökad anodström d v s anodresistansen bildar en kurva som funktion av anodströmmen genom röret och är aldrig en linje. Anodresistansen är alltså olinjär med anodströmmen genom röret d v s med utstyrning av röret.
Minskas anodresistansen med högre utstyrning d v s högre anodström så skulle även förstärkningsfaktorn μ minska enligt ovanstående formel under förutsättning att brantheten skulle vara konstant μ=Ri*gm d v s då skulle även μ vara lika olinjär som anodresistansens olinjäritet.
Men eftersom även brantheten gm ändras med anodströmmen och brantheten ökar med ökad anodström d v s då man styr ut röret,
så bibehålls förstärkningsfaktorn någorlunda konstant under förutsättning att den olinjära kurvan hos anodresistansen och den olinjära kurvan hos brantheten är lika olinjära med anodströmmen och att olinjäriteterna är varandras invers.
Då tar dessa båda olinjäriteter ut varandra och μ förblir konstant vilket betyder att utspänningen är linjär gentemot inspänningen. Är μ konstant blir distorsionen på utgången låg. Det är detta förhållande som råder i trioder då arbetspunkten väljs med omsorg och då man inte lastar trioden samt har jordad katod.
Jag tänkte lägga in lite kurvor på inre motstånd Ri, brantheten S och förstärkningsfaktorn μ. Allmänt ser man att högre anodström genom röret ger en arbetspunkt med linjärare μ. ECC83 ser minst rolig ut, men å andra sidan har den högst μ. Jag kan tänka mig att EF806 triodkopplad kan vara betydligt bättre då man vill ha högt μ.



ECC82 ser inte så pjåkig ut.

Här syns kurvornas olinjäriteter klart och tydligt. ECC88 och ECC82 ser bäst ut vad gäller konstant μ-faktor och har också lägst THD då man mäter.
MvH
Peter
VD Bremen Production AB + Ortho-Reality AB; Grundare av Ljudbutiken AB; Fd import av hifi; Konstruktör av LICENCE No1 D/A, Bremen No1 D/A, Forsell D/A, SMS FrameSound, Bremen 3D8 m.fl.







