JM skrev:petersteindl skrev:JM skrev:Går det inte att lokalisera ljudkällor i rum under välfiltrerade 80 Hz kan du inte uppfatta tidsskillnader i ljudet från olika subbasar. Problemet är att multipla tryckmin/tryckmax uppträder i fixa positioner i rummet. Med subbasarna i hörnen skapas interferenser vilka minskar olinjäriteter i tonkurvan skapade av stationära tryckmin./max..
JM
Jag tror inte att även om man inte kan lokalisera basmodulen så kommer den inte påverka slutresultatet. Mycket negationer i meningen.
Jag utgår från att även om man inte kan lokalisera basmodulen så påverkar den ändå slutresultatet, både i tidsdomän och i frekvensdomän. Hörseln Hanterar dessa två domäner på olika sätt. Tonhöjd exempelvis, hanteras även eller helt i tidsdomän enligt forskning som bedrivs idag. Det är detta med tidsdomän och stereofoni jag studerar för tillfället just nu. Det är synnerligen fascinerande.
Mvh
Peter
Över 80 Hz är tidsdomänen mycket viktig. Även om du inte kan lokalisera ljud i den psykologiska världen under 80 Hz påverkar subbasarna i tidsdomänen i den akustiska världen mha interferenserna i tryckmax/min och därmed skapas bättre hörbar tonkurva i frekvensdomänen?
Om jag har fattat rätt uppträder ett stationärt tryckgradientfält i rummet under 80 Hz vilket påverkas i tidsdimensionen olika beroende på var i rummet subbasarna är placerade. Eller lite annorlunda uttryckt - fasskillnaderna i ljudet från subbasarna skapar interferenser och därmed en rakare tonkurva enligt Welti.
JM
Detta som jag blåmarkerat bör nog analyseras djupare om man skall få någon rätsida på saken. Du skriver "stationärt tryckgradientfält". Inom vektoranalysen är en gradient per definition en differens d v s en derivata av en skalär funktion med fler variabler i det euklidiska rummet. Det är således en rumsderivata. En tryckgradient hos en ljudvåg är en vektor av ett tryck och vektorn visar riktningen på en utbredning av en ljudvåg i en viss riktning som ges av normalen mot fältets tangent.
Detta ser ganska olika ut för plana kontra sfäriska ljudtrycksvågor. Jag vet inte ens om en gradient som uttrycker derivata och riktning kan vara stationär, såsom du skriver? Jag får det till att derivatan snarast är noll d v s tryckgradienten är noll i en stående våg. I Weltis rapport finns varken ordet ”gradient” eller ”field” med. Han uttrycker sig inte med de orden.
Låt säga att bashögtalaren alstrar akustiska ljudvågor i form av sinustoner som varar en längre tid d v s flera perioder. Dessa vågor har ljudtryck och fortskrider i rummet genom luften. Då kan det se ut så här om man ser vektorer:
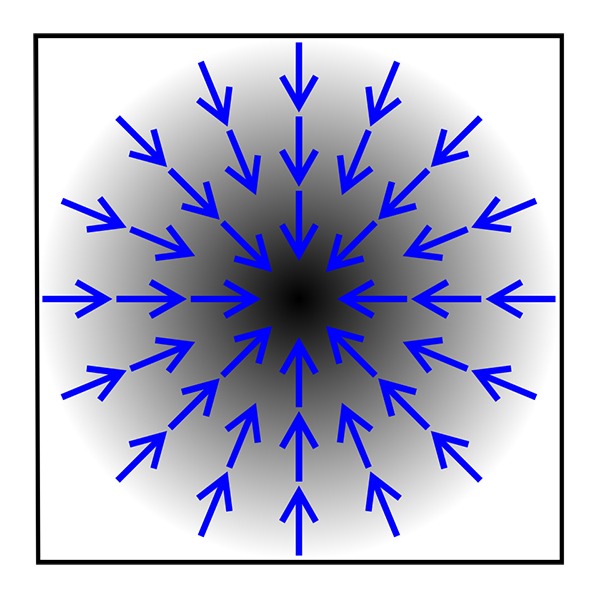
- Gradient spherical.jpg (186.34 KiB) Visad 3190 gånger
Man kommer snabbt in i vektoranalysen och då blir det komplicerat, men man bör åtminstone snudda vid vektorer om man skall använda begreppet gradient. Eftersom vågen är sfärisk så kan man rita upp vektorer i normalens riktning mot vektorfältets utbredning. Vektorfältet utbreder sig som en sfär från centrum på basen. Utbredningsriktningen är de blå linjerna. Själva fältet är vinkelrät mot dessa linjer och linjerna är normalen mot tangenten på fältet i varje punkt. Fältets utbredningen sker således i normalen mot fältet. Detta är själva ljudvågen med dess våghastighet som vi också kallar ljudets hastighet i luft.
I ett vektorfält är varje punkt i rummet tilldelat en vektor.
I ett skalärfält är varje punkt i rummet tilldelat en skalär. Ljudtryck i sig är en skalär storhet. Trycket i ett rum är ett skalärfält; för varje punkt i rummet finns ett tryck som anges med ett reellt tal.
Alstras en ljudvåg med givet ljudtryck där vågen propagerar/fortskrider i ett rum så kan ljudvågens tryck och riktning mätas i varje punkt, vilket kan representeras av en vektor som representerar fältets utbredning. Detta kan uttryckas som en gradient, en tryckgradient. tillförd energi fortskrider i vågen.
Gradienten = operator inom vektoranalysen: Gradient mäter hastighet och riktning av förändringar i ett skalärfält; Gradienten av ett skalärfält är ett vektorfält.
Då tryckgradienten/ljudvågen når en vägg med vinkelrät infallsvinkel mot väggen uppstår ett fenomen inom akustiken som kallas stående våg. Det är alltid så och oberoende av frekvens.
Vågen reflekteras mot ytan och byter riktning.
Är infallsvinkeln 90 grader mot väggen så reflekteras luftpartiklarna i ljudvågen vinkelrät mot väggen och vågen byter riktning genom att därefter fortskrida i motsatt riktning d v s vektorn hos den infallande ljudvågen mot väggen summeras med den reflekterade vågens vektor som ju går i motsatt riktning. Vektorsumman får värdet noll. Vågens partikelhastighet vid väggen är noll. Det betyder inte att trycket vid väggen blir noll, snarast tvärtom! Trycket vid väggen ökar till det dubbla d v s + 6 dB om väggen reflekterar 100 %. Men riktningen försvinner i och med att summan av vektorerna hos tryckgradienten blir noll. Man kan se det som 2 lika starka ljudvågor vars vektorer går i motsatt riktning mot varandra och i fas. Det där med fasen i tryckgradienten och reflexen är lite speciellt och åskådliggörs bäst med bilder och påverkas av position av ljudalstraren, men den diskussionen får bli vid annat tillfälle.
Vi förutsätter forcerad sinuston i resonemanget. Man tillför således energi med konstant amplitud till systemet. (Med impuls som input, så varar energitillförseln till systemet enbart under impulsens tidslängd. Impulsen kallas en fri våg och inte forcerad våg.)
Man kan se fenomenet stående våg ur en annan synvinkel:
Det intressanta är dels att den maximala amplituden blir dubbelt så stor som hos den infallande vågen, dels att tids- och lägesvariationen blir separata faktorer.
Intill väggen vid x = 0 har trycket ett maximum. Här är amplituden två gånger infallande vågens amplitud. Avlägsnar vi oss från väggen finner vi sedan periodiska maxima och minima.
I praktiken går minima inte helt ned till noll, eftersom reflexionen vid väggen inte blir fullständig.
På liknande sätt varierar partikelhastighetens amplitud med avståndet från väggen, men här är hastigheten noll vid väggytan. Envelopperna för tryck och hastighet i rummet är 90 grader förskjutna mot varandra.
Energidensitetens två komponenter, den kinetiska och den potentiella, fördelas i rummet.
Summan av dem är konstant i rummet och lika med summan av den infallande vågens och den reflekterades.
Hos en fortskridande våg är tryck och hastighet i fas. Här, i den stående vågen, ligger de nu fasförskjutna med π/2 = 90 grader. Detta innebär paradoxalt nog att intensiteten är noll.
Intensiteten är en rymdvektor som visar storlek och riktning på energitransporten i vågen. Infallande våg och reflekterad våg transporterar lika stor effekt per ytenhet, har samma intensitet, men i motsatta riktningar mot varandra. Detta är bakgrunden till att denna typ av våg kallas STÅENDE VÅG. En stående våg transporterar ingen energi. Att beakta är att med forcerad sinusoid våg så tillförs energi kontinuerligt till systemet. Vad händer med den energin?
Jo, en stående våg lagrar den energi som pendlar mellan kinetisk och potentiell, både i tiden och i rummet. Denna lagring av energi blir sedan till en bov vid resonans mellan väggarna.
Då denna våg når motsatt vägg i rummet så studsar den åter vinkelrät mot den väggen. Då kan man räkna ut att de frekvenser hos ljudet d v s periodiska multiplar av frekvensen och därmed periodiska inversen på våglängden som motsvarar avståndet mellan väggarna så kommer vågen färdas fram och tillbaka i fas. De kallas egenresonanser. Vid varje vägg uppstår tryckmax. Sammanfaller vågens partiella våglängder med avståndet mellan väggarna så uppstår resonans mellan väggarna och om energi tillförs under en längre tid än våglängden så lagras energin i resonansen och frigörs senare i tiden.
Man får så kallade trycknoder längs x-, y-, och z-axlarna i rummet. Tillsammans ger de en beteckning för en viss RESONANSMOD eller EGENMOD hos rummet. Moden (0,0,0) är trivial och motsvarar att man pumpar upp rummet till konstant tryck.
Ljudvågens hastighet kallas även utbredningshastighet, eller med alternativa benämningar, fashastighet, gånghastighet, våghastighet, ljudhastighet. Detta är den hastighet med vilken vågmönstret breder ut sig i mediet, luften.
Ett sak att beakta är att väggarna är parallella. Ljudkällan alstrar en sfärisk ljudvåg men resonansen mellan väggarna är i princip en plan ljudvåg eftersom vi räknat på vinkelrät infallsvinkel. Då ser vektorerna med dess vektorfält hos tryckgradienten snarast ut så här:

- Gradient plane.jpg (181.03 KiB) Visad 3190 gånger
Det är alltså väldigt olika vågor och vektorfält det handlar om. Direktljudet har sfärisk vågutbredning. Resonans mellan väggar är genom plan vågutbredning. Sedan får man ta hänsyn till avståndsregeln då man räknar på amplitud och man måste lägga in viss absorption vid simulering om inte resultaten skall bli helt tokiga.
I princip alla simuleringar som jag sett så utgår man från att vid rumsresonans har plana vågor uppstått. Det kan man enkelt se på det 3-dimensionella rutmönster som visas mellan tryckmax och tryckmin i rum.
En viktig parameter att ta hänsyn till är den väggreflex från högtalarväggen d v s bakom högtalarna som inverkar på direktljudet. Denna inverkan finns även med i den stående vågen från lyssnarens bakvägg d v s dess förstareflex samt vid resonans d v s fortsatta reflexer mellan lyssnarens fram och bakvägg.
Det blev tyvärr ett långt inlägg och jag hinner inte korrekturläsa. Lilltroll och jag har gjort åtskilliga simuleringar och animeringar på ljudvågsutbredning i rum som varar under en viss tid där man ser hur resonanser byggs upp och hur direktljudet förstörs och hur det korrupta direktljudet hela tiden reflekteras mellan väggarna och hur det skiljer sig på olika lyssnarplatser. Vi har även simulerat med impuls som input för att öka förståelsen vad som händer med icke-stationär signal. Varje animering är en väldigt stor fil, några hundra MB. Vad jag minns har lilltroll även simulerat med Navier – Stokes-ekvationer och det blir mer komplicerat.
Då jag och lilltroll har mer tid så är tanken att åtskilligt av vårt arbete kommer att läggas upp på tuben eller på min hemsida som jag tyvärr inte har tid att ägna mig åt för tillfället. Det får bli senare då serieproduktion av högtalarna förhoppningsvis kommer igång och leverans i större omfattning kan ske.
Mvh
Peter
VD Bremen Production AB + Ortho-Reality AB; Grundare av Ljudbutiken AB; Fd import av hifi; Konstruktör av LICENCE No1 D/A, Bremen No1 D/A, Forsell D/A, SMS FrameSound, Bremen 3D8 m.fl.
