Eftersom högtalarens impedans varierar med frekvensen så ger en icke försumbar kabelresistans en hörbar tonkurvepåverkan. Om högtalartillverkaren har konstruerat högtalaren med en försumbar kabelresistans i åtanke, så uppför sig inte högtalaren som konstruktören har tänkt sig.
Det blir också en viss förlusteffekt i kabeln om dess resistans inte är försumbar. Detta spelar dock mindre roll (i betydelsen att man förlorar effekt och därmed ljudstyrka). Det är just att förlusten drabbar olika frekvenser olika som är viktigt.
En kabel har både resistans, kapacitans, induktans, impedans och karaktäristisk impedans.
Resistansen är kopparns motstånd mot ström, typiskt ligger den väl under 1 ohm i en högtalarkabel. Den hamnar i serie med lasten, effektivt.
Kapacitansen kommer sig av att det är två ledare som ligger nära varandra och bildar en kondensator. Den hamnar parallellt med kabeln.
Induktansen kommer sig av att kabeln bildar ett enda varv på en spole. Det blir ju en slinga fram och tillbaka till högtalaren. I detta enda varv bildas ett magnetfält och därmed får man en liten induktans. Att tvinna kabeln minskar induktansen eftersom magnetfälten från kabelns intilliggande delar kommer att motverka varandra. Induktansen hamnar i serie med lasten.
Så här blir det:
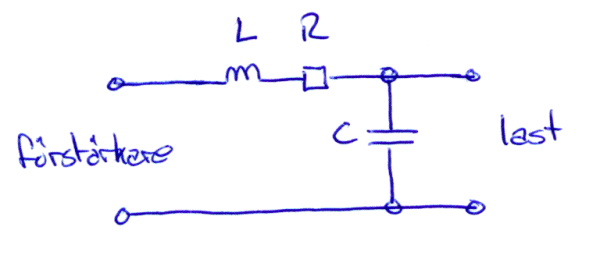
Alla tre egenskaperna ger kabelns impedans (vilket är skiljt från den karaktäristiska impedansen). Man kan se att kabeln uppträder som ett lågpassfilter. Nu funkar den här modellen bara för frekvenser väl under lågpassfiltrets brytfrekvens, men där funkar den bra. Audiofrekvenser är inget problem i sammanhanget.
Samtidigt kan man undra varför inte schemat ser ut så här:
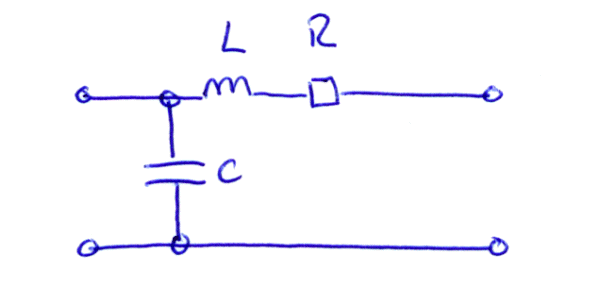
Svaret är att det gör det. Också. Tittar man nära på alla egenskaper
för låga frekvenser så är de samma för de två kretsarna. Kapacitansen är ju egentligen distribuerad över hela kabelns längd, och vill man vara lite noggrannare så kan man rita kretsen på någon av de här sätten:
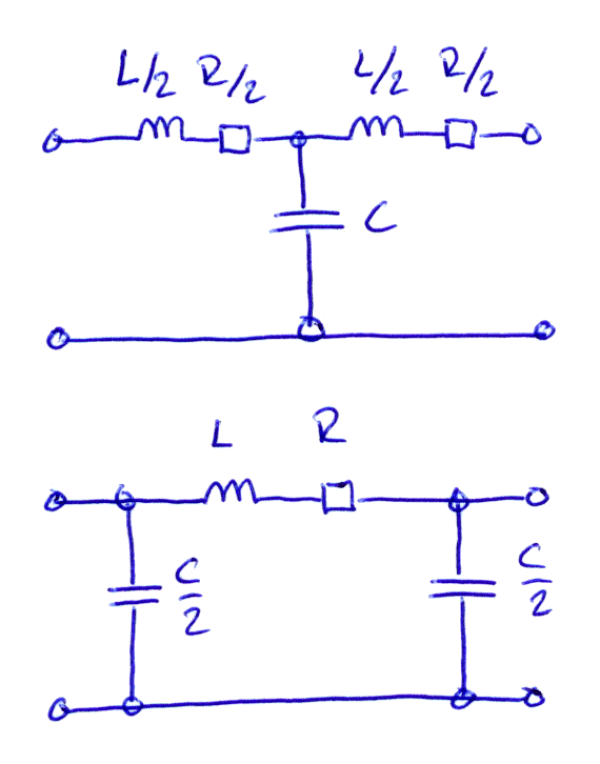
Eller om man går ytterligare ett steg så kan man dela upp kabeln i små snuttar, så här:
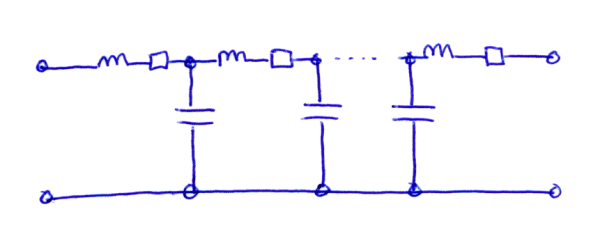
...då kan man få en modell som funkar även för höga frekvenser. Eftersom kretsen nu innehåller många spolar och kondensatorer så kan man förstå att det kan bli många resonanser i kretsen. De resonanserna är de stående vågor som kan uppstå vid riktigt höga frekvenser.
Men karaktäristisk impedans då, vad är det? Jo det är en resistans...

Den resistansen/impedansen är något helt annat än kopparns resistans. Jag har en alldeles egen intuitiv förklaring på hur den uppkommer: Om man tänker sig att man plötsligt slår på spänningen i förstärkaränden, så kommer en våg att breda ut sig i kabeln. Vågen har en utbredningshastighet och precis i början vet ingen att det sitter en högtalare i andra änden av kabeln. Det enda som märks är strömmen som går åt för att ladda upp kabelns kapacitans, och då den del som sitter närmast förstärkaren. Eftersom vågen utbreder sig med konstant hastighet så går det åt en viss mängd laddning per tidsenhet för att ladda upp de nytillkomna kapacitanserna till spänningen som vi lade på kabeländen. Laddning per tidsenhet, det är ström det. Så länge som vågen inte har nått kabeländen kommer det alltså att gå en konstant ström in i kabeln. Konstant spänning, konstant ström. Hmm, det blir ju en resistans! Detta är kabelns karaktätistiska impedans.
Om kabeländen är öppen så kommer vågen att studsa tillbaka och lika lång tid senare märker man det i förstärkaränden som en impedansändring. Illa dimensionerade förstärkare kan råka i självsvängning av detta. Om man däremot
avslutar kabeln med en resistans, dvs kopplar ett motstånd i högtalarens ställe, som har samma resistans som kabelns karaktäristiska impedans, då blir det ingen reflexion. Motståndet tar vid och absorberar ström precis som kabeln gjorde på vägen.
Hmm, undrar om jag svarade på ursprungsfrågan...

Så länge har jag längat efter att loudness war skulle vara över. Nu börjar jag tro att vi faktiskt är där. Kruxet är att vi förlorade.




