Svante skrev:Utimpedans 200 ohm. Uppskattad kabelkapacitans 10x200pF.
Brytfrekvens f0: 1/(2*pi*200*2000e-12)=400 kHz
Dämpning vid 20 kHz: 20*log(1+(20/400)²)=0.02 dB
Inte så illa som förklaring med tanke på att kabelkapacitansen gissades till 200 pF/m.
EDIT: MERPARTEN AV ANTAGANDENA NEDAN ÄR FELAKTIGA. KLARHET KOMMER FÖRHOPPNINGSVIS FRAMÖVER!

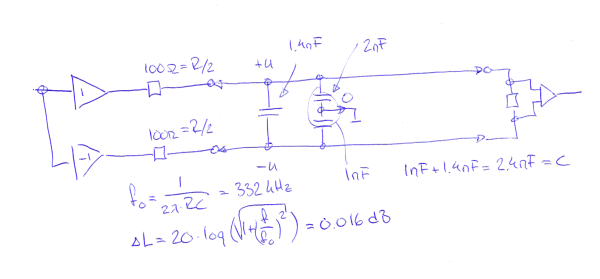
Inte illa alls med tanke på att jag mätte upp kapacitancen till 1.4nF dvs 140pF/m mellan ledare/ledare.
MEN sedan har vi ju också kapacitancen ledare/skärm på 2nF = 200pF/m men jag har svårt att greppa hur det påverkar. Lär väl bero på typ av utgånssteg...

I det här fallet är det ett impedansbalanserat steg.
Om jag tänker rätt så bör impedansbalanseringen innebära att den totala kapacitance blir ledare/ledare + ledare/skärm = 340pF/m.
Ovanstående indikerar en högre avrullning än vad både Svantes beräkning ger och mätningen. MEN mätningar är ju inte perfekta (eller kanske man ska säga att piloten inte är perfekt..) och jag körde en mätning i dag med samma uppsättning fast med svep och stegad sinus i stället för brus och jag fick då en något högre avrullning som förmodligen synkar bättre med uppmätt kapacitans.
Hahahaa nu börjar det klarna, det hela blir ju lite komplext att räkna på. Impedansbalanseringen innebär ju att signalen (pin 2) ser dels kapacitansen via skärmen till jord (via R1 = 100ohm förmodat) men sen även kapacitansen ledare/ledare där signalen går via det impedansbalanserande motståndet R2 = 100ohm till jord.
Om vi ser kapacitansen som kortslutning vid väldigt höga frekvenser så resulterar de två motstånden i den impedansbalanserande kopplingen ett nettomotstånd på R1xR2/R1+R2=50ohm.
Ett alternativt och möjligtvis något klarare och mer korrekt sätt att se det hela på kan ju vara följande:
Utgångsstegets belastning vid höga frekvenser består utav två RC länkar till jord, R1 och C1 (100ohm 2nF) samt R1+R2 och C2 (200ohm
1.4nF).
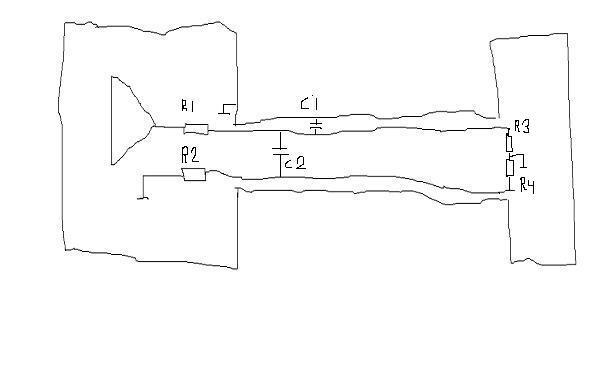
Så god natt! Nu har jag tänkt klart för i dag.
p.s. ritade med fingret på pekplattan i paint därav den konstnärliga touchen på schemat ovan!

/Peter