Naqref™ skrev:Skulle vilja hålla med varenda ord IÖ skriver om efterklangstid. Det sagt så skulle jag inte därmed vilja säga att Matts har entydigt fel.

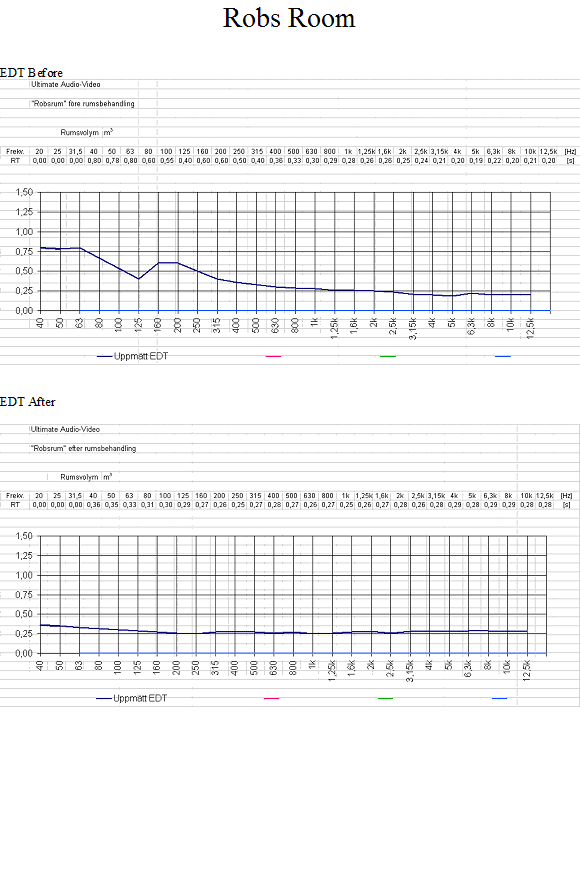
I bilderna IÖ refererar till så ser man tydligt att de utgår ifrån en statisk excitation av rummet och då stämmer resonemanget oftast ypperligt. Men Matts mäter med (om jag tolkar graferna rätt) med impulsljud. Då kan man inte använda betydelsen T(20)=RT60/3. Man kommer nämligen ha minst tre olika områden med potentiellt olika derivata och det är först den sista delen som motsvarar den klassiska RT60.
Den första delen beror på "di tidiga reflexerna" d v s de primära reflexerna i närheten av ljudkällan och mikrofonen. Här kommer placering av högtalare och mikrofon vara avgörande samt lokala diffuseringar och dämpningar av dessa diskreta reflexer att spela stor roll för derivatan. Den andra delen beror delvis på det förstnämnda men gissningsvis mer på storleken på rummet. Det är området där man har 3 studsar eller något mer. Först när man kommer upp i rejält många studsar så närmar vi oss den traditionella RT60. Tyvärr kan nivån ha blivit för låg om man mäter med impulsljud för att man ska kunna få ett rättvist värde på detta. Vid vilka tidsintervall man ligger för respektive område beror på medelgångvägstiden mellan reflexer för rummet.
Hej, jag känner att vi inte är klara med den här bra tråden, för många har efterlyst förtydliganden på påståenden från Matts m fl. För dessa rekommenderar jag att ni sätter er in i begreppen smårumsakustik och begreppet diffusion, maskering mm. Matts har enligt mig redan förklarat vad som utmärker ett Level 3 rum, 7e inlägget från botten på sidan 8 i tråden. Vidare förklarar han också sin syn på varför han förespråkar diffusion istället för mjuka absorbenter. Det finns en fundamental skillnad mellan diffusorer och mjuka diffusorer, det är att i en mjuk absorbent blir ljudenergin värme (dvs den försvinner), med diffusion sänks reflexens nivå på motsvarande sätt MEN ljudenergin finns fortfarande kvar i rummet, som en dämpad men diffus bredbandig efterklang. Finessen är att designa sitt rum med diffusorer så att denna diffusa klang hamnar på en behaglig och optimal nivå.
Anmärkning på ovanstående citat 1:
Om du mäter med impulsljud blir det väl samma resultat som med avbrutet statiskt brus i smårum? Förutsatt att du inte använder en impuls utan tillräcklig dynamik (SNR).
Varför påstår jag detta? jo för att den där grejen med att vänta tills nivån fallit de första 5 dB enligt tidigare bild gör resultatet "ganska" lika, för på den tid 5 dB tar på sig har rummet redan erhållit ett reflektionsfält tillräckligt "likt" ett som du har med avbrutet statiskt brus efter 5 dB decay.
Du befinner dig alltså redan då i "området där man har 3 studsar eller något mer".
I ett kontrollrum med uppmätt RT60 0,3 sekunder kan vi approximativt anta att de första 5 dB decay vi har från direktljudsnivå har ljudet färdats ca 8 m ytterligare och studsat lite här och var i smårummet innan det når mätmikrofonen.
Anmärkning på ovanstående citat 2:
Rimligen kan vi ALDRIG anta T(20)=RT60/3 oavsett mätmetod, förutsatt att vi följer nomenklatur enligt IÖ i tidigare inlägg, eftersom då T(20) = RT60. Då T(20) approximerar RT60 genom utvärdering från -5 - -25 dB i decayförloppet.
Tänk vad skillnad mellan med/utan suffix på T20 kan ställa till det

...och så lite generell fakta om Sabines formel:'
Formel kan användas för att BERÄKNA efterklangstid i rum under förutsättning att vissa villkor uppfylls i rummet. (Ett flertal medlemmar på denna sida verkar tro att Sabines formel har något med definition på det vidare begreppet efterklangstid att göra, vilket den inte har)
- Rummet förutsätts ha ett diffust ljudfält
- Medelabsorptionsmängd i rummet skall vara större än 0,3 m2S(abine)
Det är alltså en formel som bygger på att statistiskt har ett rum med en viss volym och en viss absorptionsmängd en efterklang enligt formeln. FÖRUTSATT ovan givna kriterier.
Sabines formel gäller ej heller i större lokaler eftersom den ej tar hänsyn till luftdämpningen, en dominerande efterklangssänkande faktor i t ex Göteborgs konserthus. Där är den snarlika Eyrings formel bättre att använda vid snabb estimering.
Eftersom Matts (SMT) tidigare efterlyste en diffusionkoefficient i Sabines formel kändes det nödvändigt att dra "the basics" om denna formel. Full diffusivitet är liksom redan inbyggd. Möjligen menade kanske Matts en komplettering av formeln för rum med odiffust ljudfält? Då blir det att ta till finare beräkningsmetoder som FEM och strålgångsprogram.
Till de som undrar hur mätinstrumenten mäter så utvärderar de RT60, ibland under beteckningen T(20) och ibland T(30).
(xx) betyder suffix

Begreppet efterklang för ett ljudfält i rum definieras som IÖ tidigare visat på bild från den tid det tar för ljudnivån att dämpas 60 dB.