IngOehman skrev:Nä.
Fasmodulation är kanske ett bättre ord för förvrängningen som uppstår då ett element ska spela låga och höga frekvenser samtidigt?
Moderator: Redaktörer
IngOehman skrev:Nä.
Svante skrev:Åkejrå, jag kanske får ge mig där.
Svante skrev:Men hursomhelst så är det lite skillnad på detta och det vanliga "liten i förhållande till våglängden", eftersom det är det lilla som blir kvar efter skillnadssignalsbildningen som är viktigt. 3,44 meter och 3,44 cm isär ger fortfarande 1/100 kvar vilket är 40 dB ner.
Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
dawen skrev:Används det här elementet i någon Inokonstruktion man känner till? Det låter onekligen som ett intressant element.
De spektrala komponenternas utbredning i tidsdomän är nämligen större än pulsens bredd, redan från början, det är bara det att det inte syns när pulsen ser kort ut.
IngOehman skrev:Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Det har jag inte gjort. Jag spekulerar bara. Nollhypotesen är en bra utgångspunkt dock, i många vetenskapliga frågeställningssammanhang, tycker du inte?
Ingen av oss lär kunna bevisa att det inte går att höra vågningen off axis, men kanske någon av oss kan visa att det går? Exempelvis den som tror att det går...
IngOehman skrev:Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Nu blir jag stum igen. För ett ögonblick.

Nu, när stumheten gått över frågar jag mig (och dig) denna humanistiska (krusfria) fråga:
Hur kan ett system som påstås vara linjärt och ringande, släppa igenom en signal utan att påverka den, trots att signalen ifråga har en bandbredd lika stor som systemts bandbredd?
Rätt svar: Det kan det inte! Således: Systemet ringer tydligen inte.
IngOehman skrev:Sen är jag den förste att erkänna att den vetenskapliga världen (av idag) bryr sig inte om att distingera mellan orsakerna till vågning, utan kallar allt ringning. Jag gör det inte dock, och kommer inte börja göra det idag heller.
[/size]
IngOehman skrev:Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
Spekulation: Då tror jag att det var ett försök med bara ett LP- eller ett HP-filter, och inte summan av de två?
IngOehman skrev:
Alla branta filter låter nämligen som om de ringer när de inte sällskapas av sin andra hälft.
IngOehman skrev:Det beror på att de har ett "vasst knä" sedda ensamma. Knäets frekvens tillåts dominera över sina kringliggande frekvenser.
Piotr skrev:IÖ skrev;De spektrala komponenternas utbredning i tidsdomän är nämligen större än pulsens bredd, redan från början, det är bara det att det inte syns när pulsen ser kort ut.
Tror jag nosat på det här förut, skall se om jag hänger med.
En puls innehåller "samtliga" frekvenser pga, oändlig bandbredd men dock under en kort begränsad tid.
Impulsen kan inte se ut som den gör utan högfekvens innehåll, utan skulle då se annorlunda ut och viktigast av allt, den mer lågfrekventa energin i pulsen har i själva verket startat tidigare än vad det ser ut som med HF innehållet?
Tror jag kanske förstår men vet inte om jag förklarar mig vidare bra..
/Peter
Svante skrev:IngOehman skrev:Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Det har jag inte gjort. Jag spekulerar bara. Nollhypotesen är en bra utgångspunkt dock, i många vetenskapliga frågeställningssammanhang, tycker du inte?
Ingen av oss lär kunna bevisa att det inte går att höra vågningen off axis, men kanske någon av oss kan visa att det går? Exempelvis den som tror att det går...
Ja, det är ju det jag brukar säga till de som hör saker som inte jag tror på. Man kan ju tänka sig en simulering här faktiskt, att man tar en hög- och en lågpassgren och fördröjer den ena i datorn och ser om det hörs någon ringning. Fast, förstås blir det svårt att skilja från en eventuell tonkurveavvikelse, eller så är det bara ett dumt försök att skilja två begrepp från varandra (tonkurva/ringning) mha ett lyssningstest, det kanske inte går. Hmm.
Svante skrev:IngOehman skrev:Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Nu blir jag stum igen. För ett ögonblick.

Nu, när stumheten gått över frågar jag mig (och dig) denna humanistiska (krusfria) fråga:
Hur kan ett system som påstås vara linjärt och ringande, släppa igenom en signal utan att påverka den, trots att signalen ifråga har en bandbredd lika stor som systemts bandbredd?
Rätt svar: Det kan det inte! Således: Systemet ringer tydligen inte.
Jomen... Förklaringen ligger ju hoppandet mellan tids- och frekvensdomän... Ringning definieras i min värld i tidsdomänen. Det är ett utklingningsförlopp i tidsled. Tittar vi på tidssignalen så har den in- och utringning (urringning?).
Svante skrev:Om vi i stället väljer att titta i frekvensdomänen så kan vi inte tala om in- och utringning, eftersom ringning är ett begrepp som förklarar hur signalen beter sig i tidsled.
Svante skrev:Jag kan kontra med ett motexempel, tag det där 2:a ordningens lågpassfiltret med Q=10 och f0=1000 Hz. Kör in en sinc, bandbegränsad till 10 Hz. Ringer det nu? Knappast, signalen ser i det närmaste identisk ut med det vi stoppade in.
Svante skrev:Kan man av detta dra slutsatsen att ett sådant filter inte ringer?
Svante skrev:(nej insignalen har inte samma bandbredd som systemet, men varför ska vi ha just den begränsningen, som är i frekvensdomänen, när vi undersöker tidsförlopp).
Svante skrev:IngOehman skrev:Sen är jag den förste att erkänna, att den vetenskapliga världen (av idag) bryr sig inte om att distingera mellan orsakerna till vågning, utan kallar allt ringning. Jag gör det inte dock, och kommer inte börja göra det idag heller!
[/size]
Nja, det är ju en lite tråkig inställning, att inte vara beredd att ompröva sin tro. Det är tur att det står "idag" där, vi får väl hoppas på "i morgon", då.
Svante skrev:iö skrev:Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
Spekulation: Då tror jag att det var ett försök med bara ett LP- eller ett HP-filter, och inte summan av de två?
Nix! Det var ett delningsfilter, dvs med både bas- och diskantkanal. Det var inklusive högtalarelement och rum, och det är klart att man kan kritisera elementen och säga att de inte var tillräckligt bra, och att ringningen hördes därför. Å andra sidan är det ju meningen att man ska kunna använda delningsfilter till just högtalare.
Svante skrev:IngOehman skrev:Alla branta filter låter nämligen som om de ringer när de inte sällskapas av sin andra hälft.
Jajustdet, och om inte elementen eller de rumsliga egenskaperna tillåter utsläckning av ringningarna, så kommer det att bli en rest kvar som i princip kan höras.
Svante skrev:Vad jag menar är att det är ganska noga med detta, dels får inte elementen sitta långt ifrån varandra och då talar vi om 1/10 våglängd eller nåt, dels får inte elementens tonkurva avvika från det planerade med mer än 0,8 dB om 1/10 ska vara uppfyllt.
Svante skrev:IngOehman skrev:Det beror på att de har ett "vasst knä" sedda ensamma. Knäets frekvens tillåts dominera över sina kringliggande frekvenser.
Ja, det där är ju ett synsätt.
Svante skrev:Ett annat skulle vara att örat faktiskt analyserar tidssnuttar av signalen, ungefär som ett spektrogram. En sån där omatematisk processning påhittat av en pragmatisk evolution. Om impulssvaret blir för utbrett i tiden, så spiller ringningen över i ett perceptuellt särskiljt tidsintervall, och då hör vi en ton.
Svante skrev:Det kan illustreras genom att ta sig en sinc (som den jag länkade till tidigare i tråden) och göra en FFT på en snutt före själva toppen. Eftersom örat gör något som liknar detta är det inte konstigt att vi hör en frekvens (ringningens, som "råkar" sammanfalla med knäet).
Vilket synsätt som är "rätt" kan vi nog diskutera i evighet.
IngOehman skrev:...
IngOehman skrev:För mig är ringning den fördröjda energiavlämning
som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats.
Morello skrev:Nu tror jag IÖ våldförde sig på definitionen av periodisk eller också var det bara ett stavfel.
Svante skrev:IngOehman skrev:För mig är ringning den fördröjda energiavlämning
som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats.
OK då, om vi nu tar en impuls, när avlämnar den sin energi? Jo vid ögonblicket för impulsen. Så får den passera genom ett brickwallfilter (som iofs är icke-kausalt, men strunta i det nu).
När avger sincen som kommer ur det sin energi? Jo efter och före (ochpå) tidpunkten för impulsen. Ett brickwallfilter har alltså både för- och efterringning.
Svante skrev:Visst, om vi exciterar filtret med en signal som inte framkallar ytterligare ringning, som en sinc, så ser vi inte ringningarna från filtret. Det gör vi inte heller i fallet med lågpasslänken (Q=10 f0=1000, exciterad av 10Hz-sinc) Men om vi exciterar filtret med en signal med frekvenser över f0 för brickwallfiltret, så syns de.
IngOehman skrev:Morello skrev:Nu tror jag IÖ våldförde sig på definitionen av periodisk eller också var det bara ett stavfel.


Förklara dig.
Vh, Ing. Öhman
IngOehman skrev:
Ser man på förloppet I TIDSDOMÄN, men sönderdelat i frekvensavsnitt, så ser man emellertid att respektive frekvensband inom hela CD-registret är HELT OSKADAT i tidsdomän.
IngOehman skrev:
Nä, typ alla signaler som håller sig under 22 050 Hz. Då syns bara (i förekommande fall) vågningar från den högsta (men fortfarande icke-tidsfördröjda) signalkomponenten. Det betyder att: CD-SYSTEMET SAKNAR RINGNINGAR INOM FREKVENSOMRÅDET 0 - 22 050 Hz!

Och det är trevligt!
Det skall vi vara glada över, och kanske till och med hoppa och skutta runt lite glatt (tjoa är också ok) om vi känner att vi måste. Det tycker jag är rimligt.
Tjohopp!
Vh, Ing. Öhman
markih skrev:Jag tycker rent intuitivt att IÖ har rätt i det att betydelsen av ordet ringning är kausalt
Om jag har läst rätt, jag har bara skummat väldigt snabbt, för ordväxlingen är verkligen utförlig

Dvs för-ringning är ett begrepp utan intuitiv och praktisk (i verkligheten fysikalisk) förankring. För-ringning kanske passar som ett matematiskt begrepp?
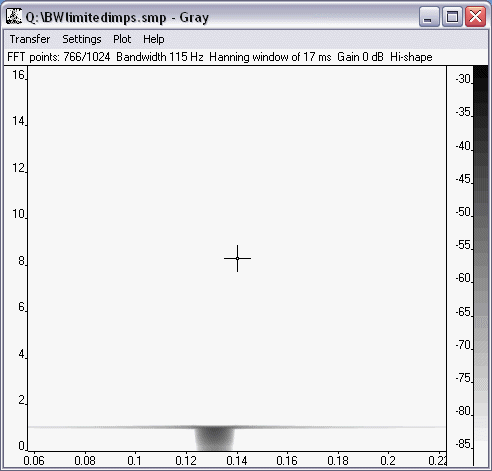
dimitri skrev:Svante,
Du visar en signal på 115 HZ och ett tidsfönster på 17 ms.

IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Användare som besöker denna kategori: zorro och 26 gäster