Moderator: Redaktörer
Hotspur skrev:Trevlig är hon också
OT: Du menar snygg?

lazyworm skrev:IngOehman skrev:DTS finns f ö i både 16- och 18-bitsversion..
Jag har fått uppfattningen att man kan spela in DTS i 24 bitar nu för tiden?
lazyworm skrev:IngOehman skrev:DTS finns f ö i både 16- och 18-bitsversion..
Jag har fått uppfattningen att man kan spela in DTS i 24 bitar nu för tiden?
Audiomanikern skrev:Hej!
Stenålder - det bör vara 64 bit / 3.53 MHz... minst juh!
Mvh A*
Harryup skrev:Fràgan kan ju bara leda till gissningar dà väl fà hört alla alternativen optimalt avspelade.
Om man fàr tro pà att Meridian har koll pà DVD-Audio sà skulle jag ranka en bra skivspelare (LP-12, Forsell) som likvärdig till DVD-Audio beroende pà program material, dom alternativ jag har hört när det gäller SACD, (hyfsat mànga) sà räcker inte kvalitén till för att matcha ens CD spàret pà samma skiva avspelad pà Meridian 800 mot Pioneer 868.
Piotr skrev:Harryup skrev:Fràgan kan ju bara leda till gissningar dà väl fà hört alla alternativen optimalt avspelade.
Om man fàr tro pà att Meridian har koll pà DVD-Audio sà skulle jag ranka en bra skivspelare (LP-12, Forsell) som likvärdig till DVD-Audio beroende pà program material, dom alternativ jag har hört när det gäller SACD, (hyfsat mànga) sà räcker inte kvalitén till för att matcha ens CD spàret pà samma skiva avspelad pà Meridian 800 mot Pioneer 868.
Vinyl likvärdigt DVD-A..? Skulle inte tro det. Om SACD spåret låter sämre än CD spåret på dina grejor så kan ett tips vara, byt skivor eller byt spelare. Jag har ett gäng SACD hybrid och det är ingen tvekan om att SACD är bättre än CD på tex. Opus3./Peter
Piotr skrev:Jag mistänker att de flesta anti SACDare jämfört som du beskriver och det säger en hel del (inte första gången jag hör talas om det..).
Piotr skrev:Håller med. Dock har de som lyssnat på mastertape vs. vinyl och SACD konstaterat att SACD är mycket närmare originalet än vinyl, speciellt den vinylkopian som når kund.
Låta bra och låta korrekt behöver ju inte alltid vara samma sak.. själv är jag dock en så´n där tråkig korrekt typ som vill ha sanningen, hela sannngen och inget anat än sanningen..
Tror nämligen att enda vägen till nya fantastiska upplevelser med en musikanläggning är via lägre färgning och signalpåverkan. Annars målar man in sig själv i ett hörn så att säga.
Är anläggningen totalt transparent så kan den fås att göra "vad som helst".. den skulle kunna låta som rör eller vinyl om detta kodats in i skivan. Man kan dock aldrig få ett transparent ljud från en färgad anläggning genom att mixa och mastra på hitan eller ditan väg.
I slutändan kommer ju alltid val och kompromisser in i verkligheten igen men ovanstående är min grundläggande inställning till välljud.
/Peter
Piotr skrev:Öhman,
det intressantär ju att den PCM infon som fås från nerconvertering av DSD ger ett CD spår som klår äldre PCM versioner av samma mastermaterial..
Kan ju (som jag beskriver ovan) bero på nya och bättre apparater för A/D processen, och en rykande färsk 16/44.1 direkt PCM kodning kanske skulle klå SBM spåret på en hybrid SACD, men än så länge har jag inte upplevt det.
Med andra ord, testet du rekommenderar har utförts och mitt intryck kvarstår och åsikt likaså, SACD äter CD.
/Peter
Margaux skrev:Tveksamt om jag skulle kunna höra skillnaden mellan CD, DVD-A och SACD i blindtest, nivåmatchat, samma källa, SOTA avspelare inom respektive kategori. Det är nästan lite kabeldiskussion över det hela. Mycket tycka och tro - lite verifierat via kontrollerat blindtestPlacebovarning här!
CD är tillräckligt bra. Det är mastringen och inspelningen som sätter gränsen i 99% av fallen.
PS. Jag tror endast detta då jag varken kan avspela DVD-A eller SACD hemma hos mig.
Margaux skrev:Tveksamt om jag skulle kunna höra skillnaden mellan CD, DVD-A och SACD i blindtest, nivåmatchat, samma källa, SOTA avspelare inom respektive kategori. Det är nästan lite kabeldiskussion över det hela. Mycket tycka och tro - lite verifierat via kontrollerat blindtestPlacebovarning här!
CD är tillräckligt bra. Det är mastringen och inspelningen som sätter gränsen i 99% av fallen.
PS. Jag tror endast detta då jag varken kan avspela DVD-A eller SACD hemma hos mig.
Helt utan överraskning så är det främst i toppoktaverna som skillnaden ligger, men även när det gäller upplösning och ljudbilden överlag som blir mer verklig och andas mer. Det känns klarare, öppnare men samtidigt en aning mer avslappnat.
Nu tror jag att de du hör Piotr inte är inbillning. Det skulle dock vara intressant att veta lite mer om mastern som ligger till grund för DVD-Aha upplevelsen. Har den verkligen så mycket information som 192kHz? Eller är det något annat som gör att det låter bättre, mastring till exempel? (jämför vinyl vs cd debatten)?
Hur förklaras rent vetenskapligt att DVD-A skulle vara bättre än CD?När jag kollade hörseln så hörde jag bara upp till 16 kHz. Men även om jag skulle höra upp till 20 kHz så var finns det vetenskapliga argumentet? Fler bitar? CD är totalt brusfritt i mina öron.
Därmed inte sagt att om man bygger en CD spelare utan jitter, perfekt vikningsfiltrering m.m. inte kan låta lika bra. Eller?
Piotr skrev:En annan sak som förvånar mig är det evinnerliga tjatet om att vi bara hör 20kHz. Detta handlar om sinustoner och man kan inte utan vidare anta att mer komplexa signaler inte skulle kunna ge ett helt annat resultat. Det finns ju fakstiskt numer ett antal studier (vissa tio år gamla eller mer) som verkar bevisa att vi detekterar ultraljud.
Däremot kan kanske ljud högre upp i frekvensregistet påverka ljud i det hörbara, på något sätt. Men jag tycker läget är oklart. Det räcker inte med att verka bevisa något. Det måste fram faktiska bevis, i repeterbara försök.
As part of the building of superconducting magnets, we have to use something called superinsulation, in 50 to 200 layers. They are made of alternating layers of aluminized mylar, for IR reflection...and a gauze like paper layer, to break conduction. The stuff is used in a vacuum, which removes convection.
Part of the process requires using ultrasonic transducers, piezo transducers with impedance matching feedhorns to the work tip. When the welder is activated, plastic touching the tip absorbs the energy, and melts..hence, plastic welding.
When this device is turned on, the background noise level within the production bay goes down. The ear is responding to the energy by reducing it's gain..it is a trivial thing to pay attention to the background noise, and detect the ultrasonic, not by the sound itself, but by the effect it seems to have on everything else that can be heard.
So, your statement "part of a normal signal is interesting, as I do indeed use the normal signal to detect the presence of the U/S.
norman skrev:Piotr: Tänkte likadant som dig om samplehastighet m.m. men det är fel (har nu läst lite signalteori). Efter det branta filter man har efter dac:en så kommer varje sample med värdet a att motsvaras av en a*sin(x)/x kurva, summerar du ihop dessa kurvor för alla samples så ser du att det kommer funka finfint úpp till halva samplehastigheten (men man har ju inte oändligt branta filter så det skärs av en bit innan)
alltså: Man kan exakt återskapa vilken vågform som helst upp till fs/2 (eller lite under med realistiska filter)
(är trött å seg så förklaringen är inte den bästa... men man kan ju hoppas att det kommer nån som är bättre på att förklara)
Om du jämför impulssvaret mellan CD och DVD-A och SACD så har du en stor del av svaret på varför de nya formaten låter bättre än det gamla. Musik är amplitud och tid, för att vara transparent måste formatet kunna följa båda axlarna utan nämnvärd påverkan av ursprungssingalen.
SACD har brus men kan följa den aktuella signalen vilket inte CD kan. CD är god upp till 5k eller så sen blir det problem.
Ledsen men tror inte 44.1k samplingsfrekvens kan inte fånga allt under 20k korrekt. Det är omöjligt. Topp oktaverna man hör på CD är kraftig distortion och vissa har svårt att vänja sig av med den.
För att med säkerhet kunna sampla en ren sinus vid 20k perfekt så krävs långt över två samples för varje period.
Låt oss säga att vi spelar in en ren 20k sinus med en mic och samplar med 40k. Vad händer om vår klocka råkar pricka av då kurvan råkar skära noll? Tystnad är resultatet. Sinusen på en cykel skär genom noll två gånger för varje period med exakthet och klockan samplar vid samma punkt varje gång.
Jag har känt till detta lite luddigt länge och hört utbildade personer uttrycka sig på båda sätt. Dvs. har hört folk "styrka" båda teorierna.
/Peter
Morello skrev:Norman, som är överdängare på matematik, kan säkert dra hela beviset av samplingsteoremet på nolltid
Rydberg skrev:Morello> Samplingsteoremet gäller inte heller trunkerade signaler
Harry Nyqvist bevisade redan på 1920-talet att det går utmärkt att sampla en signal, vars högsta frekvens är mindre än halva samplingsfrekvensen. Gör man detta kan signalen sedan återskapas helt utan förlust eller distorsion. Observera att teoremet inte säger något om själva kvantiseringen.
Någon kraftigt distorsion i toppoktaven excisterar inte inte en hyfsat korrekt implementerad CD-spelare. Vi talar om en typisk dist om cirka 0.001%.
[/quote]Piotr skrev:God kväll Morello!Harry Nyqvist bevisade redan på 1920-talet att det går utmärkt att sampla en signal, vars högsta frekvens är mindre än halva samplingsfrekvensen. Gör man detta kan signalen sedan återskapas helt utan förlust eller distorsion. Observera att teoremet inte säger något om själva kvantiseringen.
Ok, mitt exempel var inge vidare. MEN ovanstående gäller statiska signaler, det kan ju omöjligt gälla kaotiska signaler?
Harry tänkte på repetetiva signaler och inte transienter tror jag. Vilken knäppgök, transienter e skitkul ju.Någon kraftigt distorsion i toppoktaven excisterar inte inte en hyfsat korrekt implementerad CD-spelare. Vi talar om en typisk dist om cirka 0.001%.
Skulle va intressant att se följande;
Nå´n som har möjlighet att köra ett sån´t test?
/Peter
en enda period av en... 700Hz sinus ton överlagrad med en enda period av 20000Hz med start vid samma tid går in igenom A/D samt D/A och göra en analys på signal in och ut.
Rydberg skrev:Morello> Samplingsteoremet gäller inte heller trunkerade signaler
pinnick_swe skrev:jaghar läst sånt där ..en del men jag körde ju visserligen alla tentor för att jag bytte inriktning till något annatMen med färre samples så kan man missa en massa mikrodetaljer och förändringar i amplitud i tiden. Väldigt små men i alla fall? dessutom torde ju det försvinna en hel del som generaliseras bort när man återskapar signalen igen. Det är FFT man använder väl?
Kanske ska fixa tentorna innan jag skriver något mer
Svante skrev:Rydberg skrev:Morello> Samplingsteoremet gäller inte heller trunkerade signaler
Mja, samplingsteoremet gäller alla bandbegränsade signaler. Trunkerade signaler kan inte vara bandbegränsade i matematikens värld. Men om man lyckas med att dämpa allt över halva samplingsfrekvensen med säg 100 dB, så kan man återskapa signalen såpass noga att felet ligger 100 dB under fullskala.
.
Morello skrev:Svante skrev:Rydberg skrev:Morello> Samplingsteoremet gäller inte heller trunkerade signaler
Mja, samplingsteoremet gäller alla bandbegränsade signaler. Trunkerade signaler kan inte vara bandbegränsade i matematikens värld. Men om man lyckas med att dämpa allt över halva samplingsfrekvensen med säg 100 dB, så kan man återskapa signalen såpass noga att felet ligger 100 dB under fullskala.
.
Ja, men samplingsteoremet inkluderar detta helt nödvändiga villkor ang. bandbegränsing och således gäller det alltid, eller hur?
dawen skrev:Bill50x: Varför ska man ha verkligheten som referens?
dawen skrev:Nackdelen med verkligheten som referens är ju att den är omöjlig att återskapa. Givetvis kan du be en musiker spela samma truddilutt igen, men det är inte samma sak då! Ett musikstycke kan du spela upp igen och igen med exempelvis 24/192 och få fram exakt samma musikstycke, i princip (skivor pajar o.s.v., men principmässigt).
Så, vad är det för nytta med att ha en referens som man inte kan använda som referens mer än en gång?
Så tänker jag iaf. Det kanske är tokigt, vad vet jag, men jag tycker att en referens liknande DVD-A är logisk.
Samtidigt tycker jag att det funderas för mycket om vilket format som är bäst och så vidare. Vi nyttjar inte de befintliga formaten fullt ut, förutom i väldigt få fall. Varför ska vi då lägga pengar på nya format? Det är ju inte formatet som är problemet. Samtidigt, formatet öppnar ju för ännu bättre inspelningar, och detta till fler individer.
Nåja, det blir nog bra
Margaux skrev:En annan sak som slagit mig är att många som fått DVD-aha uppleveleser ofta fått det på högtalare som inte kan spela upp 96 k. Det vanliga för högtalare tills nyligen har varit upp till 25-30K.
Piotr skrev:Ledsen men tror inte 44.1k samplingsfrekvens kan inte fånga allt under 20k korrekt. Det är omöjligt. Topp oktaverna man hör på CD är kraftig distortion och vissa har svårt att vänja sig av med den.
För att med säkerhet kunna sampla en ren sinus vid 20k perfekt så krävs långt över två samples för varje period.
/Peter
IngOehman skrev:Den som vill få en mindre matematisk och mera grafiska förklaringar till hur samplingsteoremet interagerar med "verkligheten", kan läsa artikeln om digitalteknik i MoLt som publicerades någon gång alldeles i början av 90-talet. Jag tror det var 1991 någon gång? Den hette något i stil med:
'Sinken - lösningen till CD-systemets ekvation'
Men det finns fler argument. Tex argumentet att en spik kan gå snabbare än 20 k? Låt oss ta en perfekt fyrkantvåg. Den kan delas upp i ett antal sinustoner med varierande frekvens, tid och amplitud. Låt oss spela upp denna från DVD-Audio.
De har sina nollgenomgångar precis på de andra sampelplatserna, de där ringningarna bidrar också.Piotr skrev:Ringningarna man ser före/efter en impuls på CD, liger de i frekvens ovan hörbara spektrat?
Piotr skrev:Ringningarna man ser före/efter en impuls på CD, liger de i frekvens ovan hörbara spektrat?
Om man skulle sampla en enskild halv sinusperiod av 20k och återge den, skulle den också ha ringningar?
Piotr skrev:Ringningarna man ser före/efter en impuls på CD, liger de i frekvens ovan hörbara spektrat?
Piotr skrev:Jajjemensan,
samt att jag blir klokare och lär mig med en rasande takt.
Läste precis IÖ´s artikel så nu får jag komma upp med nya hemmasnickrade argument.
Blev fakstiskt lite klokare redan i går kväll/natt. Satt med papper och penna och skissade mig fram till att information "återskapas" korrekt även i tiden så länge man håller sig till Harrys regler dvs. 20k och därunder för Fs44.1.
Ringningarna man ser före/efter en impuls på CD, liger de i frekvens ovan hörbara spektrat?
Om man skulle sampla en enskild halv sinusperiod av 20k och återge den, skulle den också ha ringningar?
Kan det vara så att (som många föreslår) det är reduktion eller frånvaro av dessa ringningar som gör de nya formaten "bättre"?
Vi hör ju normalt inte enskilda signaler högre än 20k sisådär men örat/hjärnan har ju ändå en tidsupplösning som är mycket högre än så. Nere på mikrosekunder eller däromkring.
Svante skrev:Om kan däremot lyssnar på "ideala" lågpassfilter med lägre brytfrekvens (som ju då har ett impulssvar som ser ut som en sinc). så låter det väldigt "resonant" och de har dessutom en besvärande förringning. Det gör att det ideala lågpassfiltret inte alls är idealiskt till tex delningsfilter.
Har jag rätt eller har jag rätt?
IngOehman skrev:De ligger över, men de är inte "ringningar", utan det är faktiskt precis de signalfrekvenser som funnits i den analoga världen!
IngOehman skrev:Om man skulle sampla en enskild halv sinusperiod av 20k och återge den, skulle den också ha ringningar?
Det skulle den antingen inte eller också skulle den det!
Grejjen är den att det du beskriver är förbjudet. En enda period av en ton är nämligen mycket bradbandig och grundregeln är att det som samplas måste hålla sig under halva samplingsfekvensen.
IngOehman skrev:
Kanske dags för ett LTS-möte där ämnet blir "Hur tusan fungerar CD-systemet, egentligen?"...
Någon som tycker att ett sådant föredrag skulle vara intressant, så här 22 år efter systemts genomslag? (Jag höll ju ett sådant föredrag på 80-talet, men frågan kanske är aktuellt fortfarande? Det verkar ju som om många missförstånd lever kvar.)
IngOehman skrev:Kan det vara så att (som många föreslår) det är reduktion eller frånvaro av dessa ringningar som gör de nya formaten "bättre"?
Det finns inga ringningar. CD-systemet "adderar" ingenting till signalen på så vis, däremot finns det saker som fattas, brister - nämligen frekvenser över 22,05 kHz som är borttagna.
IngOehman skrev:Vi hör ju normalt inte enskilda signaler högre än 20k sisådär men örat/hjärnan har ju ändå en tidsupplösning som är mycket högre än så. Nere på mikrosekunder eller däromkring.
Tid och frekvens är inte samma sak, inte ens 1/frekvens är samma sak som tid eftersom "vad för något" fattas i ekvationen.
Du har helt rätt i att tidsupplösning och 1/periodtid för högsta frekvensen som hörs inte behöver vara samma sak dock, men så är också tidsupplösningen i CD-systemt EXTREMT mycket finare än en period, eller en halvperiod eller en hundradels period.
Läs artikeln igen!
Svante skrev:IngOehman skrev:De ligger över, men de är inte "ringningar", utan det är faktiskt precis de signalfrekvenser som funnits i den analoga världen!
Nu måste jag protestera, visst är det ringningar? Om man tar ett 2:a ordningens lågpassfilter med Q=10, visst ger det ringningar? Ringningar är ju just periodiskt gung på signalen i tidsdomänen. Visst, ringfrekvensen fanns i ursprungssignalen (i båda fallen), men det gör inte att det blir mindre ringning av det...
...Nja, jag tycker ju iofs att det är en intressant (om än felaktig) hypotes, eftersom man hör förringningar så tydligt vid lägre frekvenser.
Enda sättet att ta reda på det är genom lyssningstest, något som säkerligen har gjorts även om jag inte kan referera till nåt nu. Det är ju "bara" att ta en signal samplad med 192 kHz och bandbegränsa den till 22,05 med ett juste filter och blindtesta. Jag tror ingen kommer att höra det om testet görs rätt.
Mja, jag brukar översätta frekvens med "oftighet", så i den bemärkelsen är ju tid=1/frekvens, men visst är det så att en samplad signal kan ha högre tidsupplösning än sampelintervallet. Titta i artikeln på de samplade sincarna, de kan ju återskapas med toppen på godtycklig punkt emellan samplen. Tidsupplösningen är alltså oändlig, trots tidskvantiseringen!
IngOehman skrev:Svante skrev:IngOehman skrev:De ligger över, men de är inte "ringningar", utan det är faktiskt precis de signalfrekvenser som funnits i den analoga världen!
Nu måste jag protestera, visst är det ringningar? Om man tar ett 2:a ordningens lågpassfilter med Q=10, visst ger det ringningar? Ringningar är ju just periodiskt gung på signalen i tidsdomänen. Visst, ringfrekvensen fanns i ursprungssignalen (i båda fallen), men det gör inte att det blir mindre ringning av det...
Nej, jag håller inte med om att det är ringningar som CD-systemet visar, däremot är det givetvis det från det andra ordningens LP-filtret med Q=10. Men jag är medveten om att vetenskapliga världen i överigt inte skiljer på fenomenen.
Jag menar dock att en ringning är "det som hänger kvar efter att man anslagit ett resonant system"*. En kyrkklocka till exempel. Det är INTE vad det handlar om i CD-fallet. I själva verket är grupplöptiden noll vid 22,05 kHz när den är det vid 1 KHz eller 7 kHz. Det är inte en ringning, det är en vågning.
*Anslagit = tillfört energi
Olika ord för olika fenomen = bra idé.
IngOehman skrev:Jag tänkte inte prata i gbg (såvärst...) den här gången. Det är ju du som är stjärnan. Kör du, så kanske jag kör i Sth?
Svante skrev:IngOehman skrev:Jag tänkte inte prata i gbg (såvärst...) den här gången. Det är ju du som är stjärnan. Kör du, så kanske jag kör i Sth?
OK, jag fick intrycket att du skulle prata en av dagarna, synd.
Hotspur skrev:Svante skrev:IngOehman skrev:Jag tänkte inte prata i gbg (såvärst...) den här gången. Det är ju du som är stjärnan. Kör du, så kanske jag kör i Sth?
OK, jag fick intrycket att du skulle prata en av dagarna, synd.
Klubben för inbördes beundran? Det finns PM...
Morello skrev:Hotspur skrev:Svante skrev:IngOehman skrev:Jag tänkte inte prata i gbg (såvärst...) den här gången. Det är ju du som är stjärnan. Kör du, så kanske jag kör i Sth?
OK, jag fick intrycket att du skulle prata en av dagarna, synd.
Klubben för inbördes beundran? Det finns PM...
Svante skrev:Mja, fast det är ju samma fenomen... Tänk dig ett analogt hederligt tex 8:e ordningens butterworthlågpassfilter. Det har ringningar, beroende på att de ingående 2:a ordningens länkarna har ett Q>0,5, dvs de är underdämpade. Bygg nu vidare på butterworthfiltret till 1000:e ordningen, så kommer väldigt många av länkarna att bidra med ringningar. Enda olikheten jämfört med det ideala lågpassfiltret är nu fasgången, men tag då signalen och kör den öven baklänges genom samma filter, så blir det nollfas, dvs det ser ut som om signalen passerat genom ett nära nog idealt nollfaslågpassfilter. Med förringningar och allt. Och orsaken till detta är ringningarna i varje del av butterworthlågpassfiltret. Det här filtret blir väldigt likt det FIR-filter som typiskt sitter i en CD-spelare.
patrikf skrev:Hur är det här med "faslinjära högtalare" egentligen. Bara faslinjära längs en horisontal linje väl i detta fall?
IngOehman skrev:Svante skrev:Mja, fast det är ju samma fenomen...
Visst självklart, det är ju i princip samma sak. Ringningarna har tagits bort - genom att signalen har körts baklänges. Bra exempel! Tack.
IngOehman skrev:Hur är det förresten med delningsfilterfrågan, Svante? Du har inte svarat på mitt inlägg.
linjärfas-LP-brickwall + dito HP-brickwall, vad blir det...?
Vh, iö
Hotspur: jo visst beundrar jag IÖ för mycket, men jag försöker sätta dit honom när jag kan... Men PM, ja det kanske hade varit bättre. Det bara trillade in så naturligt i diskussionen som vi hade.
Hotspur skrev:Morello skrev:Hotspur skrev:Svante skrev:IngOehman skrev:Jag tänkte inte prata i gbg (såvärst...) den här gången. Det är ju du som är stjärnan. Kör du, så kanske jag kör i Sth?
OK, jag fick intrycket att du skulle prata en av dagarna, synd.
Klubben för inbördes beundran? Det finns PM...
Morello: Jag tolkar din "mad" som att du tycker att
LTS-egona tar alldeles för lite plats här på faktiskt,
eller?
IngOehman skrev:Svante:
1. Nä, det ringer inte alls! Ingen fördröjd energi. Ringer gör det i kyrkklockor. Vågning är ett mycket bättre ord för att beskriva nå't som syns på ett oscilloskop, men som man inte vet om det ringer eller vägar sig av andra skäl, än.
IngOehman skrev:2. Elementen skall förstås vara, våglängdsräknat, nära varandra.
Men helt bortsett ifrån detta är DVD-A överlägset de båda andra alternativen
Men, vore det omöjliga möjligt, dvs att elementen sutte i samma punkt, så skulle det bli perfa.
patrikf skrev:Svante skrev:Men, vore det omöjliga möjligt, dvs att elementen sutte i samma punkt, så skulle det bli perfa.
Men det är väl inte omöjligt? Du menar väl gemensamt akustiskt centrum?
Svante skrev:patrikf skrev:Svante skrev:Men, vore det omöjliga möjligt, dvs att elementen sutte i samma punkt, så skulle det bli perfa.
Men det är väl inte omöjligt? Du menar väl gemensamt akustiskt centrum?
Jag vet faktiskt inte... Jag antar att du tänker dig ett litet diskantelement mitt i ett större baselement. Baselementet som ringradiator...Mja, kanske det skulle funka, men lite knepigt blir det att flura ut hur de olika bidragen från baselementets kon läggs ihop med diskantelementets. Hursomhelst så krävs det oerhört lite löptidsskillnad för att ringningarna
ska höras.
Svante skrev:Jag vill påstå att detta är omöjligt. Säg att vi lyckas få diskantelementets akustiska centrum 3,45 cm ifrån baselementets. Säg också att vi delar vid 1 kHz. Filtrets svansar kommer att ringa med frekvensen 1 kHz, dvs våglängden för ringningen är 345/1000=34,5 cm. Vi kommer i riktning rakt uppåt att få summan av två dämpade sinusar (sincsvansen) i motfas, men den ena fördröjd 1/10 period. I runda slängar får resultatet en amplitud på 1/10 av var och en av de två motfasiga sincarna, dvs 20 dB ner. En förringning 20 dB ner kommer alla gånger att höras. Än värre blir det med realistiska mått och delningsfrekvenser...
IngOehman skrev:Svante skrev:Jag vill påstå att detta är omöjligt.
Är det en naturlag att det måste handla om en delning vid några kHz mellan ett diskantelement och något därunder?
Ibland delar man vid lägre frekvenser.
IngOehman skrev:
Energin är inte utdragen i tiden. Det bara ser så ut.Man skall inte tro på oscilloskopsbilder annat än... när det är lämpligt att göra det.

De spektrala komponenternas utbredning i tidsdomän är nämligen större än pulsens bredd, redan från början, det är bara det att det inte syns när pulsen ser kort ut.
Detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
IngOehman skrev:
Vh, Ing. Öhman
PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
IngOehman skrev:Nä.
Svante skrev:Åkejrå, jag kanske får ge mig där.
Svante skrev:Men hursomhelst så är det lite skillnad på detta och det vanliga "liten i förhållande till våglängden", eftersom det är det lilla som blir kvar efter skillnadssignalsbildningen som är viktigt. 3,44 meter och 3,44 cm isär ger fortfarande 1/100 kvar vilket är 40 dB ner.
Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
dawen skrev:Används det här elementet i någon Inokonstruktion man känner till? Det låter onekligen som ett intressant element.
De spektrala komponenternas utbredning i tidsdomän är nämligen större än pulsens bredd, redan från början, det är bara det att det inte syns när pulsen ser kort ut.
IngOehman skrev:Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Det har jag inte gjort. Jag spekulerar bara. Nollhypotesen är en bra utgångspunkt dock, i många vetenskapliga frågeställningssammanhang, tycker du inte?
Ingen av oss lär kunna bevisa att det inte går att höra vågningen off axis, men kanske någon av oss kan visa att det går? Exempelvis den som tror att det går...
IngOehman skrev:Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Nu blir jag stum igen. För ett ögonblick.

Nu, när stumheten gått över frågar jag mig (och dig) denna humanistiska (krusfria) fråga:
Hur kan ett system som påstås vara linjärt och ringande, släppa igenom en signal utan att påverka den, trots att signalen ifråga har en bandbredd lika stor som systemts bandbredd?
Rätt svar: Det kan det inte! Således: Systemet ringer tydligen inte.
IngOehman skrev:Sen är jag den förste att erkänna att den vetenskapliga världen (av idag) bryr sig inte om att distingera mellan orsakerna till vågning, utan kallar allt ringning. Jag gör det inte dock, och kommer inte börja göra det idag heller.
[/size]
IngOehman skrev:Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
Spekulation: Då tror jag att det var ett försök med bara ett LP- eller ett HP-filter, och inte summan av de två?
IngOehman skrev:
Alla branta filter låter nämligen som om de ringer när de inte sällskapas av sin andra hälft.
IngOehman skrev:Det beror på att de har ett "vasst knä" sedda ensamma. Knäets frekvens tillåts dominera över sina kringliggande frekvenser.
Piotr skrev:IÖ skrev;De spektrala komponenternas utbredning i tidsdomän är nämligen större än pulsens bredd, redan från början, det är bara det att det inte syns när pulsen ser kort ut.
Tror jag nosat på det här förut, skall se om jag hänger med.
En puls innehåller "samtliga" frekvenser pga, oändlig bandbredd men dock under en kort begränsad tid.
Impulsen kan inte se ut som den gör utan högfekvens innehåll, utan skulle då se annorlunda ut och viktigast av allt, den mer lågfrekventa energin i pulsen har i själva verket startat tidigare än vad det ser ut som med HF innehållet?
Tror jag kanske förstår men vet inte om jag förklarar mig vidare bra..
/Peter
Svante skrev:IngOehman skrev:Svante skrev:Jag skulle fortfarande inte förvånas om inringningen går att höra (om vi fortfarande pratar om ett "idealt" lågpass/högpassfilter. Men har du gjort experimentet så får jag tro på det.
Det har jag inte gjort. Jag spekulerar bara. Nollhypotesen är en bra utgångspunkt dock, i många vetenskapliga frågeställningssammanhang, tycker du inte?
Ingen av oss lär kunna bevisa att det inte går att höra vågningen off axis, men kanske någon av oss kan visa att det går? Exempelvis den som tror att det går...
Ja, det är ju det jag brukar säga till de som hör saker som inte jag tror på. Man kan ju tänka sig en simulering här faktiskt, att man tar en hög- och en lågpassgren och fördröjer den ena i datorn och ser om det hörs någon ringning. Fast, förstås blir det svårt att skilja från en eventuell tonkurveavvikelse, eller så är det bara ett dumt försök att skilja två begrepp från varandra (tonkurva/ringning) mha ett lyssningstest, det kanske inte går. Hmm.
Svante skrev:IngOehman skrev:Svante skrev:IngOehman skrev:...detta kan man lätt undersöka genom att kolla hur en Sinc förvrängs i tidsdomän när man kör den genom att brickwallsystem... vars... överförningsfunktion definieras av en likadan sink för filtertermerna!
Svar: Den ändrar sig inte överhufvudtaget!
Ingen utdragning i tidsdimensionen (ringning) sålunda för det spektrum som hanterats! Detta behöver inte bevisas så länge vi är öfverens om att det är linjära system vi talar om.
Det är vi nog.
Jadå, det är vi överens om, linjärt ska det vara. Vad vi inte är överens om att man kan hoppa mellan tids- och frekvensdomänen så där....
...Men... Du har en poäng i det där med att köra en sinc genom lågpassfiltret, den blir inte utsmetad i tiden på samma sätt som impulsen.
Nu blir jag stum igen. För ett ögonblick.

Nu, när stumheten gått över frågar jag mig (och dig) denna humanistiska (krusfria) fråga:
Hur kan ett system som påstås vara linjärt och ringande, släppa igenom en signal utan att påverka den, trots att signalen ifråga har en bandbredd lika stor som systemts bandbredd?
Rätt svar: Det kan det inte! Således: Systemet ringer tydligen inte.
Jomen... Förklaringen ligger ju hoppandet mellan tids- och frekvensdomän... Ringning definieras i min värld i tidsdomänen. Det är ett utklingningsförlopp i tidsled. Tittar vi på tidssignalen så har den in- och utringning (urringning?).
Svante skrev:Om vi i stället väljer att titta i frekvensdomänen så kan vi inte tala om in- och utringning, eftersom ringning är ett begrepp som förklarar hur signalen beter sig i tidsled.
Svante skrev:Jag kan kontra med ett motexempel, tag det där 2:a ordningens lågpassfiltret med Q=10 och f0=1000 Hz. Kör in en sinc, bandbegränsad till 10 Hz. Ringer det nu? Knappast, signalen ser i det närmaste identisk ut med det vi stoppade in.
Svante skrev:Kan man av detta dra slutsatsen att ett sådant filter inte ringer?
Svante skrev:(nej insignalen har inte samma bandbredd som systemet, men varför ska vi ha just den begränsningen, som är i frekvensdomänen, när vi undersöker tidsförlopp).
Svante skrev:IngOehman skrev:Sen är jag den förste att erkänna, att den vetenskapliga världen (av idag) bryr sig inte om att distingera mellan orsakerna till vågning, utan kallar allt ringning. Jag gör det inte dock, och kommer inte börja göra det idag heller!
[/size]
Nja, det är ju en lite tråkig inställning, att inte vara beredd att ompröva sin tro. Det är tur att det står "idag" där, vi får väl hoppas på "i morgon", då.
Svante skrev:iö skrev:Svante skrev:iö skrev:PS. Är du verkligen alldeles säker på att du, i ditt exempel, skulle höra förvågningssvansen?
Jag är inte säker...
Den höga delningsfrekvensen du utgår ifrån gör faktiskt svansen rätt så kort, dessutom genereras den bara off axis, och kommer att sålunda att anlända primärt i form av reflekterat ljud, så före direktljudet kommer den inte att anlända dina hörorgan.
Nja, jag har ju inte provat, förstås. Men Lilltroll som gjorde exjobb på digitala delningsfilter (som jag lyssnade lite hastigt på och tyckte att det ringde) menar i rapporten att det "ideala" filtret inte alls är det ideala. Eller hur Lilltroll (om du läser).
Spekulation: Då tror jag att det var ett försök med bara ett LP- eller ett HP-filter, och inte summan av de två?
Nix! Det var ett delningsfilter, dvs med både bas- och diskantkanal. Det var inklusive högtalarelement och rum, och det är klart att man kan kritisera elementen och säga att de inte var tillräckligt bra, och att ringningen hördes därför. Å andra sidan är det ju meningen att man ska kunna använda delningsfilter till just högtalare.
Svante skrev:IngOehman skrev:Alla branta filter låter nämligen som om de ringer när de inte sällskapas av sin andra hälft.
Jajustdet, och om inte elementen eller de rumsliga egenskaperna tillåter utsläckning av ringningarna, så kommer det att bli en rest kvar som i princip kan höras.
Svante skrev:Vad jag menar är att det är ganska noga med detta, dels får inte elementen sitta långt ifrån varandra och då talar vi om 1/10 våglängd eller nåt, dels får inte elementens tonkurva avvika från det planerade med mer än 0,8 dB om 1/10 ska vara uppfyllt.
Svante skrev:IngOehman skrev:Det beror på att de har ett "vasst knä" sedda ensamma. Knäets frekvens tillåts dominera över sina kringliggande frekvenser.
Ja, det där är ju ett synsätt.
Svante skrev:Ett annat skulle vara att örat faktiskt analyserar tidssnuttar av signalen, ungefär som ett spektrogram. En sån där omatematisk processning påhittat av en pragmatisk evolution. Om impulssvaret blir för utbrett i tiden, så spiller ringningen över i ett perceptuellt särskiljt tidsintervall, och då hör vi en ton.
Svante skrev:Det kan illustreras genom att ta sig en sinc (som den jag länkade till tidigare i tråden) och göra en FFT på en snutt före själva toppen. Eftersom örat gör något som liknar detta är det inte konstigt att vi hör en frekvens (ringningens, som "råkar" sammanfalla med knäet).
Vilket synsätt som är "rätt" kan vi nog diskutera i evighet.
IngOehman skrev:...
IngOehman skrev:För mig är ringning den fördröjda energiavlämning
som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats.
Morello skrev:Nu tror jag IÖ våldförde sig på definitionen av periodisk eller också var det bara ett stavfel.
Svante skrev:IngOehman skrev:För mig är ringning den fördröjda energiavlämning
som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats.
OK då, om vi nu tar en impuls, när avlämnar den sin energi? Jo vid ögonblicket för impulsen. Så får den passera genom ett brickwallfilter (som iofs är icke-kausalt, men strunta i det nu).
När avger sincen som kommer ur det sin energi? Jo efter och före (ochpå) tidpunkten för impulsen. Ett brickwallfilter har alltså både för- och efterringning.
Svante skrev:Visst, om vi exciterar filtret med en signal som inte framkallar ytterligare ringning, som en sinc, så ser vi inte ringningarna från filtret. Det gör vi inte heller i fallet med lågpasslänken (Q=10 f0=1000, exciterad av 10Hz-sinc) Men om vi exciterar filtret med en signal med frekvenser över f0 för brickwallfiltret, så syns de.
IngOehman skrev:Morello skrev:Nu tror jag IÖ våldförde sig på definitionen av periodisk eller också var det bara ett stavfel.


Förklara dig.
Vh, Ing. Öhman
IngOehman skrev:
Ser man på förloppet I TIDSDOMÄN, men sönderdelat i frekvensavsnitt, så ser man emellertid att respektive frekvensband inom hela CD-registret är HELT OSKADAT i tidsdomän.
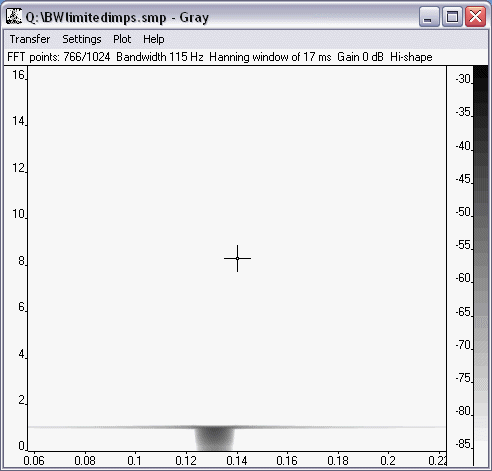
IngOehman skrev:
Nä, typ alla signaler som håller sig under 22 050 Hz. Då syns bara (i förekommande fall) vågningar från den högsta (men fortfarande icke-tidsfördröjda) signalkomponenten. Det betyder att: CD-SYSTEMET SAKNAR RINGNINGAR INOM FREKVENSOMRÅDET 0 - 22 050 Hz!

Och det är trevligt!
Det skall vi vara glada över, och kanske till och med hoppa och skutta runt lite glatt (tjoa är också ok) om vi känner att vi måste. Det tycker jag är rimligt.
Tjohopp!
Vh, Ing. Öhman
markih skrev:Jag tycker rent intuitivt att IÖ har rätt i det att betydelsen av ordet ringning är kausalt
Om jag har läst rätt, jag har bara skummat väldigt snabbt, för ordväxlingen är verkligen utförlig

Dvs för-ringning är ett begrepp utan intuitiv och praktisk (i verkligheten fysikalisk) förankring. För-ringning kanske passar som ett matematiskt begrepp?
dimitri skrev:Svante,
Du visar en signal på 115 HZ och ett tidsfönster på 17 ms.

IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Svante skrev:Lilltroll: såg du morellos definition av periodiska signaler? Jag vet inte om jag instämmer helt i den, jag tycker nog också att en avklingande signal kan vara periodisk, men känner mig ingalunda säker på terminologin.
Martin skrev:Alltså säg en oändlig serie av korta pulser i tidsdomänen är väl periodisk? Då kan man väl tänka sig att en sådan serie med för-och eftervågningar vid varje puls också är helt periodisk, även enligt "Morellos" definition?
lilltroll skrev:IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Här håller jag inte med.
Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet. Har vi många poler får vi en överlagring av många ringningar, med det är summan av ett antal periodiska ringningar. Sedan tillkommer en avklingningsfaktor på hela svaret med den korrelerar till det reela värdet på polplaceringen. Jag är medveten om att en AM-modulering av en signal påverkar frekvensinnehållet, men gör man ovanstående separation, så blir den kvarvarande ringningen periodisk.
lilltroll skrev:Svante skrev:Lilltroll: såg du morellos definition av periodiska signaler? Jag vet inte om jag instämmer helt i den, jag tycker nog också att en avklingande signal kan vara periodisk, men känner mig ingalunda säker på terminologin.
Avklingningen (omm LTI) kan skrivas som produkten mellan två exp. serier, på den allmänna formen e^At*e^jBt
e^jBt är periodisk.
Svante skrev:Lilltroll: såg du morellos definition av periodiska signaler? Jag vet inte om jag instämmer helt i den, jag tycker nog också att en avklingande signal kan vara periodisk, men känner mig ingalunda säker på terminologin.
Svante skrev:Smisk på dig, jag har ju sagt att du inte får hoppa sådär. Antingen frekvens eller tid har jag ju sagt!
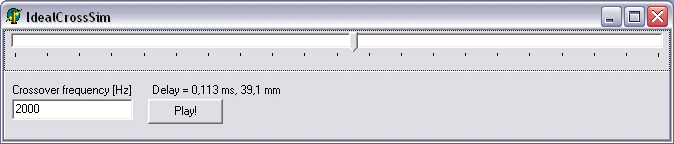
Svante skrev:Men åkejrå, om vi nu trots allt hoppar lite och gör ett spektrogram på en sinc, så blir det så här:
(Se bilden i original-postningen långt ovan)
dvs för- och efterringningen syns tydligt vid f0 för sincen (1000Hz).
Svante skrev:Javisst, där är jag nästan helt med. En CD-sinc ringer vid 22050 Hz, men inte därunder. Och CD är kanon, ifall nu någon trodde att jag menade nåt annat.
IngOehman skrev:Morello!
Läs "...som ett resonant system (icke-aperiodiskt) uppvisar efter..." så många gånger du behöver för att inse syftningen!
Om du fortfarande är osäker, läs originalinlägget ett par meningar ytterligare. Sen kan du få min tillåtelse att posta en
Vh, Ing. Öhman
lilltroll skrev:IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Här håller jag inte med.
lilltroll skrev:Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet.
Har vi många poler får vi en överlagring av många ringningar, med det är summan av ett antal periodiska ringningar. Sedan tillkommer en avklingningsfaktor på hela svaret med den korrelerar till det reela värdet på polplaceringen. Jag är medveten om att en AM-modulering av en signal påverkar frekvensinnehållet, men gör man ovanstående separation, så blir den kvarvarande ringningen periodisk.
lilltroll skrev:Om vi börjar med att titta på definitioner av vedertagna engelska begrepp.
The Gibbs phenomenon is an overshoot (or "ringing") of Fourier series and other eigenfunction series occurring at simple discontinuities.
ref: http://mathworld.wolfram.com/GibbsPhenomenon.html
Summary: The Fourier Series is the representation of continuous-time, periodic signals in terms of complex exponentials. The Dirichlet conditions suggest that discontinuous signals may have a Fourier Series representation so long as there are a finite number of discontinuities. This seems counter-intuitive, however, as complex exponentials are continuous functions. It does not seem possible to exactly reconstruct a discontinuous function from a set of continuous ones. In fact, it is not. However, it can be if we relax the condition of exactly and replace it with the idea of almost everywhere. This is to say that the reconstruction is exactly the same as the original signal except at a finite number of points. These points, not necessarily suprisingly, occur at the points of discontinuities.
ref: http://cnx.rice.edu/content/m10092/latest/
Steg 1:
Är alla inblandade överens om att det ovan är korrekt?
Morello skrev:lilltroll skrev:IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Här håller jag inte med.
Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet. Har vi många poler får vi en överlagring av många ringningar, med det är summan av ett antal periodiska ringningar. Sedan tillkommer en avklingningsfaktor på hela svaret med den korrelerar till det reela värdet på polplaceringen. Jag är medveten om att en AM-modulering av en signal påverkar frekvensinnehållet, men gör man ovanstående separation, så blir den kvarvarande ringningen periodisk.
Å andra sidan får vi inte ett periodiskt svar om vi med impuls exciterar ett system där polernas realdel är mindre än noll.Vi får svängande termer som avklingar och polernas realdel(sigma) återfinnes, efter transformering till tidsplanet, i den avtagande funktionens exponent.
Periodiskt svar får vi om och endast om polernas realdel är exakt noll, dvs polerna ligger på imaginära axeln i s-planet.
Svante skrev:... Ja döm själva! Ringer det?
IngOehman skrev:lilltroll skrev:IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Här håller jag inte med.
Det är inte fråga om att hålla med eller inte hålla med. Det är ett faktum att en ringning för mig är "den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats".
Kontrollfråga:
Om du säger "Jag tycker att choklad är gott", kan jag inte rimligen säga: "Här håller jag inte med"! Eller hur?
Jag har ju inte ätit choklad med din mun. lilltroll skrev:Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet.
lilltroll skrev:Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet.
Du gör axiom av det faktum att ett periodiskt svar ÄR en ringning. Men det var ju just det vi höll på att diskutera. Då kan man inte bevisa att det är det, bara genom att påstå att det är det. Frågan är, varför anser man att en vågning behöver vara en ringning? Är en sinuston enligt din mening också en ringning?Har vi många poler får vi en överlagring av många ringningar, med det är summan av ett antal periodiska ringningar. Sedan tillkommer en avklingningsfaktor på hela svaret med den korrelerar till det reela värdet på polplaceringen. Jag är medveten om att en AM-modulering av en signal påverkar frekvensinnehållet, men gör man ovanstående separation, så blir den kvarvarande ringningen periodisk.
En ringning, liksom en vågning, är alltid periodisk (om man använder den generösa definitionen, jfr Morellos inlägg), med det betyder inte att en periodisk signal är en ringning.
Hänger du med?
En högtalare ger ifrån sig ljud, men det gör inte alla saker som låter till högtalare.
Vh, iö
PS.
IngOehman skrev:Man kan för övrigt diskutera vad man menar med "exakt rekonstruktion". Tillåts limes-beräkningar tillträde i kombination med lite modifierade algoritmer blir Bibbs-phenomenon-sanningen tveksam.
lilltroll skrev:IngOehman skrev:lilltroll skrev:IngOehman skrev:Har en egen teori om varför vi inte når koncensus:
Tror inte vi är överens om själva begreppet ringning. That's all!
För mig är ringning den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats. Själva avklingningen kan dock vara aperiodisk.
Vh, iö
Här håller jag inte med.
Det är inte fråga om att hålla med eller inte hålla med. Det är ett faktum att en ringning för mig är "den fördröjda energiavlämning som ett resonant system (icke-aperiodiskt) uppvisar efter att det har exiterats".
Kontrollfråga:
Om du säger "Jag tycker att choklad är gott", kan jag inte rimligen säga: "Här håller jag inte med"! Eller hur?
Jag har ju inte ätit choklad med din mun. lilltroll skrev:Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet.
lilltroll skrev:Om vi exiterar ett LTI system, där överföringsfunktionen är konstant under exitationsfasen, så kommer man se periodiska svar. Frekvensen för ringningen återfinns i det imaginära värdet för polplaceringen i Laplace-planet.
Du gör axiom av det faktum att ett periodiskt svar ÄR en ringning. Men det var ju just det vi höll på att diskutera. Då kan man inte bevisa att det är det, bara genom att påstå att det är det. Frågan är, varför anser man att en vågning behöver vara en ringning? Är en sinuston enligt din mening också en ringning?Har vi många poler får vi en överlagring av många ringningar, med det är summan av ett antal periodiska ringningar. Sedan tillkommer en avklingningsfaktor på hela svaret med den korrelerar till det reela värdet på polplaceringen. Jag är medveten om att en AM-modulering av en signal påverkar frekvensinnehållet, men gör man ovanstående separation, så blir den kvarvarande ringningen periodisk.
En ringning, liksom en vågning, är alltid periodisk (om man använder den generösa definitionen, jfr Morellos inlägg), med det betyder inte att en periodisk signal är en ringning.
Hänger du med?
En högtalare ger ifrån sig ljud, men det gör inte alla saker som låter till högtalare.
Vh, iö
PS.
1. Jag syftar på ditt påstående:
Själva avklingningen kan dock vara aperiodisk
lilltroll skrev:2. Jag anser inte att ett system som har alla poler på jw-axeln behöver en annan uppsättning definitioner än ett system där vi flyttar några av polerna ut från jw-axeln. Om vi har ett system i vila, med polerna på jw-axeln, som vi sedan exiterar så anser jag att resultatet är en ringning.
lilltroll skrev:Råkar vi flytta någon pol åt höger så har vi fortfarande en ringning, men systemet är inte BIBO-stabilt.
lilltroll skrev:IngOehman skrev:Man kan för övrigt diskutera vad man menar med "exakt rekonstruktion". Tillåts limes-beräkningar tillträde i kombination med lite modifierade algoritmer blir Gibbs-phenomenon-sanningen tveksam.
Antingen anser du att Bibbs-phenomen är korrekt, annars anser du att det är felaktigt. Inga mellanting.
Anser du att det är korrekt eller fel?
IngOehman skrev:Menar du att ett resonant system alltid måste ringa när det exiteras, oavsett om det exiteras med en insignal som passerat säg ett system med nollställen på alla de platser där det undersökta systemet har poler?
IngOehman skrev:Svante skrev:... Ja döm själva! Ringer det?
Nej, det ringer inte, men piper gör det.
IngOehman skrev:Nämenokejdå...
Det ringer.
Om det måste heta så för att alla skall bli nöjda ger jag mig.
Inte för att det är rimligt, utan för att jag tror på principen att alla skall tala samma språk om de vill förstå varandra.
Min point var bara att det är en bra grej att med ord skilja på saker som är olika. Om det är allas önskan att kalla allt för ringningar så får vi väl göra så då.
Vh, iö (Demokrat???)
IngOehman skrev:Det gläder mig!
Är alla de andra sakerna ringningar då?
Vh, iö
IngOehman skrev:Lilltroll:
Jag har absolut inte påstått att det jag ville införa var vedertagna begrepp - raka motsatsen. Jag säger bara att de är bättre än vedertagna begrepp, eftersom de ger bättre entydlighet.
Men strunt samma. Ni får som ni vill, stagnation är tillåtet.
Vh, iö
Svante skrev:IÖ: Kompis igen?
Martin skrev:jag måste bara säga att jag håller med IÖ faktiskt, även med min ytliga kunskap. Ringning kanske inte är rätt ord eftersom det bara är en konsekvens av att man tar bort frekvenser från en (egentligen) periodisk signal. Säg en fyrkantvåg (eller pulståg) som man tar bort allt över en viss frekvens. Ringer den då? De lägre frekvenserna "ser" ju exakt likadana ut som innan.
Naqref skrev:
Precis vad jag tycker oxå! Ringningarna är en konsekvens av brist på övertoner och är inget som påminner om ringningar i den erfarenhetsmässiga praktiska verkligheten. Vågningar är bättre ord. Kanske vi borde ha en omröstning?
lilltroll skrev:
Går det att beskriva och definiera de olika begreppen på max ca 10 rader, helt torrt och vetenskapligt utan eget tyckande sarkasmer eller smilies?
Margaux skrev:
Faktum.se när den är som bäst!
hrrmm... ?
IngOehman skrev:Så, det står fortfarande 1 - 0.
Harryup skrev:Kan det finnas en poäng med att ha ett gemensamt språk med andra och inte uppfinna egna nya namn utan att först kontrollerat källor till hur det benämns av andra verksamma inom området, dvs icke-faktisianer?
mvh/Harryup
Svante skrev:Det här var en gammal tråd, ganska bra var den också.
Jag tycker INTE att man ska ha olika namn för de två fenomenen eftersom de inte går att skilja åt med en tydlig skiljelinje.
Svante skrev:Exempel:
Om man tar ett brant kausalt lågpassfilter och kör en impuls genom det, så skulle signalen få ringingar enligt både min IÖs definition. Kör man sedan signalen ytterligare en gång fast baklänges genom filtret så skulle signalen få förringningar. Om filtret är superbrant (brickwall, men inte nödvändigtvis nollfas) så har man fått en sinc. Och den har då vågningar men inte ringningar?
Svante skrev:Det som uppenbart har varit ringningar åt de båda hållen ska nu alltså kallas vågningar?
Svante skrev:Nä. Att sincens ringningar verkar vara något väsensskilt från ringningar är bara beroende på att IÖ väljer ett annat betraktelsesätt för just den signalen. Väljer man att se den som jag gör ovan som två filteringar (fram- och baklänges) genom ett kausalt brickwallfilter så är det uppenbart att begreppet ringningar passar även då.



Naqref skrev:IngOehman skrev:Den som vill få en mindre matematisk och mera grafiska förklaringar till hur samplingsteoremet interagerar med "verkligheten", kan läsa artikeln om digitalteknik i MoLt som publicerades någon gång alldeles i början av 90-talet. Jag tror det var 1991 någon gång? Den hette något i stil med:
'Sinken - lösningen till CD-systemets ekvation'
Du menar denna?
http://www.lts.a.se/artiklar/sincen.pdf
Användare som besöker denna kategori: Kalejdokom och 16 gäster